Дані по прибутковості фінансового ринку та акцій тов “Турбоатом” за певний період

Період	03.01-10.01	11.01-17.01	18.01-24.01	25.01-01.02	01.02-07.02	08.02-14.02	14.02-21.02
F	14	15	16	15	15	16	17
x 5	8	9	7	6	6	7	9

Рис. 3.5. Зміна прибутковості фінансового ринку за рахунок зміни прибутковості акцій Турбоатом

Регресія d на f має вигляд: d = 0,1765f + 14,119. Отже, випадкова величина залишкових коливань е є d – 0,1765f – 14,119. Знайдемо варіації залишків, склавши низку значень е (табл. 3.10):

Таблиця 3.10

Варіації залишкових коливань курсу цінних паперів тов “Турбоатома”

03.01-10.01	11.01-17.01	18.01-24.01	25.01-01.02	01.02-07.02	08.02-14.02	14.02-21.02
-2	-1	1	0	0	1	1

Середнє, природно, дорівнює 0, і тому = 0,77. Далі, = b = 0,176, = 0,176*0,82/0,77=0,187, = - 1,539.

Ефективність цінних паперів зручно відраховувати від ефективності без ризикового вкладу . Отже, m_i = a_i + β_i m_f = m₀ + β_i(m_f – m₀) + α_i де

α_i=a_i+(β_i-1)m₀. Перевищення ефективності цінного паперу над безризиковою ефективністю m₀ називається премією за ризик. Таким чином, ця премія за ризик в основному лінійно залежить від премії за ризик, що складається для ринку в цілому, і коефіцієнтом є “бета” даного паперу. Це, однак, вірно, якщо = 0. такі цінні папери називаються “справедливо” оціненими. Ті ж папери, у яких > 0, ринком недооцінені, а якщо < 0, то ринком переоцінені.

Розрахувавши для всіх цінних паперів коефіцієнти , можна зробити наступний висновок: акції Центренерго і Турбоатому переоцінені ринком, а цінні папери інших підприємств, навпаки, недооцінені. Отже, необхідно купувати акції TOB “Дніпроенерго”, TOB “Київенерго” та TOB “Укртатнафти”.

Розглянемо в цій ситуації портфель цінних паперів. Виявляється, ефективність ризиковій частині портфеля з зафіксованими частками також лінійно залежить від ефективності фінансового ринку. Справді, нехай частка i – тієї цінного паперу є x_i , тоді ефективність портфеля:

(3.4)

або, позначивши

отримаємо .

Дисперсія розглянутого портфеля: може бути розбита на дві частини:

(3.5)

Оскільки перша частина являє зважену суму власних дисперсій доходностей паперів, що входять у портфель, то ця частина може бути названа власної дисперсією портфеля, а квадратний корінь з неї, тобто може

бути названий власним ризиком портфеля. Друга частина повинна бути названа ринкової дисперсією:

Отримуючи з неї квадратний корінь, одержуємо ринковий ризик портфеля:

Задачу Марковіц про формування портфеля заданої ефективності та

мінімального ризику тепер можна сформулювати так:

∑ x_i ( a_i + b_im_f) = m_p (3.6)

Вирішуючи завдання за допомогою табличного процесора Excel і його надбудови Пошук рішення, отримаємо: rp= 1,33 х 1 = 0; х 2 = 0,45; х 3 = 0; х 4 = 0,53; х 5 = 0,02.

ap = 11,96 + (0,58-1) * 19 = 3,98, тобто портфель недооцінений ринком.

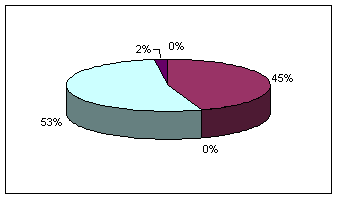Рис. 3.6. Оптимальний портфель Марковіца мінімального ризику з

урахуванням фінансового ринку

Задачу Марковіца про формування портфеля максимальної

ефективності і заданого ризику тепер можна сформулювати так:

∑x_i ( a_i + b_im_f) → max

(3.7)

Вирішуючи завдання за допомогою табличного процесора Excel і його надбудови Пошук рішення, отримаємо:

m_p= 26,21 х ₁ = 0,29; х ₂ = 0; х ₃ = 0; х ₄ = 0,71; х ₅ = 0. _p = 11,54 + (0,6-1) * 19 = 3,94, тобто портфель недооцінений ринком.

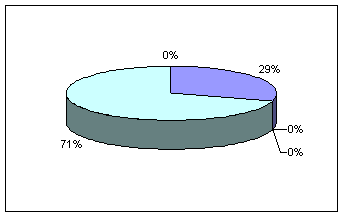Рис. 3.7. Оптимальний портфель Марковіца максимальної ефективності

Не тільки цінні папери мають “бети”, а й портфелі, і “бета” портфеля

дорівнює зваженої сумі “бета” паперів, що входять у портфель. Подібним чином “альфа” портфеля дорівнює a_p + (β_p – 1) m₀ . Як і для паперів, портфель називається “справедливо” оціненим, недооціненим, переоціненим, якщо відповідно a_p = 0, a_p > 0, a_p < 0.

Необхідно вибрати такий оптимальний портфель цінних паперів, який задовольняв би двома показниками:

- ефективність портфеля не менше 8%; - ризик портфеля не більше 0,71%.