1. Електрофізичні основи схемотехніки

1.1 Лінійні перетворення електричних сигналів у

радіоелектронних пристроях

1.1.1 Підсилювальні пристрої електричних сигналів

Ряд радіоелектронних систем та пристроїв характеризуються тим, що в

їх структурі можна виділити вхід, призначений для подачі сигналів, і вихід,

звідки перетворені сигнали поступають для подальшого їх використання.

Такий підхід до перетворень сигналів можна проілюструвати за допомогою

”чорної скриньки” (рис. 1.1)

Рис. 1.1. Макромодель радіоелектронного пристрою – ”чорна скринька”

Тоді

U

 KU ,

вих

вх

де U вх – величина вхідного сигналу(збурення); U вих – величина

вхідного сигналу(реакції системи або її відгук); K – системний оператор.

Базовим елементом лінійних перетворень електричних сигналів є

підсилювач

електричних

сигналів,

зібраний

на

дискретних

елементах(транзисторах чи електронних лампах), або в інтегральному

виконанні(операційний підсилювач).

Загалом, підсилювач призначений для збільшення(підсилення)

потужності електричного сигналу за рахунок енергії джерела живлення.

Підсилення здійснюється за допомогою керованих елементів(транзисторів,

тощо). Структурна схема пристрою підсилення сигналу зображена на рис.

1.2.

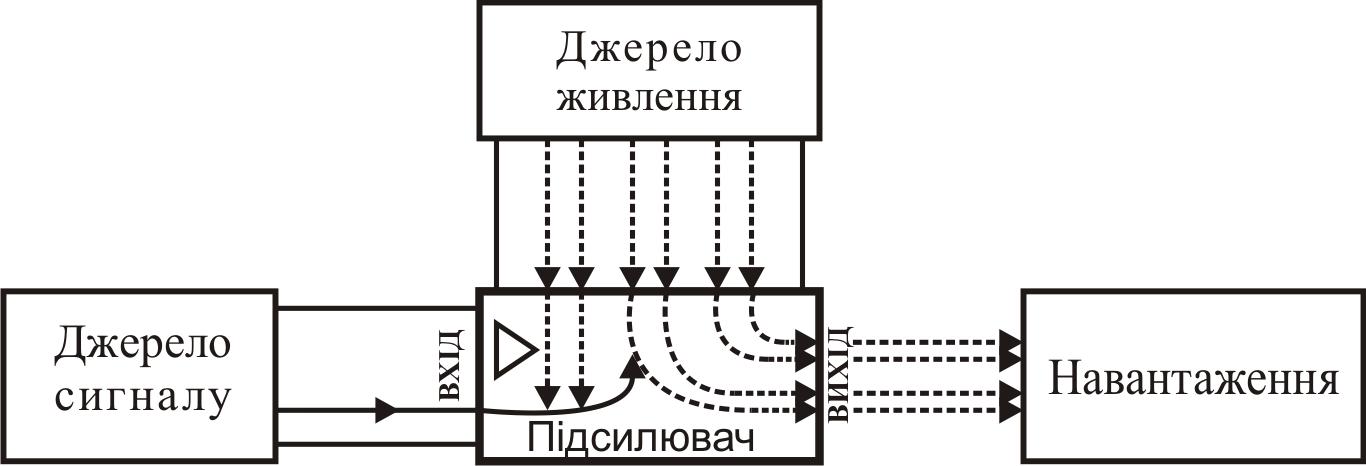
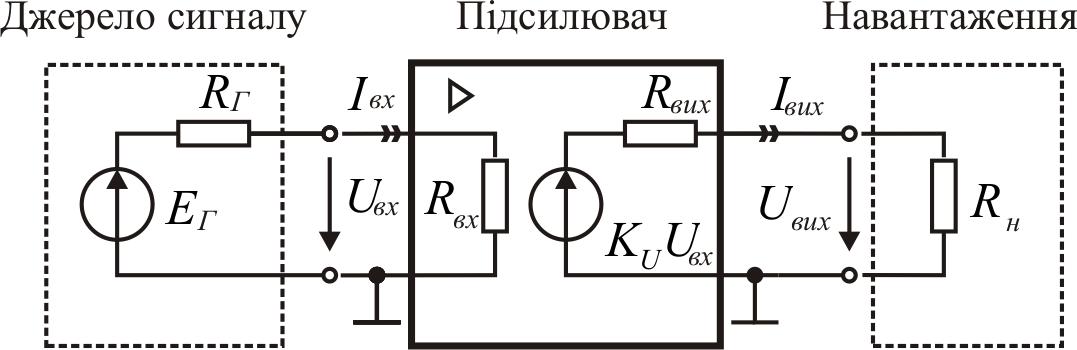
Рис. 1.2. Взаємодія підсилювача із зовнішніми пристроями

Тобто, підсилювач – це перетворювач енергії джерела живлення в

потік енергії, що поступає в навантаження, а величиною цього потоку керує

вхідний сигнал.

Джерелом вхідного сигналу може бути: мікрофон, фотоелемент,

термопара, попередній підсилювач, тощо.

Споживачем або навантаженням може бути: телефон, гучномовець,

гальванометр, осцилограф, реле, резистор, наступний підсилювач, тощо.

1.1.2 Основні показники підсилювальних пристроїв

Показники підсилювального пристрою – це параметри і

характеристики, що дають можливість оцінити підсилювач як

радіоелектронний пристрій для перетворення сигналу. Вони нічого не

говорять про схему підсилювача або процеси, що протікають у ньому, а

характеризують лише його зовнішні властивості відносно сигналу. При

цьому зазвичай користуються заступними схемами, наведеними на рис. 1.3,

або їх модифікаціями.

а)

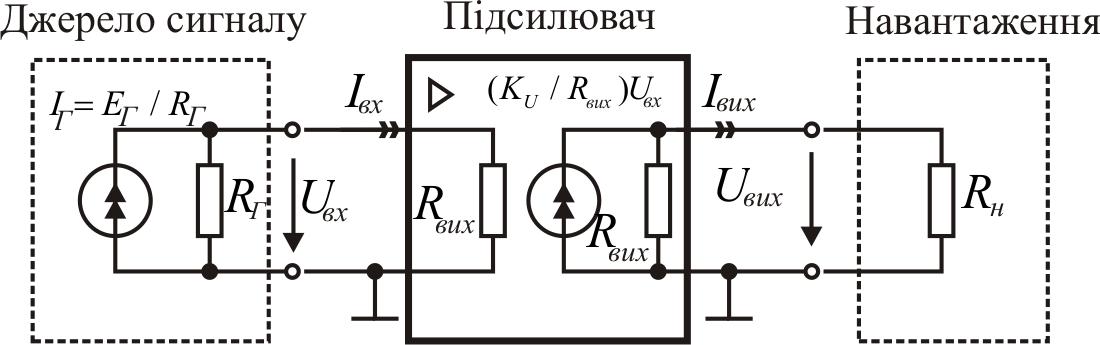
б)

Рис.1.3. Заступні схеми підсилювача за Тевеніном(а) і Нортоном(б)

Основні показники підсилювальних пристроїв наступні:

1)

Коефіцієнт підсилення визначається як відношення усталених

значень вихідної величини до вхідної на певній частоті f. Цими величинами

можуть бути напруги, струми або потужності. Тоді відповідно

використовують:

а) коефіцієнт підсилення за напругою K_U

 U вих^/U вх^;

б) коефіцієнт підсилення за струмом K_i Iвих^/Iвх^;

в) коефіцієнт підсилення за потужністю K_p Pвих^/Pвх^,

де U та I – амплітудні або ефективні значення напруг та струмів. У

загальному випадку коефіцієнт підсилення – комплексна величина:

  K exp( j ) ,

K

де K - модуль K , а   arctgK

 – аргумент K .

Часто користуються іншими відносними величинами, наприклад

децибелами( Á ):

K_U(Á )  20lg K_U, K_I(Á)  20lg K_I, K_P(Б ) 10lg K_P.

2)

Наскрізний коефіцієнт підсилення ( K_E) – характеризує ступінь

використання е.р.с, струму чи потужності джерела сигналу( EГ ). Зокрема,

наскрізний коефіцієнт підсилення за напругою(або коефіцієнт підсилення

е.р.с) це

3)

K_E U вих^/EГ

Вхідний опір( Rвх ) – це еквівалентний опір з боку входу

підсилювача, що є навантаженням для джерела вхідного сигналу.

R

вх

 U

/ I

вх вх

4)

Вихідний опір( Rвих ) – це еквівалентний опір з боку виходу

підсилювача. Слід зауважити, що в загальному випадку вхідний і вихідний

опори, як і коефіцієнти підсилення, можуть бути комплексними величинами.

Вони характеризують взаємодію підсилювача із зовнішніми колами.

5)

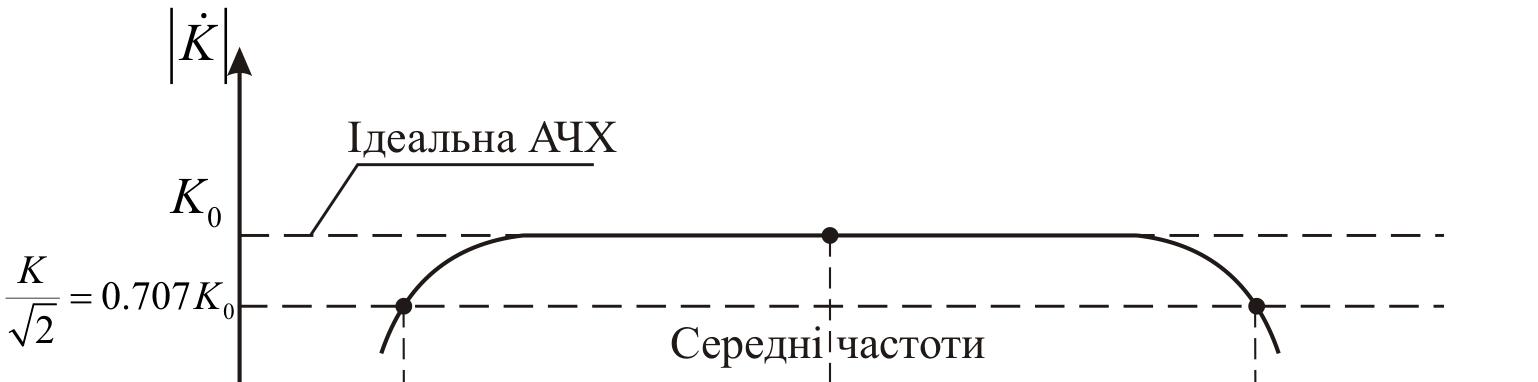
Амплітудно-частотною характеристикою(АЧХ) підсилювача

називається залежність модуля комплексного коефіцієнта підсилення K від

частоти f . Ідеальній АЧХ відповідає горизонтальна пряма K  K (рис.1.4).

Рис. 1.4. Амплітудно-частотна характеристика

0

Для оцінки частотних властивостей підсилювачів зручно користуватися

нормованим коефіцієнтом підсилення(Y)(або відносним підсиленням)

Y  K / K₀,

де K і K₀- коефіцієнти підсилення на довільній і середній частотах

відповідно. Залежність Y  Y f( ) також є відповідною частотною

характеристикою.

Величина, обернена відносному підсиленню, називається коефіцієнтом

частотних перекручень М.

 

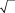
Діапазон 2

f

fв

 fн , в межах якого частотні перекручення не

перевищують заданих, називається смугою пропускання підсилювача.

Граничні частоти смуги пропускання, що відповідають зменшенню

коефіцієнта підсилення в 2 раз(на 3Б ), називають частотами нижнього

fн і верхнього fв зрізу. Це частоти, на яких потужність сигналу зменшується

у 2 рази(частоти половини потужності). Середня частота f₀ визначається як

f

 f f .

середнє геометричне число граничних частот. Тобто₀

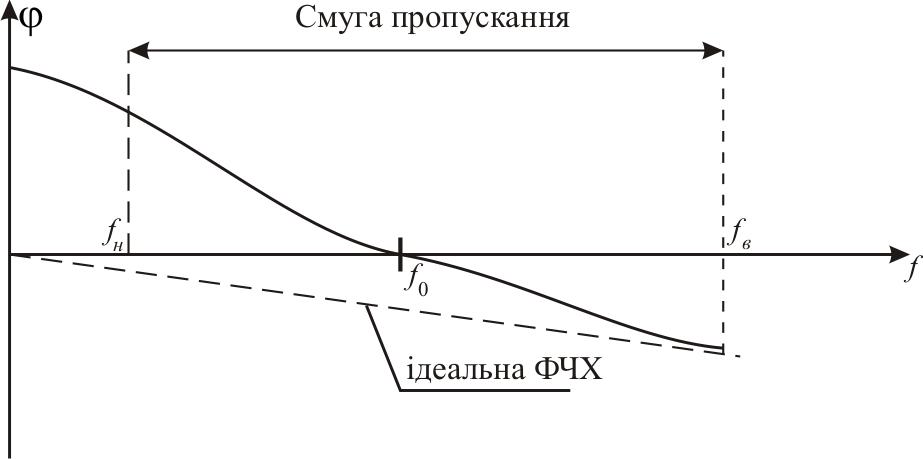
6) Фазочастотною характеристикою(ФЧХ)

н в

підсилювача

називається залежність аргументу комплексного коефіцієнта підсилення від

частоти(рис1.5).

Рис 1.5. Фазочастотна характеристика

На середній частоті

  k

,(k

 0 n) . Якщо ФЧХ ідеальна, то

  constf , тобто пряма. Відхилення від неї викликають фазові

перекручення.

Розглянуті частотні характеристики зручно будувати в прямокутних

координатах, де вісь частот має логарифмічний масштаб, інакше кажучи, у

напівлогарифмічних координатах.

7)

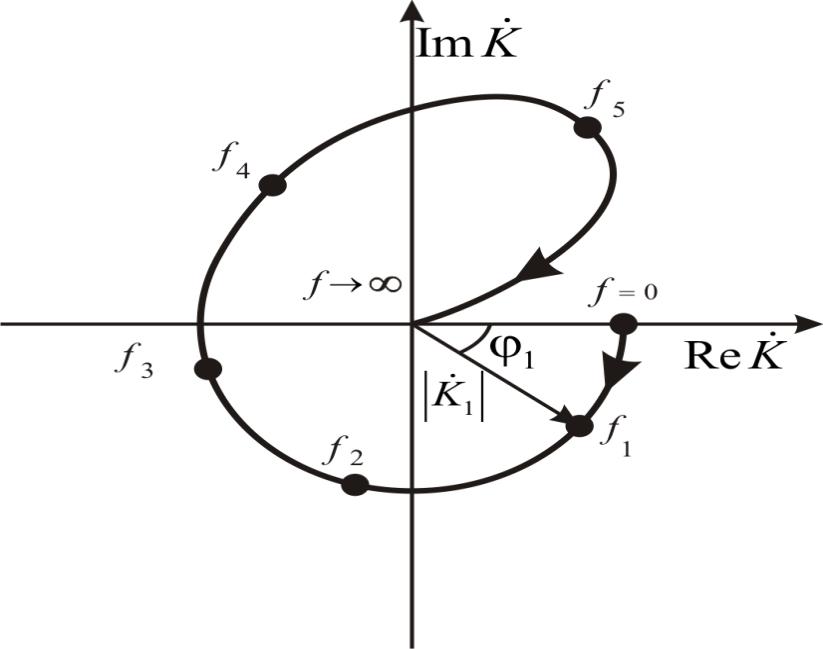
Частотна характеристика (ЧХ) (амплітудно-фазочастотна

характеристика(АФЧХ), векторна діаграма), об’єднує в одну залежність

амплітудно-частотну та фазочастотну характеристики підсилювача.

Здебільшого ЧХ будують на комплексній площині( Re , Im K ) в полярній

системі координат, де вона зображується кривою(частотний годограф), яку

описує кінець вектора K при зміні частоти вхідного сигналу від 0 до

∞(рис.1.6).

8)

Рис. 1.6. Амплітудно-фазочастотна характеристика

Логарифмічна АЧХ(ЛАЧХ) дає можливість операцію множення

ряду АЧХ замінити на більш просту операцію алгебраїчного сумування, що

може бути виконана і графічно. Для побудови ЛАЧХ ординату градуюють в

К( Á ), або користуються логарифмічними координатами. При цьому АЧХ

апроксимується відрізками прямих(графіки Боде), що значно спрощує

побудову та її аналіз.

9)

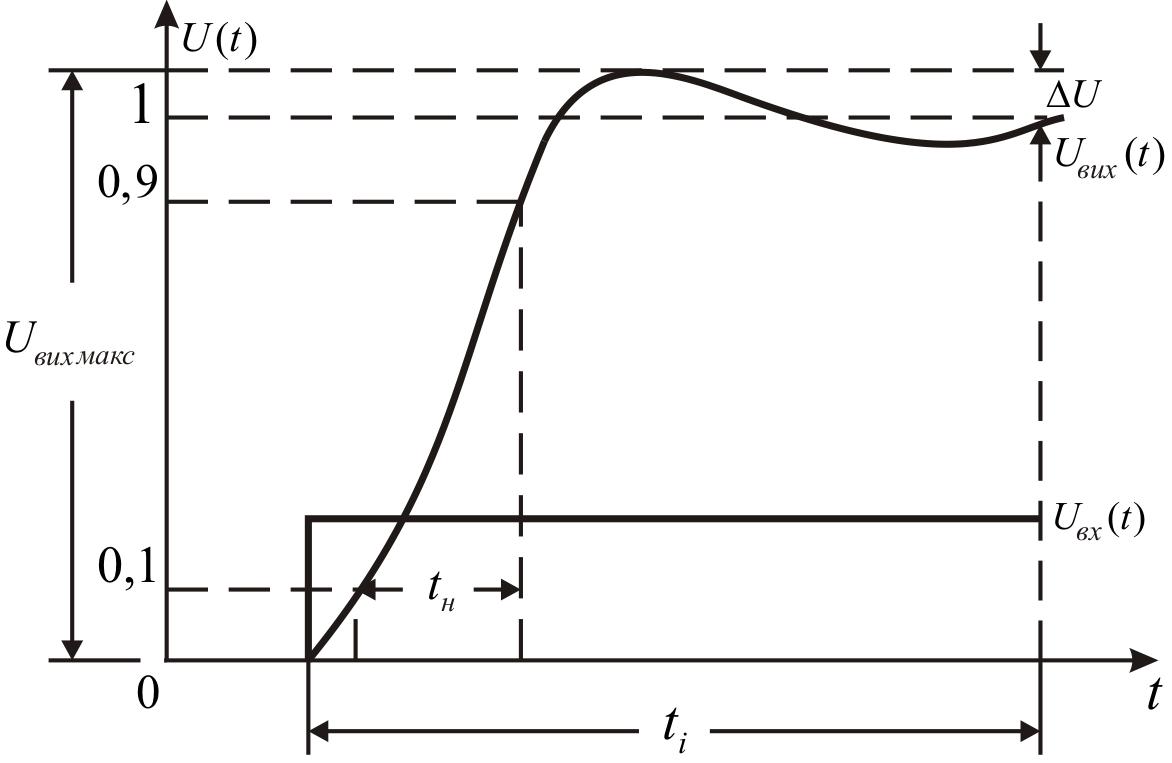
Перехідна характеристика(ПХ) підсилювача – на відміну від

попередніх – це часова характеристика. Вона є реакцією підсилювача на

стрибкоподібну зміну(стрибок Хевісайда) вхідної величини(рис.1.7).

Рис. 1.7. Перехідна характеристика

На рис. 1.7 використано наступні позначення: числа 0,1; 0,9; 1 –

відповідні рівні імпульсу вихідної напруги(U вих^); t_í – час наростання

імпульсу вихідної напруги, від рівня 0,1 до рівня 0,9; U – спад вершини

імпульсу вихідної напруги за час дії імпульсу( t_i).

ПХ важлива для імпульсних підсилювачів. Зауважимо, що між ЧХ і ПХ

у лінійному підсилювачі існує однозначний зв'язок. Оскільки

де  в – стала часу( в  1 / в ), то

2, 2 0,35

tн  2, 2 в^,



tн₂ fв



fв

.

Амплітудна характеристика(АХ) підсилювача описує залежність

амплітуди першої гармоніки вихідного сигналу від амплітуди гармонічного

вхідного сигналу певної частоти f₀(рис. 1.8). Ідеальна АХ має вигляд прямої,

що проходить через початок координат під кутом   arctgK₀.

Рис. 1.8. Амплітудна характеристика

Практично лінійна ділянка знизу обмежена напругами шумів(U1min^),

зверху – нелінійністю характеристик підсилювачів елементів(U1max^).

Відношення

U

1max

U

/ 1min

 D

Ï

називається динамічним діапазоном

підсилювача. Неперекручене підсилення можливе лише при умові, що

DП  Dсигналу^.

10) Режим підсилення малого сигналу, що гарантує лінійне

перетворення сигналів, реалізується при таких рівнях вхідного сигналу, коли

його подвоєння не викликає нелінійних перекручень, тобто амплітудна

характеристика має лінійний характер і досліджуваний параметр не змінює

своєї величини.

11) Логарифмічний масштаб. Побудова графіків і користування

ними ускладнюється, якщо величини вздовж осей змінюються у великих

межах. У цьому випадку користуються графіками Боде, тобто

логарифмічними координатами, що дає можливість не збільшувати розміри

рисунків. Для цього вздовж осей координатної сітки відкладають замість

значень функції та аргументу їх десяткові логарифми, а отриманим точкам

присвоюють назви відповідних величин(наприклад Б , Гц тощо).

Практично побудову координатної сітки логарифмічного масштабу

здійснюють так: одну або обидві координати розбивають на рівні

відрізки(декади), кожний з яких відповідає збільшенню відповідної змінної в

10 разів. Після цього кожний відрізок розбивають на дев’ять нерівних частин,

відкладаючи від лівого кінця відрізка 0.3, 0.47, 0.6, 0.7, 0.78, 0.85, 0.9, 0.95

його довжини. Одержаним точкам ділення присвоюють назву десятої долі

відрізка(0.1, 0.2, 0.3, 0.4, і т.д.) у відповідних одиницях(Гц тощо)(рис 1.9)

Рис. 1.9. Логарифмічні координати(графіки Боде)

Якщо по одній координаті прийнято логарифмічний масштаб, а по

іншій – звичайний(лінійний), то таку координатну сітку називають

напівлогарифмічною(рис. 1.10).

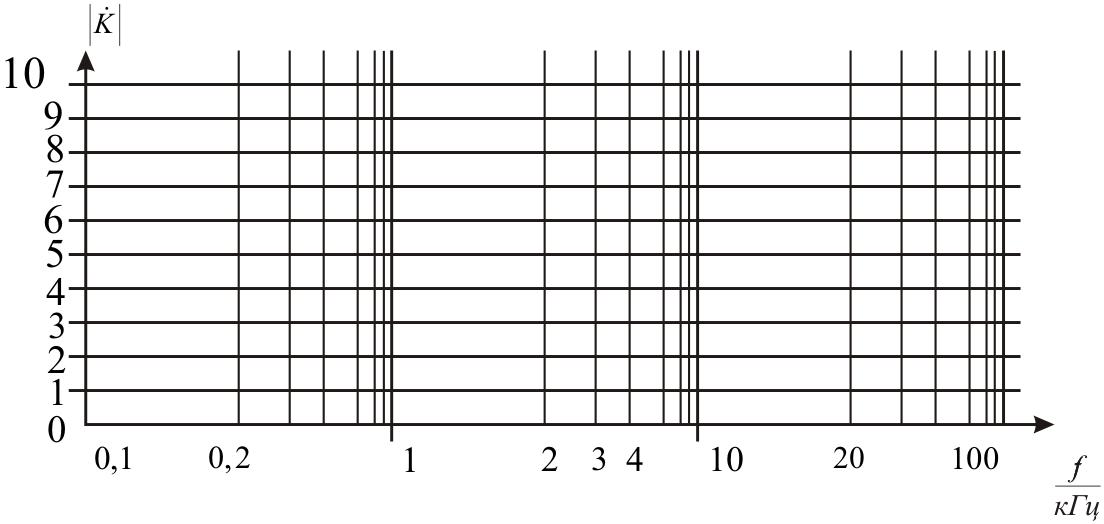
Рис. 1.10. Напівлогарифмічні координати

Крім десяткових логарифмів відношення( lg K ), що називаються

Белами(Б) або декадами, користуються ще іншими:

ln K

ln K  Nep(Непер), або rad(радіан); log₂K   octave(октава).

ln 2

Тобто, якщо збільшення в 10 разів – декада, в e раз – радіан, у 2 рази –

октава.

Причому:

1 rad = 1 Nep = 8,686 Á = 0,8686 decade = 1.442 octave,

якщо K (Б )  20lg K .

Але, якщо мова йде про відношення двох потужностей

K (Á)  10lg K_p, то логарифми відношень в усіх випадках множимо на 1/2

зберігаючи при цьому назви логарифмічних одиниць. Загалом тут

справедливими будуть співвідношення:

K_p e

K_p(непер)

[K_p(децибел)/20]

 10

 2

K_p(октава)

Тобто K_p(децибел) = 8,7 K_p(непер) = 6 K_p(октава).