МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Санкт-Петербургская

государственная академия аэрокосмического приборостроения

ИССЛЕДОВАНИЕ СТРУКТУРЫ

поля волн н₁₀ и н₂₀

ПРИ РАЗЛИЧНЫХ

НАГРУЗКАХ ВОЛНОВОДА

Методические указания к лабораторной работе

Санкт-Петербург 1996

Составители: Д.В. Благовещенский, Б.Т. Никитин

Рецензенты: кафедра радиотехнических систем; канд. техн. наук доц. В.К. Федотченко

В методических указаниях рассмотрена наглядная физическая мо­дель, демонстрирующая распространение электромагнитной волны в вол­новоде прямоугольного сечения_, и сопутствующие ей характеристики распространения.

Приводятся понятия волн Е и Н и определяются условия сущест­вования основного типа волны Н₁₀, а также волны Н₂₀.

Устанавливается физическое содержание режимов волн в волново­де и их связь с сопротивлением нагрузки и коэффициентами отражения, бегущей и стоячей волны.

Даются указания по подготовке к лабораторной работе, излага­ется методика выполнения экспериментальных исследований и порядок обработки полученных данных.

Методические указания предназначаются студентам, изучающим курс "Электродинамика -л распространение радиоволн" дневной, вечер­не": и заочной форм обучения.

Подготовлены к публикации кафедрой антенно-фидерных устройств и систем радиовидения по рекомендации методической комиссии радио­технического факультета Санкт-Петербургской государственной акаде­мии аэрскосмического приборостроения.

( С) Санкт-Петербургская государственная академия аэрокосмического приборостроения , 1996

Лицензии Лр №020341 от 27.12.91 г. Подписано в печать II. II. 96 г.

Формат 60х84 /16. Бумага тип.№3. Печать офсетная. Зак. №203 Усл.печ.л.2,4. Уч.-изд. л. 2,6.

Редакционно-издательский

Отдел оперативной полиграфии

СПбГААП

190000, Санкт-Петербург, ул.Б.Морская, 67

Цель работы:

ознакомление с принципами передачи электромагнитной энергии по направляющей системе из двух плоскостей: метод парциальных волн, волн типа Е и Н, продольное и поперечное волновые числа; изучение структуры электрического и магнитного полей внутри волновода для различных типов волн; параметры волновых процессов и их основные характеристики: длина волны в волноводе, критическая длина волны, фазовая скорость, волновое сопротивление; ознакомление с методикой представления волновода в виде эквивалентной длинной линии, с поня­тиями коэффициента отражения, коэффициентов бегущей и стоячей волн, входного сопротивления, а также с принципами возбуждения волн в волноводах; изучение особенностей СВЧ-измерений с помощью измерительной линии; экспериментальное исследование структуры полей волн типов Н₁₀ и Н₂₀ в прямоугольном металлическом волноводе.

I. СТРУКТУРА ПОЛЯ И ХАРАКТЕРИСТИКИ РАСПРОСТРАНЕНИЯ ВОЛНЫ В ВОЛНОВОДЕ

Под структурой поля понимается распределение составляющих электромагнитного поля в поперечном сечении и продольном направле­нии волновода.

Определение поперечных составляющих электромагнитного поля связано с решением уравнений Максвелла при учете граничных условий на металлических стенках волновода. Эта задача довольно сложна и трудоемка [1,2,3] . Более простое решение может быть получено ме­тодом парциальных волн. Достоинством этого метода является наглядность происходящих физических процессов в волноводе, а также он позволяет выявить физическое содержание каждой характеристики рас­пространения волн. Распределение составляющие поля в продольном направлении волновода зависит от характера нагрузки.

В данном разделе будут рассмотрены структура поля и характеристики распространения волны в волноводе бесконечной длины (что эквивалентно согласованной нагрузке) методом парциальных волн.

Пусть имеются две параллельные металлические пластины беско­нечной длины (рис.I.I). Одну пластину разместим в плоскости У0Z , а вторую - на удалении вдоль оси X. Направим под углом к оси ОХ плоскую волну. Часть этой волны попадет в пространство меж­ду пластинами и будет распространяться по оси 0Z за счет многократного отражения от пластин.

Выберем систему координат так, чтобы направление плоской вол­ны попадало в ее начало. Отраженная волна будет направлена под уг­лом на основании первого закона Снеллиуса [ I ] .

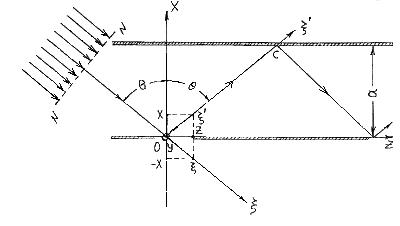
рис.I.I

Обозначим направление падающей волны как , а отраженной - и в соответствии с этим запишем падающую и отраженную волны в следующем виде:

; (I.I)

, (I.2)

где - фаза отраженной волны; К - волновое число.

Перемещение волны вдоль направлений и следует заме-

нить на соответствующие перемещения вдоль осей OX и OZ, так как

в этих координатах описывается волновой процесс между пластинами.

Из рис.I.I определяем

(I.3)

. (I.4)

Между пластинами происходит непрерывное пересечение падающих (двигающихся от верхней пластины) и отраженных (идущих от нижней пластины) волн. На отрезке ОС (см.рис.I.I) любые точки являются точками пересечения с падающими волнами. Рассмотрим одну из них с координатами Х,Z (рис.I.2).

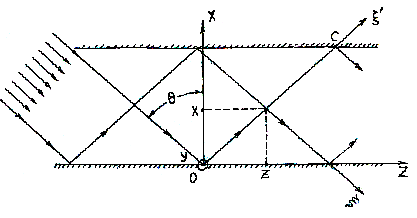
Рис.1.2

В этой точке складываются две волны - падающая и отраженная. В соответствии с рис. I.2 падающая волна дважды отражалась от плас­тины, а отраженная - только один раз. Поэтому полная фаза при отражении от пластин у падающей волны будет равна , а у отраженной - . В общем случае при достаточном уда­лении Z от начала координат

, (I.5)

где n = 1,2,3, ...

С учетом формул (I.3), (I.4) и (I.5) выражение для полного по­ля будет иметь следующий вид:

В показателях степени множители при переменных X и Z имеют смысл волнового числа. Множитель при X есть поперечное волновое число

(I.6) а при Z - продольное волновое число, которое еще называют фазовой постоянной

(I.7)

С учётом введённых обозначений полное поле

. (I.8)

Окончательное выражение для полного поля может быть получено при определении значения фазы волны, отраженной от металлической пластины.

Вектор электрического поля Е всегда ориентирован перпендику­лярно относительно направления движения волны. В общем случае Е может быть произвольно ориентирован, но его всегда можно разложить по ортогональным осям. Вследствие этого определение фазы отражения распадается на две задачи. В одной задаче ориентируем вектор Е па­раллельно пластинам, т.е. в плоскости У0Z (рис. 1.3, а), а в другой - в плоскости Х0Z , перпендикулярно направлению движения (рис. 1.3, б). При этом, в отличие от общего случая, в данных задачах векторы Е и Н обозначены как Е’ и Н’.

Из рис. 1.3,а, видно, что распространяющаяся между пластинами волна состоит из поперечных электрического поля и магнитного поля E’_y, Н’_х , а также продольного магнитного поля Н’_z . Волну этого ви­да принято называть типа Н.

Иногда, но очень редко, волну типа Н называют ТЕ, что соответствует

поперечно-электрической волне. На рис.I.3,6 полный набор составляющих , имеет электрическое поле и поэтому эту волну называют типа Е или ТМ (поперечно-магнитная волна).

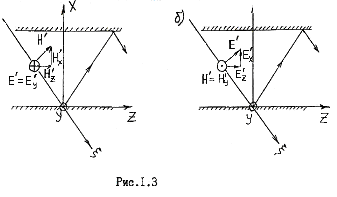
Для определения фазы отраженной волны следует воспользоваться граничными условиями [ I ] . Будем считать, что металлическая пластина имеет проводимость  = ∞, а значит падающая волна полностью отражается. У волны типа Н вектор электрического поля пара­ллелен границе раздела, которой является металлическая пластина. Непосредственно на границе (X = 0) полное электрическое поле равно нулю

(I.9)

Анализируя выражение (I.8), устанавливаем, что для выполнения

условия (I.9) достаточно, чтобы . Это равенство будет выполняться при .

Преобразуем выражение (I.8) с учетом полученной фазы отражен­ной волны

.

В дальнейших выкладках для упрощения записи последней формулы можно считать n четным. Чтобы определить поперечное волновое число, следует использовать граничные условия для второй металлической

пластины, когда x = a:

где . Это равенство будет выполняться только тогда, когда аргумент при синусе будет равен

где = 1,2,3 …

Отсюда

. (1.10)

В окончательном виде полное поле с учетом равенства (1.10) и сделанных предложений примет следующий вид:

(1.11)

Как видно из формулы (1.11), между пластинами устанавливается стоячая волна, у которой максимальная амплитуда в пучности равна . Число показывает, какое число полуволн укладывается между пластинами на отрезке " a " (рис.1.4).

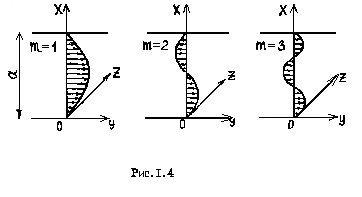
Следует особо отметить, что если увеличить или уменьшить расстояние между пластинами, то характер изменения поперечной составляющей

электрического поля останется таким же, как представлено на рис . 1 . 4 .

Определим условие, при котором волновой процесс между пласти­нами с заданным расстоянием между ними будет невозможен.

Возьмем выражение (1.10) и заменим в соответствии с (1.6)

;

; (1.12)

Если =0,то согласно рис.1.1 перемещения волны вдоль оси Z не будет. В этом случае равенство (1.12) будет выполняться. Посколь­ку величина задана, то выполнение этого равенства будет возможным за счет выбора длины волны, которую принято называть критической:

. (1.13)

Для того, чтобы волновой процесс между пластинами существовал, необходимо, чтобы рабочая длина волны была меньше . Чтобы доказать этот факт, используем равенство (1.12), которое запишем в следующем виде:

С учётом (1.13) далее имеем

.

Если исключить =0, то <1 и, следовательно, < .

Для дополнительного доказательства о прекращении волнового процесса между пластинами при =0 обратимся к продольному волновому числу . Преобразуем выражение (1.7) следующим обра­зом:

При =0( = ) величина =0, а .

Следовательно, множитель, характеризующий волновой процесс в жении (1.11),будет отсутствовать. Следует напомнить, что при описании волнового процесса необходимо учитывать время t [ I ] .

Тогда выражение (1.11) с учетом того, что =0, будет вы­глядеть следующим образом:

(1.15)

Э та формула описывает колебательный процесс. При зна­чение

, а

г де --------- коэффициент затухания.

Здесь с точки зрения физики явления в выражении для берется только знак минус. В этом случае колебательный процесс происходит с затуханием. По мере увеличения Z будет уменьшаться амплитуда поля. Установим условие существования волн между пласти­нами с различными индексами m при . Для этого используем формулу (1.13). При m=1 значение . Сле­довательно, для существования этой волны необходимо, чтобы .

Для m = 2 и и т.д. На рис. 1.5 сделаны соответствующие построения.

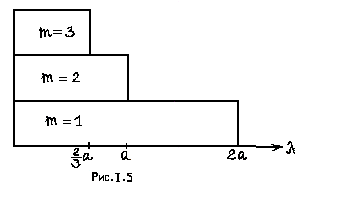
Из рис.1.5 видно, что если близка к нулю, то между пла­стинами могут одновременно существовать множество волн с различными индексами m. Но если установить для длины волны пределы

, то будет существовать только единственная волна с индексом m =1. Ее принято называть основной. Исходя из физического , волновое число К определяет величину набега фазы при прохождении волной единицы пути

. (1.14)

При этом волна распространяется в свободном неограниченном пространстве и соответствующая ей длина волны также относится к свободному пространству

, (1.15)

где - фазовая скорость волны в свободном пространстве; - период колебания; - абсолютные магнитная и диэлектрическая проницаемости среды (свободного прост­ранства).

Продольное волновое число имеет то же содержание, что и К, но только оно учитывает, что волна распространяется между пластинами

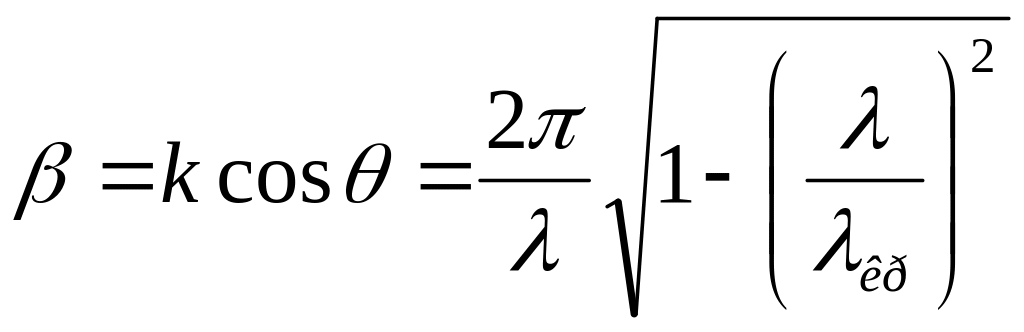
(1.16)

Сравнивая выражение (1.16) с (1.14), устанавливаем, что между пластинами длина волны

(1.17)

Для того чтобы путь, проходимый волной между пластинами за один период, был бы равен , (см.формулу (1.15)), фазовая ско­рость должна быть следующей:

(1.18)

Непосредственно из формул (1.17), (1.18) следует, что для длины волны и фазовой скорости всегда выполняются следующие нера­венства:

.

Формулы (1.17), (1.18) можно получить, исходя из простых физических соображений. На произвольном направлении отраженной от верхней пластины волны возьмем две точки C, d (рис.1.6).

Пунктирными линиями здесь обозначены соответствующие точкам С и d фронты отраженной волны. Если вдоль направления отражен­ной волны расстояние между фронтами равно Сd, то вдоль оси 0Z

.

Примем . Тогда будет являться длиной волны между пластинами

Скорость перемещения фазы (фазовая скорость) волны между пластинами

Ч тобы определить распределение магнитного поля между пластинами , необходимо использовать граничные условия. Для этого предваритель­но необходимо вектор магнитного поля разложить по ортогональным осям (см. рис. 1.3, а) . Составляющая нормально ориентирована отно­сительно металлических пластин. Согласно граничным условиям при отражении фаза изменится на величину [1] Ис­пользуя выше приведенную методику, получим

, (1.19)

где - максимальная амплитуда в пучности стоячей вол­ны. Сравнивая выражение (1.19) с (1.11), убеждаемся в ток, что и синфазны и закон распределения амплитуд у них одинаков.

Выразил амплитуду в пучности Н_ППХ через амплитуду в пучности электрического поля Е_пп. В плоской волне амплитуды электрическо­го и магнитного полей однозначно связаны между собой через волновое (или характеристическое) сопротивление свободного пространства [1]

Из рис. 1.3,а видно, что

.

Подставим выражения (1.20) и (1.21) в (1.19). После преобразований получим

, (1.22)

где - волновое сопротивление простран­ства между пластинами.

Продольная составляющая - при отражении волны от металлических

пластин фазу не меняет ( = 0). Используя выше изложенную методику, получим

, (1.23)

где ;

(1.24)

Подставив выражения (1.20) и (1.24) в (1.23),: нуго составляющую магнитного поля в следующем виде:

. (1.25)

Как видно, продольная составляющая магнитного поля отличается от поперечных составляющих не только законами распределения амплитуд, но и фазой. Поперечные составляющие имеют начальную фазу , а у продольной начальная фаза равна нулю.

Различие в фазах имеет особый смысл и связан он с переносом энергии электромагнитного поля между пластинами.

Активная плотность мощности определяется следующей формулой [4]:

(1.26)

Подставим в нее выражения для электрического поля (1.11) и составляющих магнитных полей (1.22) и (1.25)

Полная плотность мощности состоит из двух слагаемых. Одно из них не равно нулю и характеризуется вектором, который направлен вдоль оси 0Z:

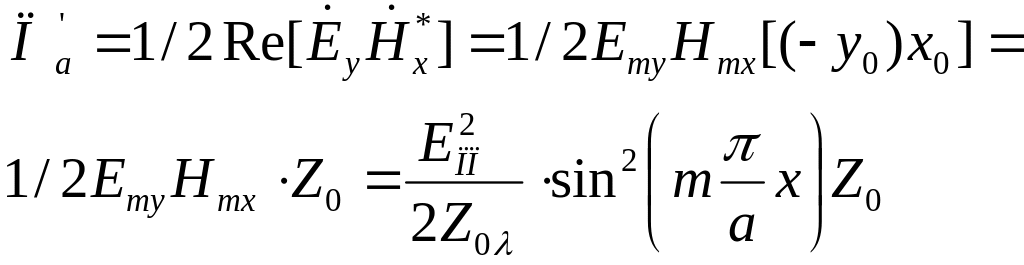
где Х₀, У₀,Z₀ - орты прямоугольной системы координат; - амплитуды. Второе слагаемое плотности мощности равно нулю:

поскольку

В переносе энергии вдоль пластин (по оси 0Z ) участвуют толь­ко поперечные составляющие магнитного поля.

Наглядное представление о рассматриваемых процессах можно по­лучить с помощью рис 1.7, на котором вектор плотности мощности ,от­раженной от верхней пластины волны, разложен на две ортогональные составляющие.

Рис.1.7

Как видно из рис 1.7, вектор плотности мощности П’’ направлен вдоль оси ОХ. В этом случае происходит взаимный обмен энергиями между магнитным и электрическими полями, что эквивалентно процессам, связанным с реактивной энергией.

Рассмотрим, какие изменения в структуре поля и в характеристиках

распространения волны произойдут, если дополнительно ограничить пространство между пластинами по вертикали. Для этого к исходным пластинам добавим вторую пару параллельных пластин таким образом, чтобы они все вместе образовали полую металлическую трубу прямоу­гольного сечения размером a x b (рис.1.8). Данная конструкция получила название волновод.

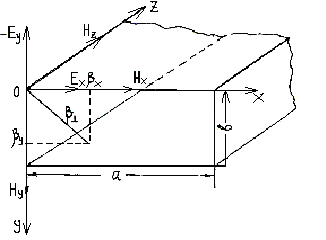
Рис.1.8

Между расположенными параллельно плоскости Х0Z пластинами на удалении b друг от друга волна распространяется за счет многократно-

го отражения с участием составляющих поля В волноводе происходит одновременно отражение от обеих пар металлических плас­тин, следовательно, в формировании структуры поля волны Н участвуют следующие составляющие:

Если поперечное волновое число, ориентированное вдоль оси ОХ, равно , то поперечное число, ориентированное вдоль оси ОУ, определяется аналогичным образом

Полное поперечное число будет равно (см.рис.1.8)

(1.27)

где m=0,1,2, …, n=0,1,2, …, при этом одновременно m и n не могут быть равны нулю.

С другой стороны, (см.(1.6)).

При =0 волновой процесс прекращается и можно определить критическую длину волны

, откуда

. (1.28)

остальные характеристики будут следующими:

(1.29)

(1.30)

(1.31)

где

Как видно из рис.1.8, каждая поперечная составляющая электромагнитного поля относительно одной пары стенок ориентирована тангенциально, а относительно другой пары - нормально. У тангенциаль­ных электрических полей фаза отражения равна , а у нормальных - нулю. У магнитных полей наоборот. Тангенциальные составляющие име­ют фазу отражения нуль, а нормальные - [ I] . Используя выше­рассмотренную методику с учетом граничных условий, получим составляющие волны Н в следующем виде:

(1.32)

(1.33)

(1.34)

(1.35)

(1.36)

При обозначении магнитной волны вводятся индексы . Индекс указывает, какое число полуволн укладывается вдоль широкой стенки, а индекс - вдоль узкой стенки волновода. Если , или равны нулю, то вдоль широкой или узкой стенок волновода поле не изменяется. В волноводе прямоугольного сечения широкую стенку обозначают , а узкую - . Основной волне соответствует наибольшая критическая длина волны. Анализируя выражение (1.28) и учитывая, что и то, что одно из чисел или может равняться нулю, устанавливаем, что наибольшая критическая волна будет при =1 и =0

Это значение совпадает с ранее полученным (1.13). В соот­ветствии с рис.1.5 для реализации =1 необходимо выполнить следующее неравенство:

(1.37)

При = 0 составляющие поля не должны изменяться вдоль уз­кой стенки. Чтобы этого не произошло,

(1.38)

Основную магнитную волну записывают как .

Используя выше приведенную методику, можно для электрической волны (см.рис.1.3,б) определить составляющие поля и характе­ристики распространения. Критическая длина волны определяется по формуле (1.28). Волна типа Е может существовать в волноводе толь­ко тогда, когда индексы и не равны нулю. Следовательно, максимальная критическая длина волны типа будет меньше, чем у волны :

А так как это условие выполняется всегда, то при в волноводе будет присутствовать только единственная волна . Для построения структуры поля волны в поперечном сечении вол­новода положим Z=0- Тогда из выражений (1.32), (1.34), (1.36) получим распределения амплитуд полей в следующем виде:

(1.39)

Для наглядности распределение каждой составляющей изображено на рис.1.9.

Чтобы построить структуру поля в продольном направлении вол­новода, следует перейти от комплексной формы составляющих к реаль­ной форме, которая является реальной частью комплексного числа:

(1.40)

(1.41)

(1.42)

Искомую структуру полей внутри волновода изобразим в плоскости Х0Z (рис.1.1О).

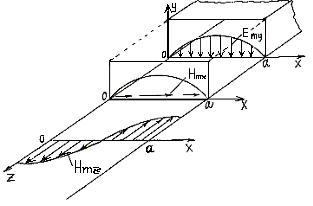
Рис.1.9

Непосредственно в этой плоскости будут располагаться вектора маг­нитных составляющих. Вектор электрического поля будет нормален к плоскости Х0Z .

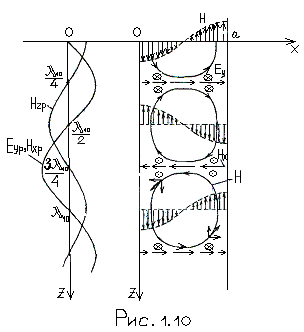
Определим положения поперечных сечений, где присутствует только

одна из составляющих магнитного поля. Как видно из рис.1.10, эти сечения чередуются через . Между этими сечениями будут присутствовать обе ортогональные составляющие магнитного поля, их геометрическая сумма укажет на величину и на направление вектора полного магнитного поля. В области между сечениями и (X найдутся такие точки, где вектора магнитного поля будут одинаковыми по абсолютной величине, но различным образом ориентированы. Совокупность всех таких точек образует замкнутую кривую, которую принято называть магнитной линией. В соседней области, отстоящей от первой на получим

сходную магнитную линию, но только ее направление будет обрат­ным.

Структура поля (поперечная и продольная) волны может быть образована из простейшей ячейки, соответствующей волне (см.рис.1.10), На рис. 1.11 представлены структуры волн

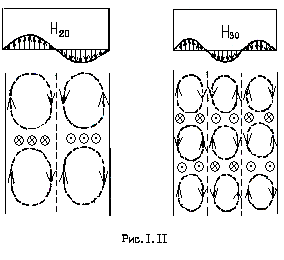
Представленные изображения структур поля на рис.1.10, 1.11, соответствуют фиксированному значению времени t = 0. В действительности эти структуры перемещаются в направлении положительной оси ОZ со скоростью (см.формулу 1.16).

В заключение следует еще раз подчеркнуть, что данные структу­ры были построены в предположении бесконечной длины волновода, что соответствует режиму бегущей волны.