2.3 Применение теорем Менелая и Чевы в решении стереометрических задач.

Стереометрия – это геометрия в пространстве. В основном задачи по стереометрии сводятся к геометрическим задачам на плоскости, поскольку обычно требуемые элементы можно найти, сведя исходную задачу к нескольким планиметрическим.

Задачи эти довольно-таки трудны, здесь главное опыт. А знание теоремы Менелая – это просто находка для решения стереометрических задач.

Она может оказаться очень полезной при изучении темы «Объемы тел» в курсе геометрии 11 класса.

Ниже приведем несколько задач, предлагавшихся на вступительных экзаменах в вузы.

Владение методами их решения дает большое преимущество перед школьниками, которые не умеют решать такого рода задачи.

Задача 1. На продолжении ребра АС правильной треугольной пирамиды ABCD с вершиной D взята точка K так, что КА:КС=3:4, а на ребре DC взята точка L так, что DL:LC=2:1. В каком отношении делит объем пирамиды плоскость, проходящая через точки B, L и К?

Дано:DABC – правильная пирамида, , , , , BLK –

плоскость, - объем верхней части пирамиды, - объем нижней части пирамиды.

Найти: .

Р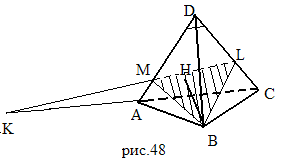 ешение:

1) Построим сечение пирамиды DABC плоскостью BLK.

соединяем, соединяем,

, соединяем, MLB - искомое сечение (рис.48).

2) Найдем , где - объем всей пирамиды.

Пусть BH – высота пирамиды DABC, проведенная из вершины В, но она – высота и BMDL.

; V= , V = ;

;

, - ?

3) Из ADC: , , , .

По теореме Менелая , .

, , .

(или: во всем объеме пирамиды 33 части, в верхней – 16, значит, 33-16=17 – частей

составляет . Тогда ) Ответ: .

Задача 2. Дана правильная четырехугольная пирамида с вершиной . На продолжении ребра взята точка так, что . Через точки М, В и середину ребра проведена плоскость. В каком отношении она делит объем пирамиды?

Решение:

1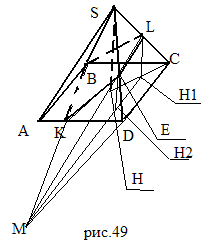 ) Построим сечение плоскостью . (по условию).

а) , соединяем BL;

б) , соединяем LM;

в) , соединяем BM , ; , соединяем

г) четырехугольник BLEK – искомое сечение.

2) Обозначим объемы нижней части пирамиды, верхней части и всей пирамиды , и соответственно, сторону основания – .

( MBC - прямоугольный)

; MKD~ MBC по двум углам ;

3) ~ по двум углам .

4) Рассмотрим MLC и секущую . .

По теореме Менелая ;

Значит ; .

5) .

6) SCH~ по двум углам .

Пусть , тогда , .

.

7)

, т.е. V содержит 60 частей, на приходится 31 часть.

Ответ: 29:31

Задача 3. Дана правильная треугольная призма с боковыми ребрами , и . Причем на продолжении ребра взята точка так, что . Через точки , и середину ребра проведена плоскость. В каком отношении она делит объем призмы?

Р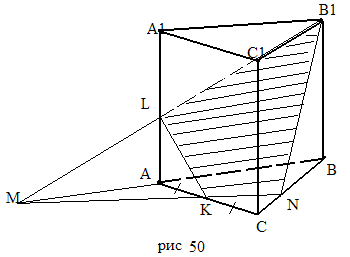 ешение:

1) Построение сечения:

а) , соединяем MB , .

б) , соединяем , .

в) , соединяем .

г) четырехугольник - искомое сечение.

2) Пусть , , - объемы нижней части, верхней части и всей призмы, - высота призмы, - сторона основания.

;

MLA~ ;

Рассмотрим ABC, - секущая, .

По теореме Менелая .

, , ; , , , .

,

- части приходится на . .

Ответ: 13:23

Задачи для самостоятельного решения:

1. Дана правильная четырехугольная пирамида с вершиной . На продолжении ребра взята точка так, что . Через точку и середины ребер и проведена плоскость. В каком отношении она делит объем пирамиды?

2. Высота правильной призмы равна стороне ее основания. Точки и - середины ребер и соответственно. Найти площадь сечения призмы плоскостью, проходящей через точки , и , если сторона основания равна .

3. В тетраэдре ZABC проведено сечение плоскостью. Точки M,N,P,Q принадлежат плоскости и ребрам ZA,AB,BC,CZ соответственно, причем ZM= MA, AN= NB, BP= PC, CQ= QZ. В каком отношении эта плоскость делит объем пирамиды?

4. Объем тетраэдра ZABC равен 7. Через середины ребер ZA и CB проведена плоскость, пересекающая ребро ZC в точке Q, а ребро AB – в точке L. При этом

ZQ:QC=2:5, AL:LB=2:5. Найдите площадь сечения тетраэдра указанной плоскостью, если расстояние до нее от вершины A равно 1.

Использовать приведенные задачи можно и на уроках заключительного повторения в 11 классе, причем здесь необходима целенаправленная работа по систематизации и углублению знаний учащихся. В работе можно использовать задания, приведенные в п.2.1, в приложении 2. Особое внимание нужно уделить планиметрическим задачам, так как они составляют основную массу задач вступительных экзаменов в вузы. Наличие заданий различной трудности позволит вести дифференцированную работу с учащимися.

Заключение

Крылатую фразу Козьмы Пруткова «Никто не обнимет необъятного» в полной мере можно отнести и к геометрии треугольника. В самом деле, треугольник, как кладезь прекрасных и поразительных геометрических конструкций, поистине неисчерпаем. Их пестрота и изобилие, с трудом поддающиеся какой – либо систематизации, не могут не восхищать[10, с.3].

Многие удивительные соотношения и изящные геометрические факты вошли

в основной курс планиметрии, некоторые замечательные теоремы включены в программу профильных классов.

Данная работа посвящена двум таким теоремам – теореме Менелая и теореме Чевы, которые позволяют решать многие, казалось бы, сложные математические задачи просто, красиво и понятно. Кроме того, здесь поднимается огромный пласт основных фактов и понятий школьного курса планиметрии: подобие треугольников; свойства и признаки параллельных прямых; метрические соотношения в треугольнике; окружность, описанная около треугольника и вписанная в него. Предложенный материал дает учащимся возможность познакомиться с интересными, нестандартными вопросами геометрии, с еще одним методом решения геометрических задач.

Рассматриваемые в работе вопросы выходят за рамки обязательного содержания. Вместе с тем, они тесно примыкают к основному курсу. Поэтому их изучение способствует совершенствованию и развитию важнейших математических знаний и умений, предусмотренных школьной программой, помогает оценить свои возможности по математике и более осознанно выбрать профиль дальнейшего обучения (9 класс), подготовиться к вступительным экзаменам (11 класс).

Предлагаемые в работе задачи интересны и часто не просты в решении, что позволяет повысить учебную мотивацию школьников. Эти задачи рассчитаны в первую очередь на учащихся, интересующихся математикой, желающих иметь хорошие навыки в решении геометрических задач. Вместе с тем, их содержание позволяет ученику любого уровня активно включиться в учебно - познавательный процесс и максимально проявить себя: занятия могут проводиться на высоком уровне сложности, но включать вопросы, доступные и интересные всем учащимся.

Думается, что представленный в работе материал будет полезен коллегам и может стать основой соответствующего теме элективного курса по выбору в системе предпрофильной подготовки по математике.

Литература.

1. Авдонин Н.И., Авдонина Е.П., Зорин В.А., Казимирова В.М.,

Новоженов М.М. Математика - 2000: Предварительное тестирование.-

Нижний Новгород, ННГУ, 2000- 237с.

2. Авдонин Н.И., Авдонина Е.П., Алексеев А.А., Калинин А.В.,

Новоженов М.М. Математика: Предварительное тестирование. – Нижний

Новгород: ННГУ, 2005.- 132с.

3. Алексеев В. Бородин П. и др. Планиметрия. Материалы вступительных

экзаменов в МГУ / Математика. Еженедельное приложение к газете « Первое

сентября», 2000,-№8.-с.18-22

4. Атанасян Л.С., Бутузов В.Ф., Кадомцев С. Б., Шестаков С.А., Юдина И.И.

Геометрия. Доп. главы к учебнику 8 кл.: Учеб. пособие для учащихся школ и

классов с углубл. изуч. математики / Л.С. Атанасян, В.Ф. Бутузов,

С.Б.Кадомцев и др.-М.: Вита-пресс, 2004. - 208 с.

5. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

Геометрия: Учебник для 7-9 классов средней школы / Л.С. Атанасян,

В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1990. – 336с.

6. Иванов К.А. О пропорциональных отрезках в треугольнике / Математика в

школе, 2004. - №8. – с.20-25

7. Иванова Т.А., Перевощикова Е.Н., Григорьева Т.П., Кузнецова Л.И.

Теоретические основы обучения математике в средней школе: Учебное

пособие/Т.А Иванова, Е.Н. Перевощикова, Т.П. Григорьева, Л.И.Кузнецова;

под ред. проф. Т.А.Ивановой. – Н.Новгород: НГПУ, 2003. - 320с.

8. Качалкина Е.Применение теорем Чевы и Менелая/Математика. Издательский

дом «Первое сентября», 2004, - №13. – с.23-26

9. Качалкина Е. Применение теорем Чевы и Менелая / Математика.

Издательский дом «Первое сентября», 2004,- №14. – с.24-27

10.Мякишев А.Г. Элементы геометрии треугольника. – Библиотека

«Математическое просвещение» - М.: Издательство Московского центра

непрерывного математического образования, 2002. – 32с.

11.Олимпиада Таланты Земли Нижегородской – Математика –

http://www.unn.ru/olimp/olimp/archiv/tzn 2004

12. Пантелеев В.П. Пропорциональные отрезки и то, что за ними/ Математика в

школе, 2004,- №8. – с.25-31

13.Портал естественных наук. Дополнительные соотношения между

элементами в треугольнике. – http://e-science.ru/math/theory

14. Прасолов В.В. Задачи по планиметрии. Часть 1.- М.: Наука. Гл. ред. физ. –

мат. лит., 1991. – 320с.

15. Саранцев Г.И. Упражнения в обучении математике. – М.: Просвещение,

2005. – 254с.

16. Стандарт среднего (полного) общего образования по математике /

Математика в школе, 2004, - №4. – с.12-16

17. Тихов М.С., Алексеев А.А., Макеев Н.Г. Математика: 2006.

Предварительное тестирование. – Н.Новгород: ННГУ, 2006. – 67с.

18. Тихов М.С., Алексеев А.А. Математика:2006. Летнее тестирование. –

Нижний Новгород: Издательство Нижегородского университета, 2006. – 72с.

19. Ткачук В.В. Математика – абитуриенту. – М: МЦНМО, 2005. – 944с.

20. Фарков А.В. Учимся решать олимпиадные задачи. Геометрия. 5-11 классы/

А.В. Фарков. – М: Айрис-пресс, 2006. – 128с.

21. Черкасов О.Ю., Якушев А.Г. Математика: Интенсивный курс подготовки к

экзамену. – М: Айрис-пресс ,Рольф, 2001. – 416с.

22. Шарыгин И.Ф. Геометрия 7-9 кл.: Учеб. для общеобразоват. учеб.завед.- М:

Дрофа, 2000. – 368с.

23. Шарыгин И.Ф. Планиметрия, 9-11 кл.: От учебной задачи к творческой:

Пособие для учащихся. – М: Дрофа, 2001. – 400с.

24. Шестаков С.А. Сборник задач для подготовки и проведения письменного

экзамена по алгебре за курс основной школы: 9-й кл. / С.А.Шестаков,

И.Р.Высоцкий, Л.И.Звавич; под ред. С.А.Шестакова.–М: АСТ:Астрель,2006.–

255с.

Приложение 1.

Разные задачи.

Попробуйте решить эти задачи с помощью теоремы Менелая.

1. Диагонали выпуклого четырехугольника ABCD пересекаются в точке Q. Через

точку Q проведена прямая, пересекающая стороны AB и CD в точках K и L

соответственно. Найти отношение DL:LC, если известно, что AK=KB,

BQ:QD=2:3, CQ:QA=3:4.

2.Диагонали выпуклого четырехугольника KLMN пересекаются в точке Q. Через

точку Q проведена прямая, пересекающая стороны KL и MN в точках A и B

соответственно. Найти отношение MQ:QN, если известно, что KA:BM=5:6,

LQ:QK=3:2, NB:AL=4:1.[2, с.61] (в указанной литературе приводится другой

способ решения).

3. Биссектриса угла A треугольника ABC делит медиану, проведенную из

вершины B, в отношении 5:4, считая от вершины B. В каком отношении,

считая от вершины C, эта биссектриса делит медиану, проведенную из

вершины C?

4. На стороне AC треугольника ABC выбрана точка B , а на стороне AB – точка

C так, что В каком отношении, считая от вершин

треугольника, точка пересечения отрезков BB и CC делит каждый из этих

отрезков?[24, с.189]

5. В тетраэдре ABCD через середины K и N ребер AD и BC проведена плоскость,

пересекающая ребра AB и CD соответственно в точках M и L. Площадь

четырехугольника KLMN равна 16, а . Вычислите

расстояние от вершины A до плоскости KLNM, если объем многогранника

NACLK равен 40.

6. В тетраэдре KLMN проведено сечение плоскостью. Точки A,B,C,D

принадлежат плоскости и ребрам KN,LN,LM и KM соответственно, причем

и . Найти

отношение объемов частей, на которые плоскость ABCD делит тетраэдр.

7. В пирамиде ABCD проведено сечение KMLN так, что точка K лежит на ребре

AD, точка M – на ребре DC, точка N – на ребре AB, точка L - -на ребре BC, и O-

точка пересечения диагоналей KL и MN четырехугольника KMLN. Сечение

KMLN делит пирамиду на две части. Найти отношение объемов этих частей,

если известны следующие соотношения между длинами отрезков:

[19, с.464]

50