
Цель работы: изучение устройства, назначения и принципа действия рычажных лабораторных весов, практическое освоение методики измерения массы различными методами взвешивания.

Теоретическая часть
Масса характеризует собой количество материи и является мерой инерционных и гравитационных свойств тела и для каждого тела является неизменной. Сила тяжести тела, его вес, есть гравитационная сила, то есть сила, вызванная гравитационным притяжением тела к Земле. Таким образом, весом называется сила, с которой оно давит на опору под действием притяжения Земли. Масса и сила тяжести связаны между собой определенной зависимостью.
Сила тяжести выражается формулой:
![]()
где М - масса земли; m - масса тела; R - расстояние от центра тяжести тела до центра Земли; g - гравитационная постоянная.
Сила тяжести одного и того же тела в зависимости от места его расположения на земной поверхности в силу того, что фигура Земли по форме наиболее близка к эллипсоиду вращения, будет разной.
Одинаковые массы при сличении их взвешиванием на весах будут обладать одинаковой силой тяжести только при соблюдении следующих условий:
а) сличаемые массы одинаково расположены по отношению к Земле;
б) сличаемые тела помещены в безвоздушное пространство.
Первое условие вполне выполнимо, а для устранения влияния среды, то есть соблюдения второго условия (учитывая, что никакие точные взвешивания в пустоте не производят в действительности), при точных взвешиваниях в результат взвешивания вводят поправку, зависящую от объемов сличаемых масс и плотности среды.
Устройство, назначение и измерения с помощью весов
Весы – прибор для измерения массы, чувствительный элемент которого воспринимает вес груза и преобразует его в величину, удобную для отсчета или управления процессом измерения.
Лабораторные весы делятся на два вида: рычажные и пружинные. В отдельных конструкциях весов применены оба принципа.
Рычажные лабораторные весы в свою очередь, разделяются на коромысловые (двухчашечные и одночашечные) и квадрантные.
Суть
измерения массы с помощью рычажных
весов заключается в сравнении
измеряемой массы
![]() с эталонной массой гири
с эталонной массой гири
![]() .
Рычажные весы выполняют роль
компаратора, то есть устройства сравнения.
Во время операции измерения по положению
стрелки индикатора на шкале оператор
оценивает, какая из масс больше или
меньше. Схематично рычажные весы показаны
на рисунке 1.
.
Рычажные весы выполняют роль
компаратора, то есть устройства сравнения.
Во время операции измерения по положению
стрелки индикатора на шкале оператор
оценивает, какая из масс больше или
меньше. Схематично рычажные весы показаны
на рисунке 1.
Коромысло поворачивается вокруг точки соприкосновения призмы с поверхностью опорной подушки.
Условие равновесия рычажных весов состоит в равенстве нулю суммы всех действующих на вращающееся коромысло моментов:
![]()

где
![]()
![]() -
сила;
-
сила;
![]() -
расстояние от места приложения силы до
точки
-
расстояние от места приложения силы до
точки
 вращения
(точка соприкосновения призмы и
опорной подушки).
вращения
(точка соприкосновения призмы и
опорной подушки).

1 - коромысло; 2 - призма на опорной подушке; 3 - шкала; 4 - стрелка индикатора; 5 - призмы для чаш; 6 - чаши.
Рисунок 1 – Схема коромысловых равноплечих весов
Моменты
создаются минимум тремя силами: силой
тяжести гирь
![]() ;
силой тяжести объекта
;
силой тяжести объекта
![]() ,
массу которого измеряют; собственной
силой тяжести коромысла.
,
массу которого измеряют; собственной
силой тяжести коромысла.
Будем считать, что моменты, создаваемые силой тяжести коромысла, сбалансированы благодаря симметричной конструкции. Данное допущение представляет собой ошибку модели, которой в данной работе будем пренебрегать.
Тогда:
![]()
где
![]() и
и
![]() - длины плеч коромысла; 90° - угол приложения
силы к рычагу в нулевом (горизонтальном)
положении;
- длины плеч коромысла; 90° - угол приложения
силы к рычагу в нулевом (горизонтальном)
положении;
![]() - угол отклонения стрелки индикатора,
жестко связанного с коромыслом (поворота
рычага).
- угол отклонения стрелки индикатора,
жестко связанного с коромыслом (поворота
рычага).
Из приведенного выражения следует, что равновесие может наступить при любом угле , однако это создает неудобство при проведении измерений. Из практики известно, что под равновесием при взвешивании понимают установившееся горизонтальное положение коромысла.
Для получения равновесия при =0 искусственно создают некоторый противодействующий момент, который действует в направлении уменьшения угла до нуля.
Конструктивно это реализуется применением призмы и опорной подушки, показанной на рисунке 2.

а) в горизонтальном положении коромысла; б) при повороте
Рисунок 2 – Призма на опорной подушке
Реально
острие призмы не идеальное, то есть
имеет некоторый радиус закругления.
Следовательно, при повороте призма
перекатывается с одной точки опоры на
другую на некоторо е
расстояние а,
как это показано на рисунке 3. Предполагается,
что трение не позволяет призме скользить
по поверхности.
е
расстояние а,
как это показано на рисунке 3. Предполагается,
что трение не позволяет призме скользить
по поверхности.
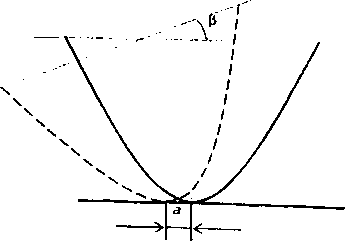
Рисунок 3 – Поворот призмы
Очевидно,
что длина плеча рычага (расстояние между
точками приложения сил) изменится на
значение смещения а.
Одно плечо
уменьшится, другое
увеличится, например
![]() и
и
![]() .
.
Аналогично происходит с призмами для чаш. Принимая смещения одинаковыми, введем общее обозначение b смещения для призм чаш.
Тогда:
![]()
Как известно, сила и масса связаны между собой прямой зависимостью:
F = mg,
где
g
- ускорение свободного падения,
индивидуальное для каждой точки
поверхности Земли, но одинаковое дл я
гири и измеряемого объекта при
взвешивании.
я
гири и измеряемого объекта при
взвешивании.
Учитывая сказанное, запишем уравнение для измеряемой массы:
![]()
Можно приближенно принять для малых углов, что смещение а и смещение b пропорциональны углу . Будем считать, что уравновешивание осуществлено так, что =0 и a=b=0.
Тогда:
![]()
Номинально
![]() следовательно
следовательно
![]() .
.
Если
уравновешивание заканчивается при
![]() ,
то это означает, что нет точного
равенства
и
,
то это означает, что нет точного
равенства
и
![]() .
Они отличаются на некоторое значение,
о котором можно судить по значению
.
Шкала отградуирована в единицах массы
пропорционально значению угла отклонения
.
Поэтому измеряемая масса:
.
Они отличаются на некоторое значение,
о котором можно судить по значению
.
Шкала отградуирована в единицах массы
пропорционально значению угла отклонения
.
Поэтому измеряемая масса:
![]()
где q- цена деления шкалы.
