1.2.Теорема Чевы в форме синусов.

В каждом из рассмотренных случаев – и в случае внутренней точки O и в случае внешней точки O- условие ( ) Чевы можно записать также в виде

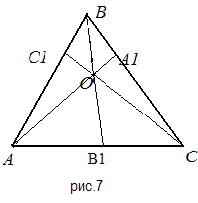
. . =1( )

Доказательство: можно воспользоваться равенствами

= = = . (1)

= = = (2)

= = = (3)

Перемножая (1), (2), (3), получаем ( ).[10, с.8].

1.3.Теорема Менелая.

Пусть на сторонах AB,BC и на продолжении стороны AC (либо на продолжениях сторон AB,BC и AC) ABC взяты соответственно точки C ,A и B , не совпадающие с вершинами ABC. Точки A ,B ,C лежат на одной прямой тогда и только тогда, когда выполняется равенство

. . =1 ( )

Доказательство:

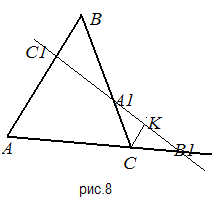
1.Необходимость. а) Пусть A ,B ,C лежат на одной прямой, причем A - на стороне BC, C -на стороне AB, B - на продолжении стороны AC за точку C.Докажем справедливость ( ). Проведем СК ll AB (рис.8).

KCB ~ C AB по I признаку, = KC= (1)

BC A ~ CKA по I признаку, = KC= (2)

Из (1) и (2) имеем = . Разделив обе части этого равенства на

, получим ( ).

П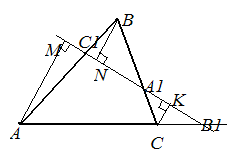 римечание 4: необходимость может быть доказана и другим способом; приведем и его, чтобы показать еще одну возможность получить подобные треугольники.

Для этого проведем перпендикуляры AM, BN, CK на

прямую C B ( рис.9).

AMC ~ BNC по I признаку, = ;

рис.9

A BN~ A CK по I признаку, = ;

CKB ~ AMB по I признаку, = .

Перемножая эти три равенства, получим . . = . . =1.

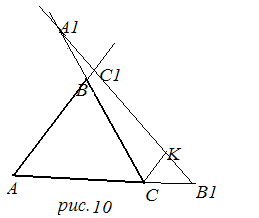
б) Рассмотрим случай, если все три точки A ,B ,C взяты на продолжениях сторон ABC,причем лежат на одной прямой. Как и в случае а), проведем CK ll AB(рис.10).

CKB ~ AC B по I признаку, = CK = ;

CKA ~ BC A по I признаку, =

CK= , тогда = =1, то есть равенство ( )

верно.

2.Достаточность. Пусть B взята на продолжении AC, точка C лежит на стороне AB, точка A - на стороне BC, причем для них выполняется . . =1( ).

Докажем, что A ,B ,C лежат на одной прямой. Заметим сначала, что . 1, так как тогда из ( ) имеем, что =1, что неверно (рис.8).Отсюда следует, что ,то есть прямые A C и AC не параллельны. Проведем через точки C и A прямую. Она пересечет прямую AC в некоторой точке B . Для точек A , C и B верна теорема Менелая, так что . . =1. Сравнивая это равенство со ( ), получаем = ; это показывает, что обе точки B и B лежат на продолжении отрезка AC за одну и ту же точку, ибо правее C данное отношение меньше 1, а левее A оно строго больше 1. Пусть CB = x , CB =y, AC=b. Тогда, учитывая, что B A=x+b, B A=y+b, перепишем полученное равенство в виде , откуда xy+xb=xy+yb, то есть x= y Из равенства CB = CB следует, что B совпадает с B , то есть A ,B ,C лежат на одной прямой [19, с.86]. Аналогично доказывается достаточность для случая, когда все три точки лежат на продолжениях соответствующих сторон.

Теорема доказана.

Эта теорема входит в золотой фонд древнегреческой математики. Она дошла до нас в арабском переводе книги « Сферика» Менелая Александрийского (I век н.э.). Равенство Менелая аналогично условию Чевы, и его можно записывать, начиная с любой вершины треугольника в любом направлении ( по часовой стрелке, против часовой стрелки).Легко заметить, что при составлении равенства надо переходить от вершины к вершине через точку пересечения секущей линии с этой стороной или ее продолжением; заканчивать необходимо в той же вершине, с которой начали.

Обозначим R= . . .Замечаем, что утверждение R=1 имеет место и в теореме Чевы, и в теореме Менелая. Поэтому справедливо следующее утверждение:

Пусть в треугольнике ABC на прямых AB,BC и AC взяты точки C ,A ,B , причем k из них лежат на сторонах треугольника и 3-k - на продолжениях сторон. Тогда

а) точки A ,B ,C лежат на одной прямой тогда и только тогда, когда R=1 и k четно (теорема Менелая);

б) прямые AA , BB и СС пересекаются в одной точке или параллельны тогда и только тогда, когда R=1 и k нечетно (теорема Чевы) [14, с.113].

Примечание 5: можно вместо отношения и других рассматривать отношения направленных отрезков, которые будем обозначать и определять следующим образом: │ │= , положительно, если векторы и одинаково направлены, и отрицательно, если они противоположно направлены ( имеет смысл только для точек, расположенных на одной прямой). Легко видеть, что отношение положительно, если точка C лежит на отрезке AB, и отрицательно, если C - вне AB.

Соответственно, вместо R будем рассматривать произведение отношений направленных отрезков, которое обозначим . Тогда

Теорема Чевы: Для того чтобы прямые AA ,BB ,CC пересекались в одной точке (или были параллельны), необходимо и достаточно, чтобы =1 [23, с.40].

Действительно, если все три точки лежат на сторонах ABC (k=3), то все три отношения в произведении будут положительными, а это значит, что =1. Если одна из точек лежит на стороне, а две другие - на продолжениях сторон треугольника, то два отношения направленных отрезков будут с минусом, и произведение снова будет равно 1.

Теорема Менелая: Для того чтобы точки A ,B ,C лежали на одной прямой, необходимо и достаточно, чтобы =-1 [23,с.41].

Действительно, если две точки лежат на сторонах треугольника, а третья - на продолжении, то одно отношение направленных отрезков отрицательно, а два – положительны; значит, произведение =-1.

Если все три точки лежат на продолжениях сторон, то все три отношения направленных отрезков будут отрицательными, следовательно, снова =-1.

Примечание 6: поскольку у школьников могут возникнуть трудности в понимании формулировки теорем, целесообразно, в зависимости от уровня учащихся, теоремы переформулировать: разделить на две – прямую и обратную.