Розділ 3 економіко-математичне моделювання та прогнозування динаміки валового внутрішнього продукту україни

3.1. Економічна постановка задачі прогнозування динаміки валового внутрішнього продукту України

Нестаціонарність макроекономічних процесів, складність їх структури, наявність біфуркаційних режимів – різкого виникнення, загасання або зміни сезонної хвилі, що може бути пов’язано з внутрішньою динамікою системи та її глибокою перебудовою, циклічність макроекономічних процесів, фрактальна структура часових рядів макроекономічних показників, а також відсутність об’ємної статистичної вибірки, унеможливлює діагностику та адекватне прогнозування динаміки макроекономічних процесів класичними методами.

У зв’язку з цим виникає необхідність застосування сучасних методів, що дозволять діагностувати та прогнозувати як незначні коливання нестаціонарних макроекономічних показників у короткостроковому періоді, так й довгострокові тенденції. Дуже важливе значення у такому сенсі набуває проблема визначення горизонту адекватного прогнозування конкретного макроекономічного показника

Важливою характеристикою ринкової економіки є її нестабільність, що проявляється в циклічній послідовності піднесень і спадів у економіці.

Теорія економічних циклів разом з теорією економічного зростання належать до теорій економічної динаміки, які пояснюють тенденції економічного розвитку. Якщо теорія зростання досліджує чинники і умови зростання як довгострокові тенденції, то теорія циклу – причини коливань економічної активності в часі. Напрям і ступінь зміни сукупності показників, що характеризують рівноважний розвиток економіки, утворюють економічну кон’юнктуру.

Для прогнозування динаміки валового внутрішнього продукту України доцільно застосовувати різні підходи, зокрема динамічні моделі з мультиплікатором (підхід Кейнса); моделі взаємодії мультиплікатора і акселератора (модель Самуельсона-Хікса).

Модель взаємодії мультиплікатора і акселератора ґрунтується на кейнсіанській концепції загальної економічної рівноваги і ілюструє вплив змін величини автономного попиту на економічну кон'юнктуру.

У моделі Кейнса встановлено, що при наявності резервних виробничих потужностей ріст автономного попиту на визначену величину збільшить національний доход на багаторазово більшу величину внаслідок ефекту мультиплікатора. Коли величина ефективного попиту перевищить наявні виробничі потужності, підприємці почнуть здійснювати індуковані інвестиції, обсяг яких визначається величиною акселератора. Індуковані інвестиції, стаючи складовою сукупного попиту, породжують черговий мультиплікаційний ефект, що знову збільшує ефективний попит і спонукує тим самим до нових індукованих інвестицій.

Повернеться економічна система до нового рівноважного стану чи ні, як розвертатиметься процес: монотонно або коливально  на ці питання дає відповідь модель мультиплікатора-акселератора (модель Самуельсона-Хікса).

Модель Самуельсона-Хікса містить у собі тільки ринок благ на тій підставі, що рівень цін, відносні ціни благ і ставка відсотка передбачаються незмінними. Відповідно до кейнсіанської концепції також передбачається, що обсяг пропозиції є досконало еластичним.

Обсяг споживання (С_t) домашніх господарств у поточному періоді t визначається величиною їхнього доходу (y_t-1) в попередньому періоді:

, (3.1)

де С₀  автономне споживання (мінімальний обсяг фонду споживання);

С₁  нижня межа фонду невиробничого споживання або гранична схильність до споживання, 0 < С₁ < 1.

Підприємці здійснюють індуковані інвестиції після того, як переконалися в тому, що збільшення сукупного попиту є стійким. Тому, приймаючи рішення про обсяг індукованих інвестицій I, вони орієнтуються на збільшення сукупного попиту (національного доходу) y_t-1 не в поточному, а в попередньому періоді:

,

де b – автономні капіталовкладення;

r – коефіцієнт акселерації (прискорення), 0 < r < 1.

При таких припущеннях економічна система буде перебувати в стані рівноваги, якщо

,

або

, (3.2)

де A_t = C₀ + b  екзогенна величина автономного попиту.

Рівняння (3.2) є неоднорідним різницевим рівнянням другого порядку, що характеризує динаміку національного доходу в часі.

При фіксованій величині автономних витрат (A_t = A = const) в економіці досягається довгострокова рівновага протягом n періодів, коли обсяг національного доходу стабілізується на визначеному рівні y^*, тобто

y_t = y_t-1 = y_t-2 = y^*,

де n  число періодів з незмінною величиною автономних витрат.

З рівняння (3.2) випливає, що .

Розглянемо характер динаміки національного доходу, якщо після досягнення довгострокової рівноваги зміниться величина автономного попиту. Для цього замінимо неоднорідне різницеве рівняння (3.2) однорідним.

Уведемо такі позначення:

y_t – y^* = Δy_t.

Значення y_t і y^* задовольняють рівність (3.2), тому можна записати таке однорідне різницеве рівняння другого порядку з постійними коефіцієнтами:

Δy_t = (С₁ + r) Δy_t-1 – r Δy_t-2, (3.3)

або

Δy_t – (С₁ + r) Δy_t-1 + r Δy_t-2 = 0. (3.4)

Напрям зміни y_t визначається напрямом зміни Δy_t, тому що y_t = y^* + Δy_t.

Для визначення загального розв’язку однорідного різницевого рівняння

Δy_t+2 + p Δy_t+1 + q Δy_t = 0,

необхідно знайти розв’язки характеристичного рівняння

² + p + q = 0.

Після цього можуть виникнути три варіанти [37].

1. Обидва корені (₁ і ₂)  дійсні і не дорівнюють один одному. Тоді загальний розв’язок має вигляд:

y_t = M₁ ,

де M₁ і M₂  довільні константи.

2. Обидва корені дійсні і дорівнюють один одному (₁ = ₂ = ), тому

y_t = (M₁+t·M₂)λ^t.

3. У випадку комплексно-спряжених коренів _1,2 = r (cos ± i sin)

y_t = r^t (M₁ cost + M₂ sint).

Отже, характер зміни Δy_t залежить від значення дискримінанта характеристичного рівняння однорідного рівняння (3.4). Оскільки в даному випадку дискримінант дорівнює (С₁ + r)² – 4r, то динаміку національного доходу визначають значення граничної схильності до споживання С₁ або мультиплікатора і акселератора r.

Якщо (С₁ + r)² – 4r > 0, то показник y_t змінюється монотонно; при (С₁ + r)² – 4r < 0 зміна y_t відбувається коливально. Отже, графік функції (С₁ + r)² = 4r, представлений на рис. 3.1, відокремлює множину елементів (r, С₁), що забезпечують монотонну зміну y_t, від множини комбінацій значень (r, С₁), що приводять до коливань y_t.

Збігатиметься значення y_t до деякої скінченої величини або розбігатиметься у нескінченність, залежить від значення останнього члену характеристичного рівняння

λ²– (С₁ + r) λ + r = 0, (3.5)

Якщо r < 1, то рівновага установиться на визначеному рівні. При r > 1 рівновага більше не відновиться у випадку її порушення. Коли r = 1, тоді значення y_t будуть коливатися з постійною амплітудою.

У результаті вся множина сполучень (r, С₁), виявилася розділеною на п'ять областей, як це показано на рис. 3.1.

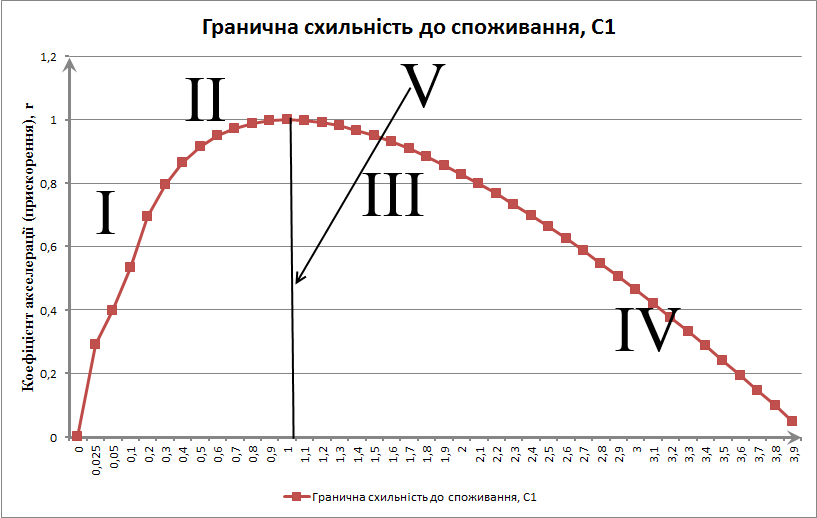
Рис. 3.1. Розподіл значень С₁ і r у залежності від їхнього впливу на характер динаміки національного доходу при зміні автономного попиту

Якщо значення (r, С₁) вказують на область I, то після порушення рівноваги в результаті зміни автономного попиту значення y_t монотонно збігатиметься до нового рівноважного рівня (рис. 3.2.а).

При значеннях (r, С₁) з області II, національний доход досягне нового рівноважного рівня, пройшовши через загасаючі коливання (рис. 3.2.б).

Множина значень (r, С₁) в області III (рис. 3.2.в), відповідають нестабільній рівновазі, динаміка y_t здобуває характеру вибухових коливань (амплітуда коливань буде збільшуватись).

Комбінації значень (r, С₁) з області IV приводять до того, що після порушення рівноваги значення y_t монотонно наближається до нескінченності (рис. 3.2.г).

І нарешті, якщо акселератор дорівнює одиниці, то при будь-якому значенні граничної схильності до споживання у випадку порушення рівноваги виникають рівномірні незатухаючі коливання y_t (рис. 3.2.д).

У реальній економіці С₁ < 1, а r > 1, тобто це області III і IV. При таких сполученнях значень граничної схильності до споживання і акселератора рівновага нестійка, і при її порушенні в моделі y_t дуже швидко приймає неправдоподібні значення. Але величина національного доходу не може істотно перевищувати величину національного доходу повної зайнятості. Це обмежує амплітуду коливань обсягу національного доходу зверху. З іншого боку, обсяг індукованих інвестицій не може бути менший від’ємної величини амортизації, і це обмежує амплітуду коливання величини національного доходу знизу.

У таких умовах збільшення автономних інвестицій приводить до коливань величини національного доходу навіть при визначенні величин С₁ і r в області IV.

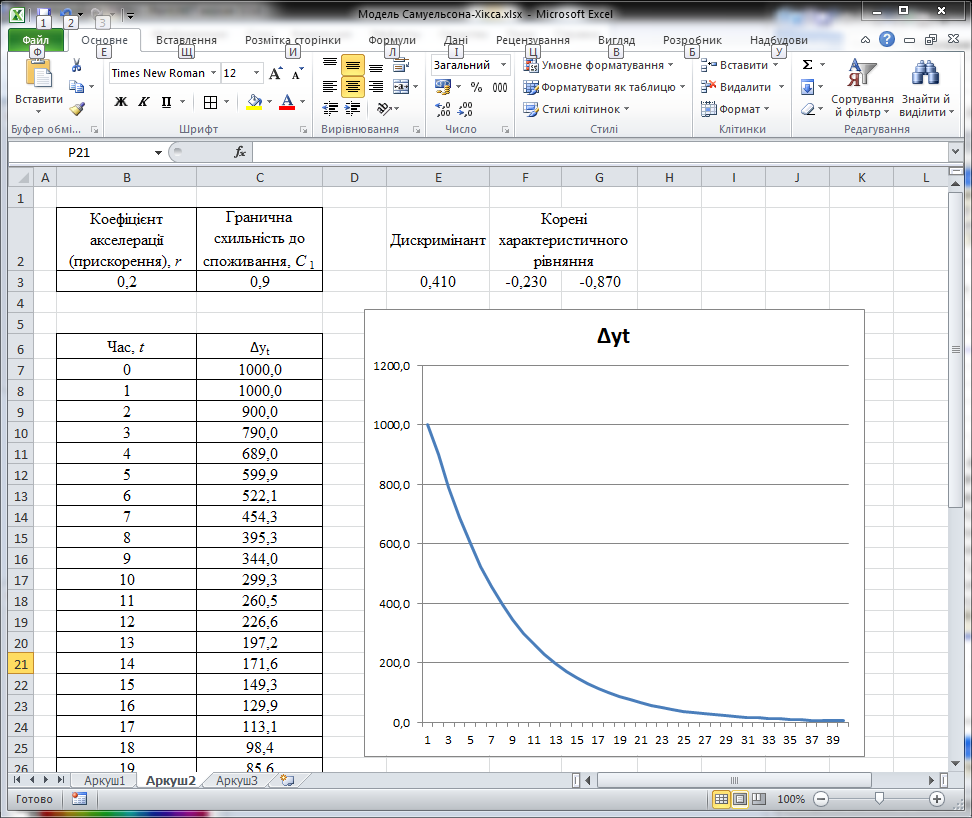
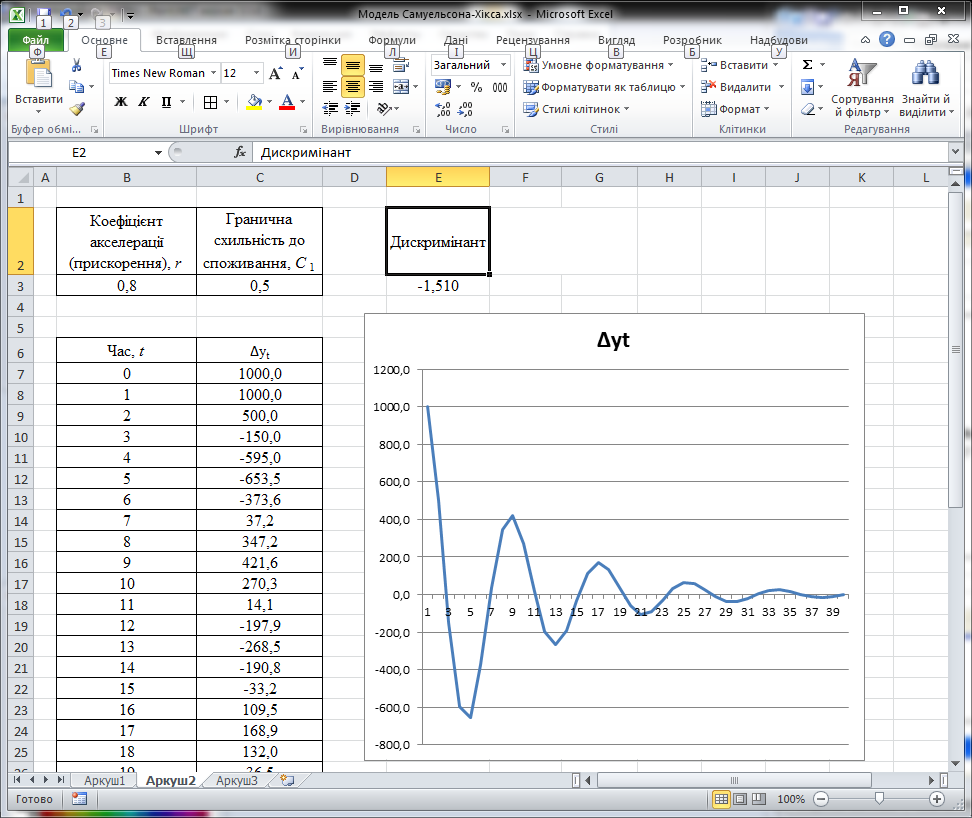
Рис. 3.2.а. Величина y_t монотонно збігається Рис. 3.2.б. Величина y_t коливально збігається

до нового рівноважного значення; до нового рівноважного значення

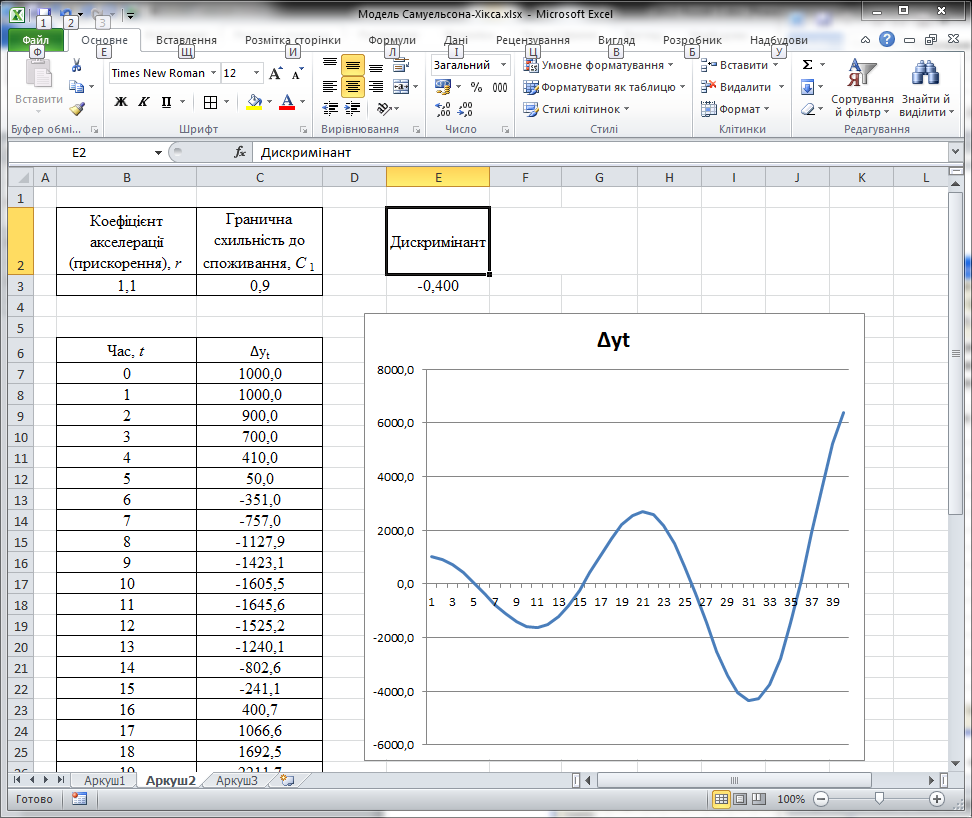
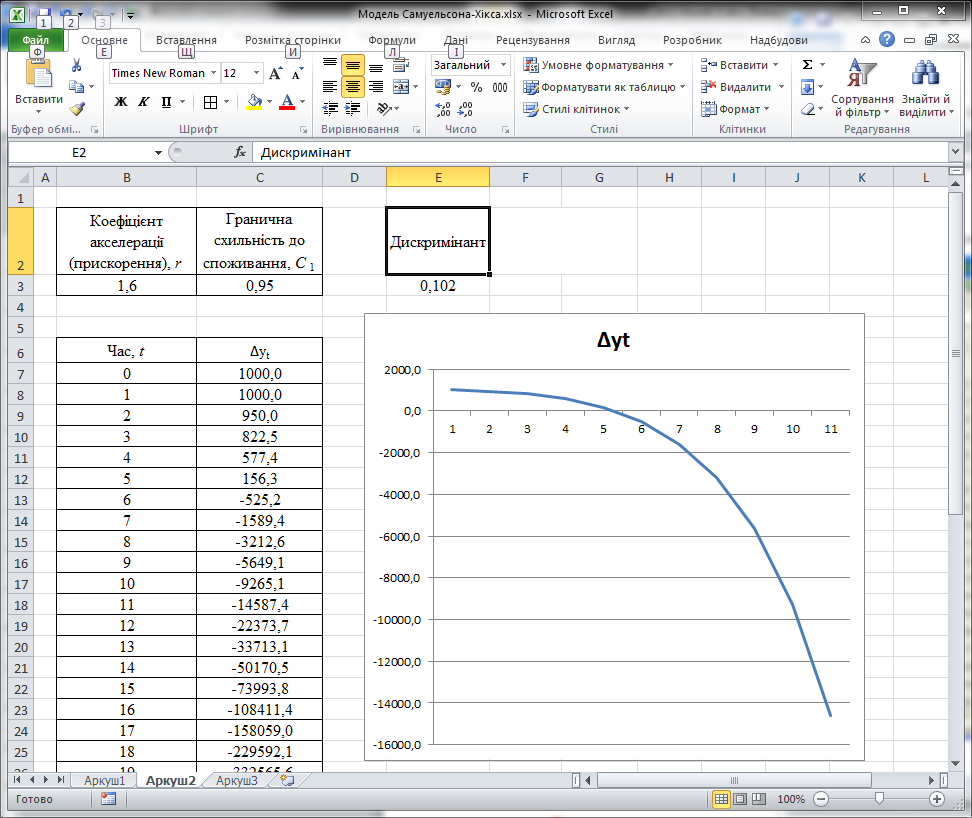
Рис. 3.2.в. Величина y_t здобуває характер вибухових коливань Рис. 3.2.г. Величина y_t монотонно спадає

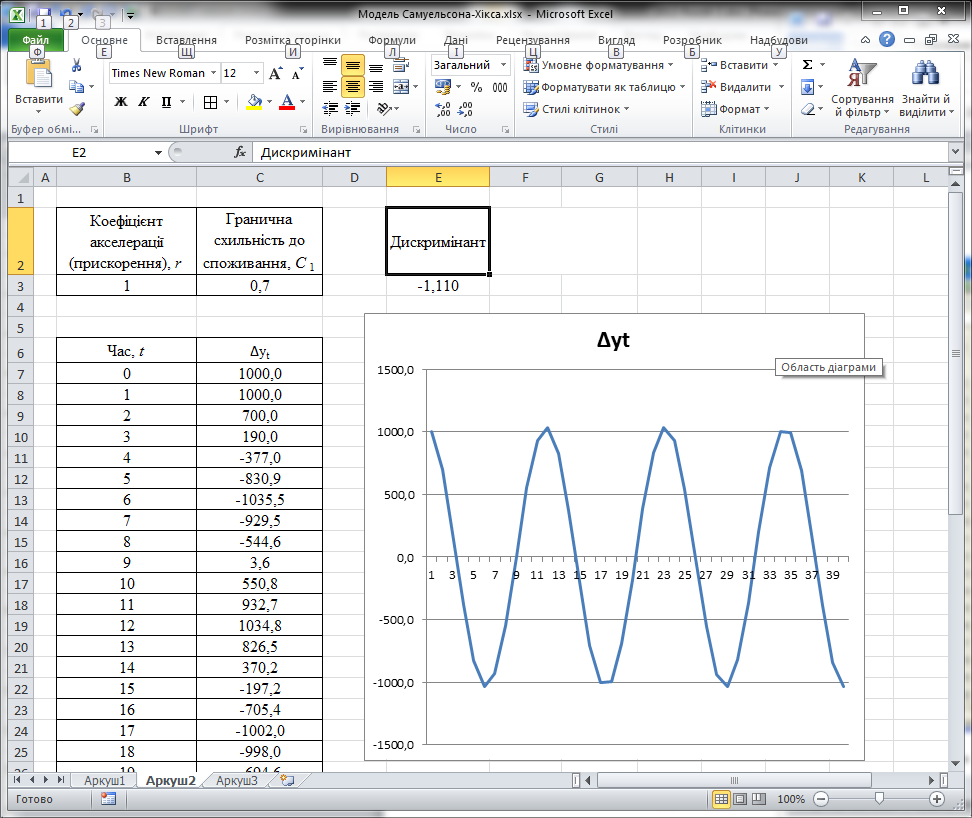
Рис. 3.2.д. Рівномірні незатухаючі коливання y_t.