3.3. Числовий приклад та аналіз отриманих результатів

На основі квартальних даних про величину валового внутрішнього продукту України з І кварталу 2002 року по IV квартал 2012 року (табл. 3.1) необхідно побудувати прогнозне значення ВВП на основі рівняння Самуельсона-Хікса.

Для усунення чітко вираженої сезонної складової величини ВВП України спочатку перейдемо до відносних величин (темпів зростання), які обчислені як відношення двох сусідніх квартальних значень ВВП. Після цього обчислимо перші та другі різниці темпів зростання ВВП y_t-4 та y_t-8 відповідно (табл. 3.2). На основі цієї таблиці знайдемо параметри моделі (3.6), а саме коефіцієнт акселерації r та граничну схильність до споживання С₁. Для оцінювання параметрів рівняння

використаємо метод найменших квадратів.

.

Таблиця 3.1.

Валовий внутрішній продукт України

Рік	Квартал	ВВП у фактичних цінах, млн.грн.	Рік	Квартал	ВВП у фактичних цінах, млн.грн.
2002	І	44132	2008	І	191 459
	ІІ	50117		ІІ	236 033
	ІІІ	65067		ІІІ	276 451
	ІV	66494		ІV	244 113
2003	І	52583	2009	І	189 028
	ІІ	60798		ІІ	214 103
	ІІІ	75812		ІІІ	250 306
	ІV	78151		ІV	259 908
2004	І	66981	2010	І	217 286
	ІІ	78607		ІІ	256 754
	ІІІ	99405		ІІІ	301 251
	ІV	100120		ІV	307 278
2005	І	88104	2011	І	257 682
	ІІ	101707		ІІ	311 022
	ІІІ	122861		ІІІ	369 818
	ІV	128780		ІV	363 557
2006	І	106348	2012	І	293 493
	ІІ	126319		ІІ	349 212
	ІІІ	152406		ІІІ	387 620
	ІV	159080		ІV	378 564
2007	І	139 444
	ІІ	166 869
	ІІІ	199 535
	ІV	214 883

Суть методу найменших квадратів полягає в тому, що пряму регресії проводять так, щоб сума квадратів відхилень фактичних значень результуючої змінної від відповідних теоретичних була найменшою:

Таблиця 3.2.

Перші та другі різниці величини ВВП України

Рік	Квартал	уt	delta yt-4	delta yt-8	Рік	Квартал	yt	delta yt-4	delta yt-8
2002	І	1	-	-	2008	І	0,89099	0,01443	0,06518
	ІІ	1,13562	-	-		ІІ	1,23281	0,03614	0,04502
	ІІІ	1,2983	-	-		ІІІ	1,17124	-0,0245	-0,0353
	ІV	1,02193	-	-		ІV	0,88302	-0,1939	-0,1608
2003	І	0,79079	-0,2092	-	2009	І	0,77435	-0,1166	-0,1022
	ІІ	1,15623	0,02061	-		ІІ	1,13265	-0,1002	-0,064
	ІІІ	1,24695	-0,0514	-		ІІІ	1,16909	-0,0021	-0,0267
	ІV	1,03085	0,00892	-		ІV	1,03836	0,15534	-0,0386
2004	І	0,85707	0,06628	-0,1429	2010	І	0,83601	0,06166	-0,055
	ІІ	1,17357	0,01734	0,03796		ІІ	1,18164	0,04899	-0,0512
	ІІІ	1,26458	0,01763	-0,0337		ІІІ	1,17331	0,00421	0,00207
	ІV	1,00719	-0,0237	-0,0147		ІV	1,02001	-0,0184	0,13698
2005	І	0,87998	0,02291	0,08919	2011	І	0,8386	0,00258	0,06425
	ІІ	1,1544	-0,0192	-0,0018		ІІ	1,207	0,02536	0,07435
	ІІІ	1,20799	-0,0566	-0,039		ІІІ	1,18904	0,01574	0,01995
	ІV	1,04818	0,04098	0,01732		ІV	0,98307	-0,0369	-0,0553
2006	І	0,82581	-0,0542	-0,0313	2012	І	0,80728	-0,0313	-0,0287
	ІІ	1,18779	0,03339	0,01422		ІІ	1,18985	-0,0172	0,00821
	ІІІ	1,20652	-0,0015	-0,0581		ІІІ	1,10998	-0,0791	-0,0633
	ІV	1,04379	-0,0044	0,0366		ІV	0,97664	-0,0064	-0,0434
2007	І	0,87657	0,05075	-0,0034
	ІІ	1,19667	0,00888	0,04228
	ІІІ	1,19576	-0,0108	-0,0122
	ІV	1,07692	0,03313	0,02874

Для оцінювання параметрів параметрів моделі (3.6) можна застосувати табличний процесор Excel.

Статистична функція ЛИНЕЙН (LINEST) розраховує статистику для динамічного ряду із застосуванням методу найменших квадратів, щоб обчислити пряму лінію, яка найкраще апроксимує наявні дані. Функція повертає масив параметрів регресії, що описує отриману пряму. Оскільки повертається масив значень, функція повинна задаватися у виді формули масиву.

Рівняння для прямої лінії має вид y=b₀+b₁x₁ або y=b₀+b₁x₁+b₂x₂+…+b_nx_n (у випадку декількох діапазонів значень x), де залежна змінна y є функцією незалежної змінної x. Значення b_і — це коефіцієнти регресії, що відповідають кожній незалежній змінні x_і (і=1,2,...,п), а b₀ — це постійна величина (вільний член рівняння регресії). Функція ЛИНЕЙН повертає масив {b_n, ..., b₂, b₁, b₀}. ЛИНЕЙН може також повертати додаткову регресійну статистику.

Синтаксис функції ЛИНЕЙН:

ЛИНЕЙН (изв_знач_y; изв_знач_x; конст; статистика).

Параметрами даної функції виступають:

1) изв_знач_y — це множина значень y, що вважаються відомі в залежності (рівнянні регресії) y=b₀+b₁x₁.

• Якщо масив изв_знач_y має один стовпець, то кожен стовпець масиву изв_знач_x інтерпретується як окрема змінна.

• Якщо масив изв_знач_y має один рядок, то кожен рядок масиву изв_знач_x інтерпретується як окрема змінна.

2) изв_знач_x — це необов'язкова множина значень x, що вважаються відомі в залежності (рівнянні регресії) y=b₀+b₁x₁.

• Масив изв_знач_x може містити одне чи кілька множин змінних. Якщо використовується тільки одна змінна, то изв_знач_y і изв_знач_x можуть мати будь-яку форму, за умови, що вони мають однакову розмірність. Якщо використовується більш однієї змінної, то изв_знач_y повинні бути вектором (тобто діапазоном висотою в один рядок або шириною в один стовпець).

• Якщо изв_знач_x не введені, то передбачається, що це масив натуральних чисел {1;2;3;...} такого ж розміру, як і изв_знач_y.

3) конст — це логічне значення, що вказує, чи потрібно, щоб константа b₀ була рівна 0.

• Якщо аргумент конст має значення „ІСТИНА” або опущена, то функція ЛИНЕЙН обчислює вільний член b₀.

• Якщо аргумент конст має значення „ФАЛЬШ”, то b₀ вважається рівним 0 і значення b₁ підбираються так, щоб виконувалася залежність y=b₁x₁ або y=b₁x₁+ b₂x_2+...+ b_пx_п .

4) статистика — це логічне значення, що вказує, чи потрібно видати додаткову статистику по регресії.

• Якщо аргумент статистика має значення „ІСТИНА”, то функція ЛИНЕЙН повертає додаткову регресійну статистику.

• Якщо аргумент статистика має значення „ФАЛЬШ” або опущена, то функція ЛИНЕЙН повертає тільки коефіцієнти b_і і вільний член b₀.

Додаткова статистика буде виводитись у такому порядку і показана в таблиці 3.3.

Точність апроксимації за допомогою прямої, обчисленої функцією ЛИНЕЙН, залежить від ступеня розкиду даних. Чим ближче дані розташовані біля прямої, тим більш точною є модель, яка використовується функцією ЛИНЕЙН. Функція ЛИНЕЙН використовує метод найменших квадратів для визначення найкращої апроксимації даних.

Таблиця 3.3.

Статистика функції ЛИНЕЙН

Коефіцієнт bn	Коефіцієнт bn-1		Коефіцієнт b2	Коефіцієнт b1	Коефіцієнт b0
Середньо- квадратичне відхилення bn	Середньо- квадратичне відхилення bn-1		Середньо- квадратичне відхилення b2	Середньо- квадратичне відхилення b1	Середньо-квадратичне відхилення b0
Крефіцієнт детермі-нації R2	Середньо- квадратичне відхилення y
F-статистика	Число ступенів свободи
Регресійна сума квадратів	Залишкова сума квадратів

Проводячи регресійний аналіз, Microsoft Excel обчислює для кожної точки квадрат різниці між теоретичним значенням і фактичним значенням y_і. Сума цих квадратів різниць називається залишковою сумою квадратів. Потім Microsoft Excel підраховує суму квадратів різниць між фактичними значеннями y_і і середнім значенням , що називається загальною сумою квадратів (загальна дисперсія), яка визначається як сума регресійної суми квадратів (пояснена регресія) і залишкової суми квадратів (непояснена дисперсія). Чим менше залишкова сума квадратів у порівнянні з загальною сумою квадратів, тим більше значення коефіцієнта детермінації R², що показує, наскільки точно рівняння, отримане за допомогою регресійного аналізу, пояснює взаємозв'язок між змінними.

Варто зауважити, що значення , які отримані за допомогою рівняння регресії, можливо не будуть адекватними, якщо вони розташовані поза інтервалом значень х, що використовувалися для визначення рівняння, тобто, потрібно обирати дані для прогнозування, які лежать в області існування регресії ( ).

Порядок обчислення за допомогою функції ЛИНЕЙН:

1. Введіть вихідні дані або відкрийте файл із даними, з якими проводиться аналіз;

2. Виділіть область порожніх комірок для виведення результатів регресійної статистики та оцінок коефіцієнтів регресії;

3. Активізувати Майстер функцій одним із способів:

• у головному меню вибрати Вставка/Функция (Insert/Function);

• на паналі інструментів Стандартная (Standart) виберіть кнопку Вставка функции (InsertFunction);

1. У вікні Категорія (Function category) вибрати Статистические (Statistical), а у вікні Функція (Function name) вибрати ЛИНЕЙН (Linest). Натисніть ОК.

2. Заповніть всі необхідні аргументи функції, .

Коли всі параметри введені, натиснути комбінацію клавіш Ctrl+Shift+Enter для автозаповнення усіх виділених клітин.

Застосувавши функції ЛИНЕЙН отримано такі параметри моделі (3.6):

коефіцієнт акселерації r=0,41602;

граничну схильність до споживання С₁=0,22671;

екзогенна величина автономного попиту A_t = 1,06104.

Модель прийме такий вигляд:

При знайдених значеннях (r, С₁), валовий внутрішній продукт досягне нового рівноважного рівня, пройшовши через загасаючі коливання (рис. 3.3). Варто зауважити, що при екзогенних шоках рівноважне значення ВВП встановиться через 10 часових періодів.

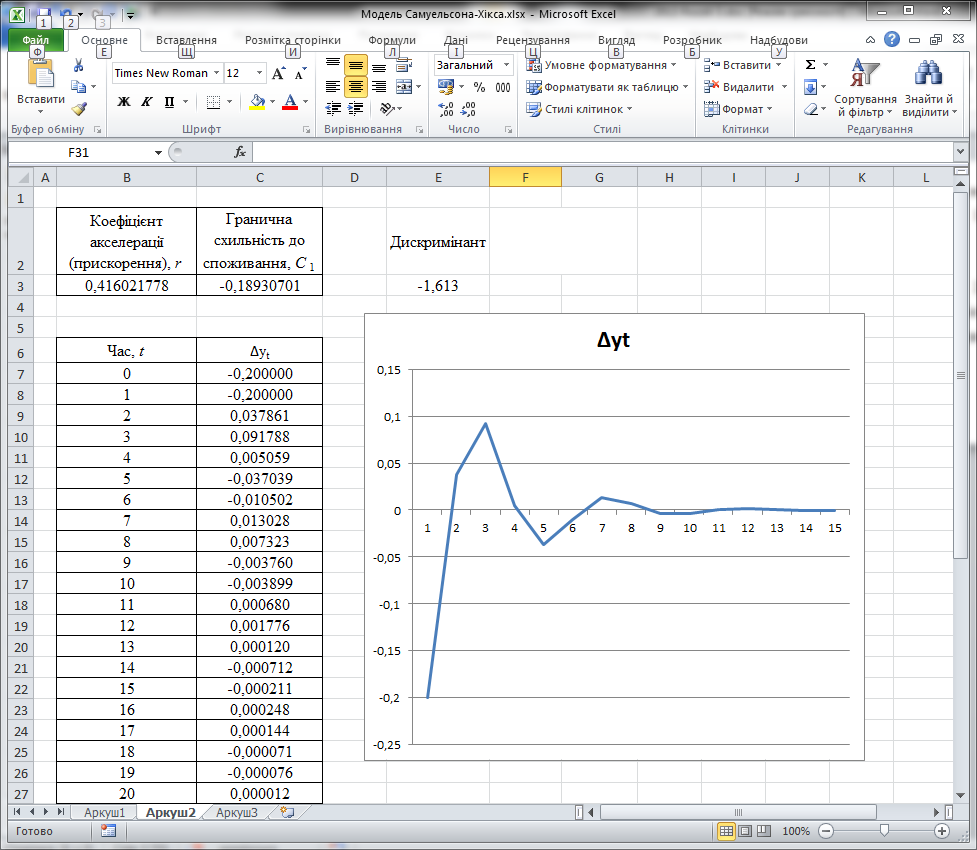
Рис. 3.3. Динаміка ВВП України

Враховуючи, що значення факторів у правій частині рівняння (3.6), відомі для , які відповідають останнім 4 кварталам, а вони у свою чергу визначають значення на рік уперед, то можна побудувати прогноз величини ВВП України на 2013 рік (табл. 3.4).

Таблиця 3.4.

Прогнозні значення ВВП України

Рік	Квартал	Темп зростання ВВП	Прогнозні значення ВВП, млн.грн.
2013	І	1,08067	317169
	ІІ	1,08808	379971
	ІІІ	1,05142	407550
	ІV	1,03658	392412

Таким чином, прогнозування економічних процесів, зокрема макроекономічних показників таких як ВВП, національний дохід, можна здійснювати за допомогою моделі Самуельсона-Хікса. Варто зауважити, що використання цієї моделі вимагає більш детального дослідження макроекономічних залежностей та врахування значної диференціації у доходах населення.