19. Основные теоремы дифференциального исчисления

1. Теорема Ферма. (О равенстве нулю производной)

Пусть функция   удовлетворяет следующим условиям:

1. она дифференцируема на интервале  ;

2. достигает наибольшего или наименьшего значения в точке  .

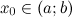Тогда производная в этой точке равна нулю, то есть  .

2. Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)

Пусть функция 

1. непрерывна на отрезке  ;

2. дифференцируема на интервале  ;

3. на концах отрезка   принимает равные значения  .

Тогда на интервале   найдется, по крайней мере, одна точка   , в которой  .

3. Теорема Лагранжа. (О конечных приращениях)

Пусть функция 

1. непрерывна на отрезке  ;

2. дифференцируема на интервале  .

Тогда на интервале   найдется по крайней мере одна точка   , такая, что

4. Теорема Коши. (Об отношении конечных приращений двух функций)

Если функции   и  :

1. непрерывны на отрезке  ;

2. дифференцируемы на интервале  ;

3. производная   на интервале  ,

тогда на этом интервале найдется по крайней мере одна точка   , такая, что

20. Правило Лопиталя для вычисления пределов функции. Раскрытие неопределённостей вида (0*∞) ; 00 ; ∞0 ; 1∞

Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть   или  . Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

21) Признаки монотонности функций. Понятие экстремума функций. Теоремы о необходимом и достаточном условиях экстремума функции.

Признаки монотонности функций.

Функция монотонна повсюду, если она непрерывна, а её производная в существует в любой точке

и не равна нулю, либо равна нулю повсюду.

Что равносильно тому, что функция повсюду возрастает, убывает или является константой.

Экстремум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Точки максимума и минимума функции называются точками экстремума.

Сформулируем теорему о необходимом условии экстремума функции: если в точке экстремума функция f(x) имеет производную, то производная равна нулю.

Отсюда следует, что точки экстремума функции следует искать среди тех точек её области определения, где производная функции равна нулю или не существует.

Точка, в которой производная равна нулю, называется стационарной.

Точки области определения функции, в которых производная либо равна нулю, либо не существует, называются критическими.

Теорема, которая называется достаточным условием экстремума.

Пусть функция f(x) непрерывна в точке x₀. Тогда:

1) если f(x) < 0 на (a;x₀) и f(x) > 0 на (x₀;b), то точка x₀ – точка минимума функции f(x);

2) если f(x) > 0 на (a;x₀) и f(x) < 0 на (x₀;b), то точка x₀ – точка максимума функции f(x);