15. Определение производной функции функции. Её геометрический и физический смысл.

Производной функции     в точке   называется предел отношения приращения функции в этой точке к приращению аргумента  ,  при  (если этот предел существует и конечен)

Физический смысл производной. 

Если  функция y = f(x) и ее аргумент x являются физическими величинами,  то производная   – скорость изменения переменной y относительно переменной x в точке .  Например, если S = S(t) – расстояние, проходимое точкой за время t,  то ее производная  – скорость в момент времени .  Если  q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени  t,  то   – скорость изменения количества электричества в момент времени , т.е. сила тока в момент времени . 2) Геометрический смысл производной.

Пусть   – некоторая кривая,  – точка на кривой  .

Любая прямая, пересекающая   не менее чем в двух точках называется секущей.

Касательной к кривой  в точке   называется предельное положение секущей   ,  если точка   стремится к  ,  двигаясь по кривой. Из определения очевидно, что если касательная к кривой в точке  существует, то она единственная. Таким образом, получили, что – угловой коэффициент касательной к графику функции y = f(x) в точке (геометрический смысл производной функции в точке).  Поэтому уравнение касательной к кривой y = f(x) в точке можно записать в виде

16. Правила и формула дифференцирования.

1) Производная константы равна нулю, т.е  , где C  – константа.2) Производная суммы (разности) равна сумме (разности) производных, т.е  3)Производная произведения находится по правилу:  .

4)  , где   - константа. 5) Производная дроби находится по правилу: .

 6) Если функция  имеет производную в точке , а функция имеет производную в точке , то сложная функция  имеет производную в точке  , причем  (правило дифференцирования сложной функции).7) Пусть функция y = f(x) имеет производную в точке , причем  .  Если существует обратная функция  , то она имеет производную в точке и   (производная обратной функции).

17. Производные высших порядков. Формулы производных n-порядка для некоторых функций. Производная от функции f¢(x) называется производной второго порядка от функции f(x) (или второй производной) и обозначается  Производная n-го порядка обозначается  Формулы: Производная n-ой степени функции y=x^а (х>0): (Х^m) ^(m)= m(m-1)(m-2)…[m-(m-1)]*1=m!, (Х^m) ⁽ⁿ⁾=0 при n>m

Производная n-ой степени функции y=a^x (0<a≠1): y⁽ⁿ⁾=a^x (lna)ⁿ В частности, если y=e^x, то для любого n (e^x)⁽ⁿ⁾=e^x

Производная n-ой степени функции y=sinx: y⁽ⁿ⁾=sin(x+n(π/2)) Аналогичная формула производной n-й степени функции y=cosx:cosx⁽ⁿ⁾=cos(x+n(π/2))

18. Понятие дифференциала функции. Приближенные вычисления с помощью дифференциала. Теоремы и свойства дифференциала функции. Дифференциалом функции y=f(x) в точке Хо называется главная, линейная относительно Δ Х , часть приращения функции в этой точке: dy=A ΔX Из определения дифференциала следует, что он зависит линейно от Ах и является главной частью приращения функции Ау. Само же Aj зависит от Ад: более сложно.  Поэтому во многих задачах приращение функции в данной точке приближенно заменяют дифференциалом функции в этой точке: ∆y=dy Абсолютная погрешность при такой замене равна │∆y-dy│ и является при ∆х→0 бесконечно малой более высокого порядка, чем ∆х. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:

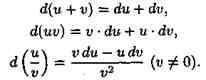
Теорема 1. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента. Пусть у=ƒ(u) и u=φ(х) две дифференцируемые функции, образующие сложную функцию у=ƒ(φ(х)). По теореме о производной сложной функции можно написать у'_х=у'_u•u'_x.