53. Угол между плоскостями.

Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.

Д вугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.

Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу

54.Параметрические уравнения прямой в пространстве

Этот вид уравнений часто применяется неожиданно.

Если известна точка , принадлежащая прямой, и направляющий вектор данной прямой, то параметрические уравнения этой прямой задаются системой:

Пряма́я — одно из фундаментальных понятий геометрии.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Согласно примеру Д. Гильберта («точкой можно назвать хоть стул»), может обозначать достаточно произвольные объекты, даже изображение которых будет зависеть от выбранной аксиоматики и/или модели геометрии.

Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.

47.Линейные операции над векторами

Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.

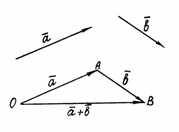
Сложение векторов. Пусть и – два произвольных вектора. Возьмем произвольную точку О и построим вектор ; затем от точки А отложим вектор . Вектор , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается (рис. 1).

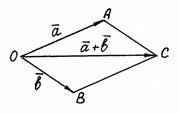
(рис.1) Ту же сумму можно получить иным способом. Отложим от точки О векторы и . Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор – диагональ параллелограмма – является суммой векторов и (рис. 2).

(рис.2) Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).

(рис.3)

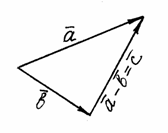
Вычитание векторов. Разностью векторов и называется такой вектор , который в сумме с вектором дает вектор : Û .

Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).

(рис.4)

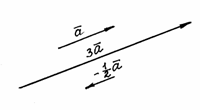
Умножение вектора на число. Произведением вектора на действительное число называется вектор (обозначают ), определяемый условиями. Построим, например, векторы и для заданного вектора (рис. 5).

(рис.5)

Понятие коллинеарных векторов.

Коллинеа́рность — отношение параллельности векторов: два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Допусти́м синоним — «параллельные» векторы.

Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Свойства линейных операций над векторами.

Сложение векторов.

Для нахождения суммы нескольких векторов можно построить ломаную из равных им векторов. Тогда замыкающий вектор, соединяющий начало первого вектора ломаной с концом последнего ее вектора, равен сумме всех векторов ломаной. На рис.1.7,в изображена сумма e четырех векторов a,b,c ,d. Таким способом (правило ломаной) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, "выстраивая цепочку" векторов для суммы в виде b+d+c+a , получим вектор, равный вектору e= b+d+c+a. Если ломаная получилась замкнутой, то сумма равна нулевому вектору.

Вычитание векторов

Вектор -a называется противоположным вектору a , если их сумма равна нулевому вектору:a+(-a)=a . Противоположный вектор имеет длину , коллинеарен и противоположно направлен вектору a. Нулевой вектор является противоположным самому себе.

Разностью векторов называется сумма вектора a с вектором b , противоположным вектору .

Умножение вектора на число

Произведением ненулевого вектора на действительное число называется вектор , удовлетворяющий условиям.

Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов , и любых действительных чисел справедливы равенства.

Свойства выражают коммутативность и ассоциативность операции сложения векторов, ещё одно свойство — ассоциативность операции умножения на число, свойства другие — законы дистрибутивности, свойство ещё очередное называется унитарностью.

Свойства линейных операций устанавливают такие же правила действия с векторами, как с алгебраическими выражениями.

41.

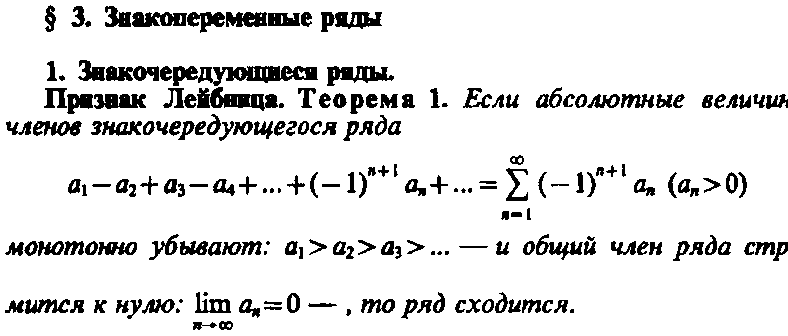
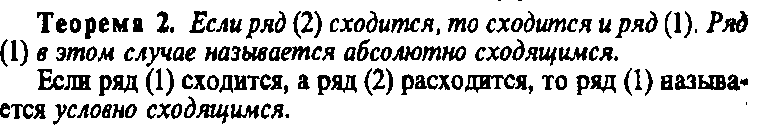
42)

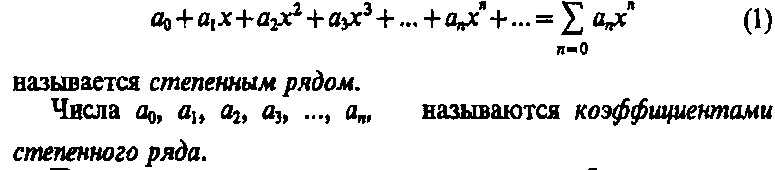
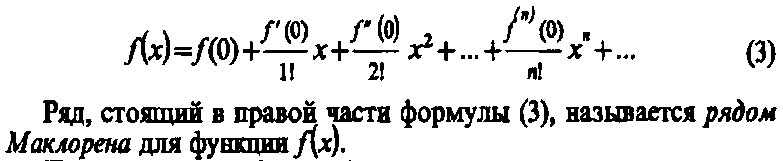
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.