36. Вычисление площадей фигур в прямоугольных координатах.

S=

где S – площадь криволинейной трапеции, ограниченной графиком трапеции, ограниченной графиком функции f(x), отрезком [a,b] на оси Ox и прямыми x=a, x=b, a<b

где S – площадь фигуры, заключенные между графиками функции f₂(x) и f₁(x), прямыми x=a, x=b, f₂(x) ≥f₁(x), a<b

.где S – площадь криволинейного сектора, ограниченной кривой, заданная в полярных координатах уравнением ρ =ρ(ɵ) , α≤ɵ≤β, и двумя полярными радиусами, составляющими с полярной осью углы α и β.

где S – площадь криволинейной трапеции, верхняя граница которой задана параметрическими x=Φ(t), y=Ψ(t), α≤Φ≤β

37. Вычисление объемов тел вращения вокруг Ox, Oy, поверхностей тел вращения в прямоугольных координатах.

Вращение по оси x

Объём тела, образуемого вращением вокруг оси   фигуры, ограниченной функцией   на интервале  , осью   и прямыми   и   равен:

Дифференциал переменного объема dV=πx²dy

Вращение по оси. Объём тела, образуемого вращением вокруг оси   фигуры, ограниченной функцией   на интервале  , осью   и прямыми   и   равен:

Дифференциал переменного объема dV=πy²dx

Формулы площадей поверхностей вращения.

где S — площадь поверхности, образованной вращением кривой, заданной уравнением y=f(x), a≤x≤b, вокруг оси Ох.

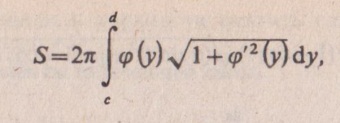
где S — площадь поверхности, образованной вращением кривой, заданной уравнением х = Φ(у), c≤y≤d, вокруг оси Оу.

где S — площадь поверхности, образованной вращением кривой, заданной параметрическими уравнениями x=Φ (t), у = Ψ(t), α≤t≤β

где S — площадь поверхности, образованной вращением кривой, заданной уравнением в полярных координатах р = р(Φ),

α≤t≤β

38. Вычисление длины дуги в прямоугольных координатах.

Пусть функция f(x) непрерывно дифференцируема на [a,b], тогда длина дуги кривой   на указанном промежутке вычисляется по формуле: . (4.7) Если кривая гладкая и задана параметрически, то длина дуги этой кривой при   вычисляется по формуле: . (4.8) Если гладкая кривая задана в полярных координатах   и  , то длина ее дуги равна . 

39. Понятие числового ряда.Необходимые признак сходимости числового ряда

40. Достаточные признаки сходимости ряда.

48.Скалярным произведением двух не нулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

Сли хотя бы один из векторов или равен нулевому вектору, то .

Свойства скалярного произведения:

1°    - симметричность.

2°    . Обозначается и называется скалярный квадрат.

3°    Если , то

4°    Если и и , то . Верно и обратное утверждение.

5°   

6°   

7°   

Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат.

49Векторное произведение двух векторов а и b – это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами: Лиже его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма .

50

Смешанным произведением трех векторов , , называется число, равное скалярному произведению вектора на вектор :

Свойства смешанного произведения:

1°   

2

3°    Три вектора компланарны тогда и только тогда, когда

4°    Тройка векторов является правой тогда и только тогда, когда . Если же , то векторы , и образуют левую тройку векторов.

5°   

6°   

7°   

8°   

9°   

10°   ТождествоЯкоби:

Если векторы , и заданы своими координатами, то их смешанное произведение вычисляется по формуле

61.Решение дифференциальных уравнений первого порядка с разделяющимися переменными.

Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

где p(x) и h(y) − непрерывные функции. Рассматривая производную y' как отношение дифференциалов , перенесем dx в правую часть и разделим уравнение на h(y):

Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x₀, при котором h(x₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения. Обозначив , запишем уравнение в форме:

Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

где C − постоянная интегрирования. Вычисляя интегралы, получаем выражение

описывающее общее решение уравнения с разделяющимися переменными.

62. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Способы их решения.Однородные дифференциальные уравнения 1-го порядка.

Определение 1. Уравнение 1-го порядка называется однородным, если для его правой части при любых справедливо соотношение , называемое условием однородности функции двух переменных нулевого измерения.

Пример 1. Показать, что функция - однородная нулевого измерения.Решение.

, Что и требовалось доказать.

Теорема. Любая функция - однородна и, наоборот, любая однородная функция нулевого измерения приводится к виду .

Определение 2. Уравнение (4.1)

В котором M И N – однородные функции одной и той же степени, т. е. обладают свойством при всех , называется однородным. Очевидно, что это уравнение всегда может быть приведено к виду (4.2) , хотя для его решения можно этого и не делать.

Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены искомой функции Y по формуле Y=Zx, Где Z(X) – новая искомая функция. Выполнив эту подстановку в уравнении (4.2), получим: или или .

Интегрируя, получаем общий интеграл уравнения относительно функции Z(X) , который после повторной замены дает общий интеграл исходного уравнения. Кроме того, если - корни уравнения , то функции - решения однородного заданного уравнения. Если же , то уравнение (4.2) принимает вид

и становится уравнением с разделяющимися переменными. Его решениями являются полупрямые: .

Линейные дифференциальные уравнения 1-го порядка. Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:

, (7.1) Где P(X) И Q(X) – заданные непрерывные функции от X. Если функция , То уравнение (7.1) имеет вид: (7.2) И называется линейным однородным уравнением, в противном случае оно называется линейным неоднородным уравнением. Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:

(7.3) Выражение (7.3) есть общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция P(X) обозначает ту же функцию, что и в уравнении (7.2), применим прием, называемый методом вариации произвольной постоянной и состоящий в следующем: постараемся подобрать функцию С=С(X) Так, чтобы общее решение линейного однородного уравнения (7.2) являлось бы решением неоднородного линейного уравнения (7.1). Тогда для производной функции (7.3) получим:

. Подставляя найденную производную в уравнение (7.1), будем иметь:

Или .Откуда , где - произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет (7.4) Первое слагаемое в этой формуле представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое формулы (7.4) есть частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при . Этот важный вывод выделим в виде теоремы. Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения , то все остальные решения имеют вид , где - общее решение соответствующего линейного однородного дифференциального уравнения. Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде . Тогда . Подставим найденную производную в исходное уравнение: . Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию U(X) за скобку: (7.5) Потребуем обращения в нуль круглой скобки: . Решим это уравнение, полагая произвольную постоянную C равной нулю: . С найденной функцией V(X) вернемся в уравнение (7.5): . Решая его, получим: . Следовательно, общее решение уравнения (7.1) имеет вид:

.

63. Дифференциальные уравнения второго порядка. Общие понятия. Решение дифференциальных уравнений, допускающих понижение порядка.

Дифференциальное уравнение 2-го порядка имеет вид: . (1.1) Общим решением уравнения является семейство функций, зависящее от двух произвольных постоянных и : (или – общий интеграл дифференциального уравнения 2-го порядка). Задача Коши для дифференциального уравнения 2-го порядка (1.1) состоит в отыскании частного решения уравнения, удовлетворяющего начальным условиям: при : , . Необходимо заметить, что графики решений уравнения 2-го порядка могут пересекаться в отличие от графиков решений уравнения 1-го порядка. Однако решение задачи Коши для уравнений 2-го порядка (1.1) при довольно широких предположениях для функций, входящих в уравнение, единственно, т.е. всякие два решения с общим начальным условием , совпадают на пересечении интервалов определения.

Уравнения, допускающие понижение порядка.

64. Линейные однородные дифференциальные уравнения второго порядка.Линейные однородные дифференциальные уравнения

   Определение. Дифференциальное уравнение n-го порядка называется линейным, если оно первой степени относительно совокупности искомой функции у и ее производных у', ..., y⁽ⁿ⁾, т. е. имеет вид

y⁽ⁿ⁾ + a₁(x) y^(n-1) + … + a_n(x) y = 0, (1)

где а₀(x), а₂(x), ..., а_n(x) - заданные функции от х или постоянные, причем а₀(x) ≠ 0 для всех значений х из той области, в которой мы рассматриваем уравнение (1). В дальнейшем мы будем предполагать, что функции а₀(x), а₂(x), ..., а_n(x) непрерывны при всех значениях х, причем коэффициент а₀ = 1 (если он не равен 1, мы можем все члены уравнения поделить на него).    Теорема 1. Если y = y₁ есть решение уравнения (1), то y = c·y₁ является тоже решением уравнение (1), где с — произвольная постоянная.       Теорема 2. Если y₁ и y₂  является решением уравнения (1) то y = y₁ + y₂ есть тоже решение уравнения (1). 65 Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Структура общего решения

Линейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y₀(x) соответствуюшего однородного уравнения и частного решения y₁(x) неоднородного уравнения:

Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.

Метод вариации постоянных. Если общее решение y₀ ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:

Вместо постоянных C₁ и C₂ будем рассматривать вспомогательные функции C₁(x) и C₂(x). Будем искать эти функции такими, чтобы решение

удовлетворяло неоднородному уравнению с правой частью f(x). Неизвестные функции C₁(x) и C₂(x) определяются из системы двух уравнений:

Метод неопределенных коэффициентов

Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

1. 

2. где P_n(x) и Q_m(x) − многочлены степени n и m, соответственно.

В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель x^s, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.

Принцип суперпозиции

Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида

то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

66 Случайное событие, операции над событиями Случайные события и их классификация, операции над событиями. Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий. Достоверным называется событие W, которое происходит в каждом опыте. Невозможным называется событие Æ, которое в результате опыта произойти не может. Несовместными называются события, которые в одном опыте не могут произойти одновременно. Суммой (объединением) двух событий A и B (обозначается A+B, AÈB) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно. Произведением (пересечением) двух событий A и B (обозначается A×B, AÇB) называется такое событие, которое заключается в том, что происходят оба события A и B вместе. Противоположным к событию A называется такое событие , которое заключается в том, что событие A не происходит.

События A_k (k=1, 2, ..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.

При преобразовании выражений можно пользоваться следующими тождествами:

.

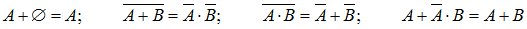67 Классическое определение вероятности

Вероятностью события называется отношение числа исходов , благоприятствующих его наступлению к числу всех исходов (несовместных, единственно возможных и равновозможных):.

Будем различать достоверные и невозможные события. По определению, их вероятности соответственно равны 1 и 0.

68 Относительная частота события. Статистическое определение вероятности

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу практически произведенных испытаний. Таким образом, относительная частота А определяется формулой:

(2)где m-число появлений события, n-общее число испытаний.

Сопоставляя определение вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.

В качестве статической вероятности принимают относительную частоту или число, близкое к ней.

Число, к которому стремится устойчивая относительная частота, называется статистической вероятностью этого события.

69 Теорема сложения вероятностей Суммой событий и называется событие , состоящее в наступлении, по крайней мере, одного из событий или , т. е. в наступлении события , или события , или обоих этих событий вместе, если они совместны. Теорема. Вероятность суммы двух несовместных событий и равна сумме вероятностей этих событий: .

70 Теорема умножения вероятностей Произведением событий и называется событие , состоящее в том, что в результате испытания произошло и событие , и событие , т. е. оба события произошли. Два события и называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события и называются зависимыми. Теорема. Вероятность произведения двух независимых событий и равна произведению этих вероятностей: .

71.

(формула полной вероятности). Пусть — полная группа событий. Тогда вероятность любого события может быть вычислена по формуле:

(формула Байеса(1)). Пусть — полная группа событий, и — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие , если в результате эксперимента наблюдалось событие , может быть вычислена по формуле:

72.

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;

2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. http://www.matburo.ru/tv/tvbook/par_1_7.files/image002.gif , а вероятность противоположного события (событие А не наступило) - буквой .

http://www.matburo.ru/tv/tvbook/par_1_7.files/image004.gif

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

http://www.matburo.ru/tv/tvbook/par_1_7.files/image006.gif

Распределение числа успехов (появлений события) носит название биномиального распределения

Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) имеет вид:

Так как np – q = np – p - 1, то эти границы отличаются на 1. Поэтому k, являющееся целым числом, может принимать либо одно значение, когда np целое число (k = np) , то есть когда np + p (а отсюда и np - q) нецелое число, либо два значения, когда np -q целое число.

73.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.

Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.

Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) = 1 - р = q.

Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:

где pn - вероятность того, что при n испытаниях событие А наступит n раз;

qn - вероятность того, что при n испытаниях событие А не наступит ни разу;

вероятность того, что при n испытаниях событие А наступит m раз, а событие Ā наступит n-m раз;

- число сочетаний (комбинаций) появления события А и Ā.

74.

ОПРЕДЕЛЕНИЕ. Функцией распределения называют функцию , определяющую вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х, т.е.

F(x)=P(X<x)

Иногда вместо термина «Функция распределения» используют термин «Интегральная функция».

Свойства функции распределения:

1. Значения функции распределения принадлежит отрезку [0;1]: 0F(x)1

2. F(x) - неубывающая функция, т.е. F(x2) F(x1), если x2>x1

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a,b), равна приращению функции распределения на этом интервале:

P(aX<b)=F(b)-F(a)

Функция распределения вероятностей

Непрерывную случайную величину нельзя охарактеризовать перечнем всех возможных ее значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин.

Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е.

F(x) = P (X <x).

Иногда функцию F(x) называют интегральной функцией распределения.

Функция распределения обладает следующими свойствами:

1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1.

2. Функции распределения есть неубывающая функция.

3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:

Р(а < X < b) = F(b) – F(а). (2.1)

4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то

F(x) = 0 при х ≤ а; F(x) = 1 при х ≥ b.

5. Справедливы следующие предельные отношения:

http://math.immf.ru/img/712.gif.

Для дискретной случайной величины Х, которая может принимать значения х1, х2, …,хn, функция распределения имеет вид

http://math.immf.ru/img/712.gif

где неравенство под знаком суммы означает, что суммирование касается всех тех значений хi, величина которых меньше х.

Поясним эту формулу исходя из определения функции F(x). Предположим, что аргумент х принял какое-то определенное, но такое, что выполняется неравенство xi<x≤xi+1. Тогда левее числа х на числовой оси окажутся только те значения случайной величины, которые имеют индекс 1, 2, 3, …, i. Поэтому неравенство Х<x выполняется, если величина Х примет значения хк, где k = 1, 2, …, i. Таким образом, событие Х<x наступит, если наступит любое, неважно какое, из событий Х = х1, Х=х2, Х=х3, …, Х=хi. Так как эти события несовместны, то по теореме сложения вероятностей имеем

http://math.immf.ru/img/713.gif . (2.2)

Предположим теперь, что для непрерывной случайной величины Х ее функция распределения F(x) имеет непрерывную производную

F'(x)= φ(x).

Функцию φ(x) называют плотностью вероятности (для данного распределения) или дифференциальной функцией.

Так как плотность вероятности φ(x) является производной неубывающей функции F(x), то она неотрицательна: φ(x)≥0. В отличие от функции распределения, плотность вероятности может принимать сколь угодно большие значения.

Так как F(x) является первообразной для φ(x), то на основании формулы Ньютона-Лейбница (http://math.immf.ru/img/714.gif)имеем . Отсюда получаем

P(a ≤ X ≤ b) = http://math.immf.ru/img/715.gif . (2.3)

Полагая а=–∞ и b=+∞, получаем достоверное событие Х принадлежащее (–∞, +∞), вероятность которого равна единице. Следовательно,

http://math.immf.ru/img/716.gif .

В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то http://math.immf.ru/img/717.gif. Полагая в формуле а = –∞, b = х и обозначая для ясности переменную интегрирования t, получим функцию распределения

F(x) = P(– ∞ < X < x) =

Одним из наиболее часто встречающихся распределений является нормальное распределение. Оно играет большую роль в теории вероятностей и занимает среди других распределений особое положение. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях.

Если предоставляется возможность рассматривать некоторую случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения. Суммируемые случайные величины могут подчиняться каким угодно распределениям, но при этом должно выполняться условие их независимости (или слабой зависимости). При соблюдении некоторых не очень жестких условий указанная сумма случайных величин подчиняется приближенно нормальному закону распределения и тем точнее, чем большее количество величин суммируется.

Ни одна из суммируемых случайных величин не должна резко отличаться от других, т. е. каждая из них должна играть в общей сумме примерно одинаковую роль и не иметь исключительно большую по сравнению с другими величинами дисперсию.

Определение: Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

http://apollyon1986.narod.ru/docs/TViMS/NP/lekziitv/lek156.gif

где а и s—некоторые постоянные, называемые параметрами нормального распределения.

Свойства.

1°. Областью определения функции f(x) является вся числовая ось.

2°. Функция f{x) может принимать только положительные значения, т. е. f(x}>0.

3°. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции.

4°. Функция f{x) имеет в точке х = a максимум, равный

http://apollyon1986.narod.ru/docs/TViMS/NP/lekziitv/lek160.gif

5°. График функции f(x) симметричен относительно прямой х = а.

6°. Нормальная кривая в точках х = а +s имеет перегиб,

76.

Закон распределения полностью характеризует дискретную случайную величину. Однако, когда невозможно определить закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины:

1. Математическое ожидание,

2. Дисперсия,

3. Среднее квадратичное отклонение

Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.

Математическое ожидание M дискретной случайной величины - это среднее значение случайной величины, равное сумме произведений всех возможных значений случайной величины на их вероятности.

Свойства математического ожидания:

Математическое ожидание постоянной величины равно самой постоянной

Постоянный множитель можно выносить за знак математического ожидания

Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий

Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых

Дисперсия случайной величины — мера разброса случайной величины, равная математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания.

Принимая во внимание свойства математического ожидания, легко показать что

Свойства дисперсии:

Дисперсия постоянной равна нулю.

Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

Если x и y независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий.

Средним квадратическим отклонением случайной величины (иногда применяется термин «стандартное отклонение случайной величины») называется число равное

77.

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл

http://pgsksaa07.narod.ru/examples_neprer_vel/theory/th_31.gif.

Если возможные значения принадлежат всей числовой оси, то

http://pgsksaa07.narod.ru/examples_neprer_vel/theory/th_32.gif

(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные непрерывной случайной величины X принадлежат отрезку [a,b], то

http://pgsksaa07.narod.ru/examples_neprer_vel/theory/th_33.gif.

Если возможные значения принадлежат всей числовой оси, то

http://pgsksaa07.narod.ru/examples_neprer_vel/theory/th_34.gif

(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).

Средним квадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии:

78.

Числовые характеристики биноминального распределения:

М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях;

D(m)=npq - дисперсия частоты появления события. А;

- среднее квадратическое отклонение частоты.

Математическое ожидание характеризует центр рассеивания значений случайной величины и при изменении µ кривая будет смещаться вдоль оси абсцисс. Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь. Таким образом, параметр µ характеризует положение, а параметр σ²- форму кривой плотности вероятности.

79.

Генеральной совокупностью называют совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений случайной величины, или совокупность результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов.

Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки.

Выборка — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.

Характеристики выборки:

1. Качественная характеристика выборки – что именно мы выбираем и какие способы построения выборки мы для этого используем.

2. Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

80.

Под термином “оценка” в теории оценок понимаются как сами значения параметров генеральной совокупности, полученные по выборке, так и процесс получения этих значений, т. е. правило, по которому они получены.

Оценки подразделяются на два класса; точечные и интервальные.

Точечные оценки представляют собой определенные значения параметров генеральной совокупности, полученные по выборочным данным. Эти значения должны быть максимально близки к значениям соответствующих параметров генеральной совокупности, которые являются истинными значениями оцениваемых параметров.

При формировании интервальных оценок определяют границы интервалов, между которыми с большой вероятностью находятся истинные значения параметров.

Начнем с точечных оценок и рассмотрим оценку произвольного параметра (среднего, дисперсии или какого-то другого) генеральной совокупности, который обозначим a. Оценивая параметр a по выборке, находим такую величину aВ, которую принимаем за точечную оценку параметра a. Естественно, при этом стремимся, чтобы оценка была в определенном смысле наилучшей, поэтому к ней предъявляется ряд требований:

1. Состоятельность. Точечная оценка aВ называется состоятельной, если при неограниченном увеличении объема выборки (n→∞) она стремится к истинному значению параметра a.

В математической статистике показывается, что состоятельной оценкой генерального среднего значения µ, является выборочное среднее арифметическое

http://bars-minsk.narod.ru/stud/VM/lecture3.files/image006.gif, а состоятельной оценкой генеральной дисперсии σ² — выборочная дисперсия

3. Несмещенность. Оценка aВ называется несмещенной, если она не содержит систематической ошибки, т. е. среднее значение оценки, определенное по многократно повторенной выборке объема n из одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра a.

Выборочное среднее арифметическое является несмещенной оценкой генерального среднего µ.

Несмещенной оценкой генеральной дисперсии σ² является исправленная выборочная дисперсия, вычисляемая по формуле

- для несгруппированных данных,

- для сгруппированных данных

3. Эффективность. Несмещенная оценка является эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещенными оценками того же параметра генеральной совокупности.

Это надо понимать так: полученные по выборке оценки и S² — случайные величины, так как случайны сами выборочные значения. Поэтому можно говорить о математическом ожидании и дисперсии оценок и S². Эффективность этих оценок означает, что их дисперсии D( ) и D(S2) меньше дисперсий любых других несмещенных оценок среднего значения и дисперсии генеральной совокупности.

Итак, наилучшими в указанном смысле оценками генерального среднего значения и генеральной дисперсии являются выборочные характеристики , S².

Выборочное среднее как точечная оценка математического ожидания.

Оценки и S², полученные по выборке, естественно не совпадают с истинными значениями параметров µ и σ² генеральной совокупности. Экспериментально проверить это утверждение невозможно, поскольку не известны истинные значения этих параметров. Но если брать повторные выборки из одной и той же генеральной совокупности с параметрами µ и σ² и каждый раз вычислять их оценки и S², то окажется, что эти оценки для разных выборок не совпадают, хотя все это из одних и тех же генеральных параметров.

Отклонения оценок генеральных параметров от истинных значений этих параметров называются статистическими ошибками, или ошибками репрезентативности. Их происхождение не имеет ничего общего с ошибками измерения, а возникают они только потому, что не все объекты генеральной совокупности представлены в выборке.

Величины статистических ошибок оценивают по среднему квадратическому (стандартному) отклонению выборочных характеристик. Здесь рассматривается только стандартное отклонение выборочного среднего арифметического.

Если взять очень много независимых выборок объема n из одной и той же генеральной совокупности и определить для каждой из них среднее арифметическое, то окажется, что полученные средние арифметические варьируют вокруг своего среднего значения (равного µ ) в раз меньше, чем отдельные варианты выборки. Т.е. стандартное отклонение выборочного среднего арифметического будет равно

где σ— стандартное отклонение генеральной совокупности.

В качестве оценки стандартного отклонения выборочного среднего используется величина

(5.1)

называемая стандартной ошибкой среднего арифметического. В формуле (5.1) S — выборочное стандартное отклонение

Величина показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего µ его выборочную оценку . Поэтому вычисленное среднее арифметическое часто указывают в виде

чтобы оценить точность оценки х.

Из формулы (5.1) видно, как зависит стандартная ошибка от объема выборки n: с увеличением объема выборки n стандартная ошибка уменьшается пропорционально корню квадратному из n.