32. Интегрирование иррациональных функций.

1. Интеграл вида , где a, b, c, d некоторые числа ; m – натуральное число, R – рациональная функция от x и от . Такой интеграл рационализируется подстановкой .

, , ,

,

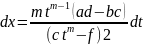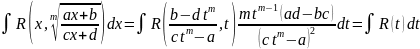Где R(t) – рациональная функция аргумента t

2. Интеграл вида 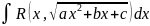, где a, b, c – некоторые числа; a≠ 0; R – рациональная функция от x и от .

Если трехчлен имеет вешественные корни x_{1 ,} x₂ (x₁≠, x₂) и a>0, то

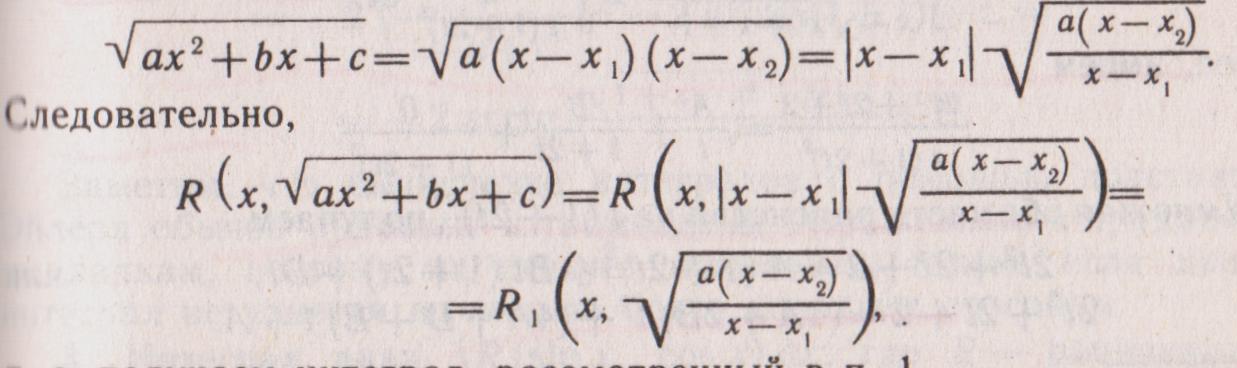
Т.е. получаем интеграл, рассмотренный в п.1.

Если x₁ = x₂ , то

Т.е. под знаком интеграла находится рациональная функция от x.

Когда трехчлен ax² + bx+ c вещественных корней и а>0. Покажем, что в данном случае интеграл рационализируется подстановкой Эйлера

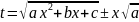
Возводя обе части равенства в квадрат, получаем bx+c=t²-2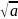 tx, так что

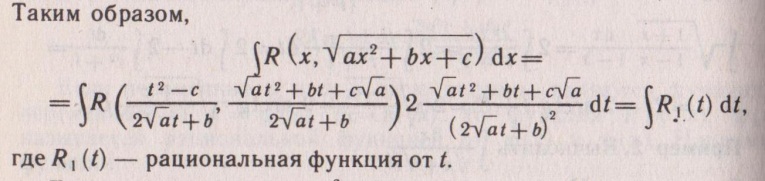
Если же в трехчлене ax²+bx+c a<0, а c>0, то для рационализации интеграла можно применить другую подстановку Эйлера.

33.Интегрирование некоторых трансцендентных функций

1. Интеграл вида , где R – рациональная функция от sinx и от cosx. Интеграл рациональной подстановки

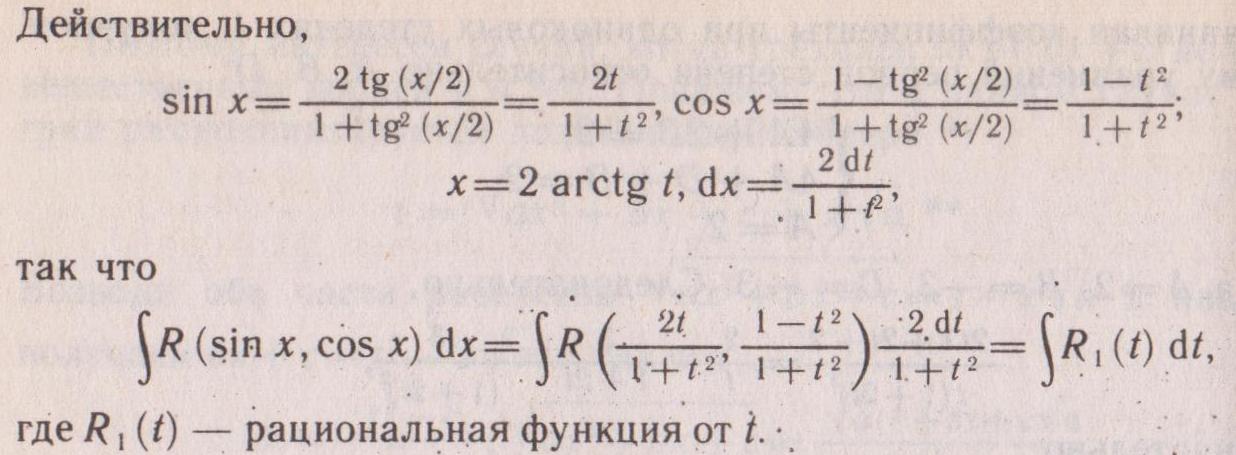
2. Интеграл вида 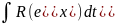. Данный интеграл рационализуется подстановкой

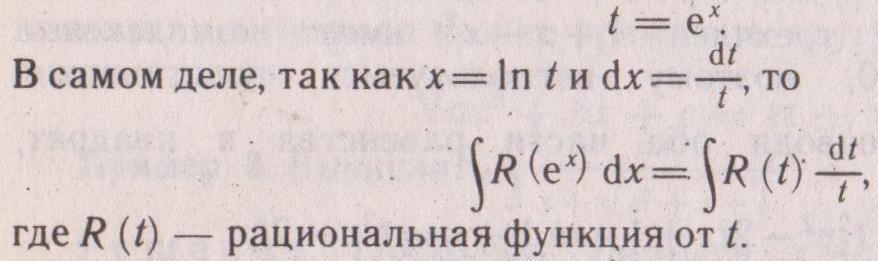
34. Понятие определенного интеграла. Его свойства.

Если существует конечный предел I интеграль­ной суммы при λ-›0, то этот предел называется определенным интегралом от функции f(x) по отрезку [а, Ь] и обозначается следующим образом:

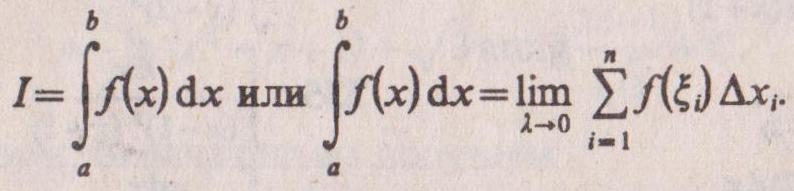
В этом случае функция f(х) называется интегрируемой на [а, b]. Числа а и b называются соответственно нижним и верхним пределами интегрирования, f(х) — подынтегральной функцией, х — переменной интегрирования.

Для интегрируемости функции достаточно ее непрерывности на отрезке [а, b].Основные свойства определенного интеграла.

1°. По определению 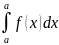=0

2°. По определению

3°. Каковы бы ни были числа а, b, с, всегда имеет место равенство

4°. Постоянный множитель можно выносить за знак определенного интеграла, т. е.

5°. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т. е.

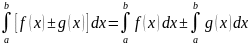
Формула Ньютона—Лейбница. Если функция f(x) непреры­вна на отрезке [а, b] и функция F(x) является некоторой ее первообразной на этом отрезке, то имеет место формула Ньюто­на—Лейбница

35. Понятие несобственного интеграла первого и второго рода.

Несобственные интегралы с бесконечными пределами интегрирования. По определению,

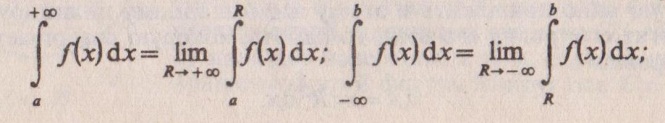
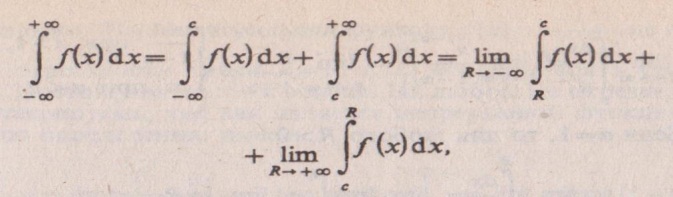где С — любое число. Если приведенные пределы существуют и конечны, то их называют несобственными интегралами первого рода. В этом случае соответствующие интегралы называют сходящимися. В противном случае — расходящимися.

Несобственные интегралы от неограниченных функций. Если функция f(х) определена на промежутке [а, b), интегрируема на любом отрезке [а, b — ę], заключенном в [а, b), и не ограничена слева от точки b (ее называют особой), то, по определению,

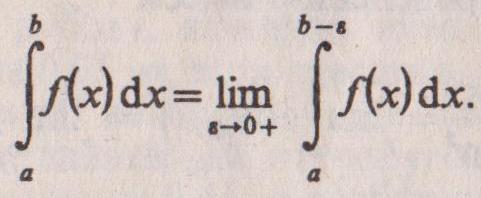Если этот предел существует и конечен, то его называют несобственным интегралом второго рода, а интеграл называется сходящимся. В противном случае — расходящимся.