28)Таблица интегралов.

29)Интегрирование некоторых тригонометрических функций.

Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

Интеграл вида .

Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

,

Тогда

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой.

Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

Интеграл вида если

функция R является нечетной относительно cosx.

Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.

Функция может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.

Интеграл вида если

функция R является нечетной относительно sinx.

По аналогии с рассмотренным выше случаем делается подстановка t = cosx.

Тогда

Интеграл вида

функция R четная относительно sinx и cosx.

Для преобразования функции R в рациональную используется подстановка

t = tgx .Тогда

Интеграл произведения синусов и косинусов

различных аргументов.

В зависимости от типа произведения применятся одна из трех формул:

30) Интегрирование рациональных дробей.

Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

Интеграл вида где n- натуральное число.

С помощью подстановки функция рационализируется.

Тогда

Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

31. Метод неопределенный коэффициентов при интегрирование рациональных дробей. Если знаменатель Q правильной рациональной дроби может быть представлена в виде

где А — коэффициент при старшей степени многочлена Q (х), α, β... — корни уравнения Q(x) = 0, а трехчлены не имеют вещест­венных корней, то эта дробь разлагается на сумму элементар­ных дробей следующим образом:

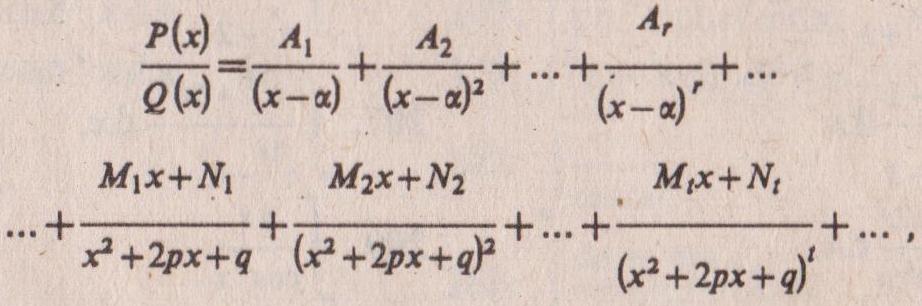(1)

где A₁, A₂, ... ,A_r, ... ,M₁, N₁, M₂, N₂, ..., M_t, N_t ... — некоторые числа, подлежащие определению. Для их определения умножают обе части последнего разложения (1) на Q (х). Так как равенство между многочленом Р(х) и многочленом, который получится в правой части, справедливо для всех х, то коэффициенты, сто­ящие при равных степенях х, равны между собой. Таким образом получим ряд уравнений первой степени, из которых найдем неиз­вестные числа A₁, А₂, ..., А_г, .... M₁, N₁ М₂, N₂, ..., М_t ,N_t ...

Изложенный метод отыскания разложения рациональной функ­ции называется методом неопределенных коэффициентов.

Если рациональная дробь неправильная, то следует предварительно выделить целую часть.