Уравнение конуса [править]

Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:

• В сферической системе координат с координатами (r, φ, θ):

• В цилиндрической системе координат с координатами (r, φ, z):

 или 

• В декартовой системе координат с координатами (x, y, z):

 Это уравнение в каноническом виде записывается как

где константы a, с определяются пропорцией   Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид

причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением   где функция   является однородной, то есть удовлетворяющей условию   для любого действительного числа α.

Свойства [править]

• Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.

• Телесный угол при вершине прямого кругового конуса равен

где   — угол раствора конуса.

• Площадь боковой поверхности такого конуса равна

• Площадь поверхности такого конуса равна

где   — радиус основания,   — длина образующей.

• Объём кругового конуса равен

• Для усечённого конуса (не обязательно прямого и кругового) объём равен:

где S₁ и S₂ — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

• Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

Уравнение конуса [править]

Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:

• В сферической системе координат с координатами (r, φ, θ):

• В цилиндрической системе координат с координатами (r, φ, z):

 или 

• В декартовой системе координат с координатами (x, y, z):

 Это уравнение в каноническом виде записывается как

где константы a, с определяются пропорцией   Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид

причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением   где функция   является однородной, то есть удовлетворяющей условию   для любого действительного числа α.

Основные геометрические формулы[править]

Площадь сферы

Объем шара, ограниченного сферой

Площадь сегмента сферы

 , где H — высота сегмента, а   — зенитный угол

Сфера в трёхмерном пространстве[править]

Уравнение

где   — координаты центра сферы,   — её радиус.

Параметрическое уравнение сферы с центром в точке  :

где   и 

Геометрия на сфере[править]

Основная статья: Сферическая геометрия

Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие окружности являютсягеодезическими линиями на сфере; любые два из них пересекаются в двух точках.

Расстояние между двумя точками на сфере[править]

Если даны сферические координаты двух точек, то расстояние между ними можно найти так:

Однако, если угол   задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:

В этом случае   и   называются широтами, а   и   долготами.

Число сочетаний [править]

Основная статья: Биномиальный коэффициент

Число сочетаний из   по   равно биномиальному коэффициенту

При фиксированном   производящей функцией последовательности чисел сочетаний  ,  ,  , … является:

Двумерной производящей функцией чисел сочетаний является

Сочетания с повторениями [править]

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Число сочетаний с повторениями из   по   равно биномиальному коэффициенту

Доказательство.

Пусть имеется   типов объектов, причём объекты одного типа неотличимы. Пусть имеется неограниченное (или достаточно большое, во всяком случае, не меньше  ) количество объектов каждого типа. Из этого ассортимента выберем   объектов; в выборке могут встречаться объекты одного типа, порядок выбора не имеет значения. Обозначим через  количество выбранных объектов  -го типа,  ,  . Тогда  . Но число решений этого уравнения легко подсчитывается с помощью «шаров и перегородок»: каждое решение соответствует расстановке в ряд   шаров и   перегородок так, чтобы между  -й и  -й перегородками находилось ровно  шаров. Но таких расстановок в точности  , что и требовалось доказать.

При фиксированном   производящей функцией чисел сочетаний с повторениями из   по   является:

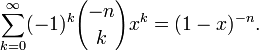
Двумерной производящей функцией чисел сочетаний с повторениями является: