Определение[править]

Пусть   определена на  . Разобьём  на части с несколькими произвольными точками  . Тогда говорят, что произведено разбиение  отрезка   Далее выберем произвольную точку  ,  ,

Определённым интегралом от функции   на отрезке  называется предел интегральных сумм при стремлении ранга разбиения к нулю  , если он существует независимо от разбиения   и выбора точек  , то есть

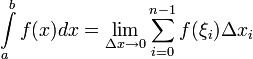
Если существует указанный предел, то функция   называется интегрируемой на   по Риману.

Обозначения[править]

•  — нижний предел.

•  — верхний предел.

•  — подынтегральная функция.

•  — длина частичного отрезка.

•  — интегральная сумма от функции   на   соответствующей разбиению  .

•  — максимальная длина част. отрезка.

Свойства[править]

Если функция   интегрируема по Риману на  , то она ограничена на нем.

Геометрический смысл[править]

Определённый интеграл как площадь фигуры

Определённый интеграл   численно равен площади фигуры, ограниченной осью абсцисс, прямыми   и   и графиком функции  .

Формула ньютона- лейбница

Если   непрерывна на отрезке   и   — её любая первообразная на этом отрезке, то имеет место равенство

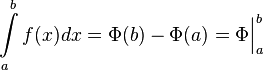
Сложение векторов с использованием координат. Каждая координата (см. Базис и разложение по базису) суммы векторов есть сумма соответствующей координаты всех (двух или более) суммируемых векторов. Например, для двумерного случая:

Операция вычитания из вектора   вектора   сводится к сложению первого вектора и вектора, противоположного второму:

Векторное произведение[править]

Основная статья: Векторное произведение

Векторным произведением вектора   на вектор   называется вектор  , удовлетворяющий следующим требованиям:

• длина вектора   равна произведению длин векторов   и   на синус угла φ между ними

• вектор   ортогонален каждому из векторов   и 

• вектор   направлен так, что тройка векторов   является правой.

Обозначение: 

Геометрически векторное произведение   есть ориентированная площадь параллелограмма, построенного на векторах  , представленная псевдовектором, ортогональным этому параллелограмму.

Свойства векторного произведения:

1. При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е 

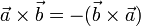
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть 

3. Векторное произведение обладает распределительным свойством: 

Свойства призмы[править]

• Основания призмы являются равными многоугольниками.

• Боковые грани призмы являются параллелограммами.

• Боковые ребра призмы параллельны и равны.

• Объём призмы равен произведению её высоты на площадь основания:

• Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

• Площадь боковой поверхности произвольной призмы 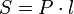 , где   — периметр перпендикулярного сечения, 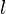  — длина бокового ребра.

• Площадь боковой поверхности правильной призмы  , где   — периметр основания призмы,   — высота призмы.

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.

• Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.

• Перпендикулярное сечение перпендикулярно ко всем боковым граням.