Действия над комплексными числами

• Сравнение

 означает, что   и   (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

• Сложение

• Вычитание

• Умножение

• Деление

Тригонометрическая форма

Если вещественную   и мнимую   части комплексного числа выразить через модуль   и аргумент   ( ,  ), то всякое комплексное число  , кроме нуля, можно записать в тригонометрической форме

Показательная форма

Применяя формулу Эйлера к тригонометрической форме, получим показательную форму комплексного числа:

где   — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

Свойство умножения: Произведение двух комплексных чисел z1=r1 cos 1+isin 1   и z2=r2 cos 2+isin 2   будет комплексное число вида z1 z2=r1 r2 cos( 1+ 2)+isin( 1+ 2)  

Свойство деления: Частное двух комплексных чисел z1=r1 cos 1+isin 1   и z2=r2 cos 2+isin 2  будет комплексное число вида z2z1=r2r1 cos( 1− 2)+isin( 1− 2)  

Свойство возведение в степень: Степень комплексного числа z=r cos +isin   будет комплексное число вида  r cos +isin n=rn cosn +isinn  

Свойство извлечения корня: Корень из комплексного числа z=r cos +isin   будет комплексное число вида  nr cos +isin = nr cosn +2 k+isinn +2 k k=0;1;2; ;n−1 

Формула Муавра :  cos +isin n=cosn +isinn  

Действия с корнями.Степень с рациональным и действительным показателем

5. Действия с корнями (радикалами).

а) Арифметический корень   -й степени из числи   (обозначается     ) - неотрицательное число,   -я степень которого равна  , т. е. если   то

  

Если   то арифметический корень из числа   обозначается   и называется арифметическим квадратным корнем.

б) Свойства арифметического корня    

      

          

    

    

в) Для любого   справедливо равенство

  

и, в частности,

  

г) Если   то

.

д) Формула «сложного радикала». Если   то

  

6. Степень с рациональным и действительным показателем.

а) Степень с рациональным показателем определяется равенством

 где    

б) Свойства степени с рациональным показателем (   - рациональные числа,     ).

 

      

 

в) Степень с действительном иррациональным показателем   и основанием  , где   определяется как действительное число (обозначается   ), являющееся пределом последовательности   где   - последовательность рациональных чисел такая, что   . При этом для степени с любым действительным показателем справедливы те же свойства, которыми обладает степень с рациональным показателем. Это доказывается в курсе высшей математики.

Логари́фм числа   по основанию   (от греч. λόγος — «слово», «отношение» и ἀριθμός — «число»^[1]) определяется^[2] как показатель степени, в которую надо возвести основание  , чтобы получить число  . Обозначение:  , произносится: "логарифм   по основанию ".

Из определения следует, что нахождение   равносильно решению уравнения  . Например,   потому что 

Основное логарифмическое тождество

Из определения логарифма следует основное логарифмическое тождество^[7]:

Следствие: из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений. В самом деле, если  , то  , откуда, согласно основному тождеству: 

Замена основания логарифма

Логарифм   по основанию   можно преобразовать в логарифм по другому основанию  ^[5]:

Следствие (при   ) — перестановка основания и логарифмируемого выражения:

Другие тождества и свойства

Если выражения для основания логарифма и для логарифмируемого выражения содержат возведение в степень, для упрощения можно применить следующее тождество:

Это тождество сразу получается, если в логарифме слева заменить основание   на   по вышеприведенной формуле замены основания. Следствия:

Ещё одно полезное тождество:

Для его доказательства заметим, что логарифмы левой и правой частей по основанию   совпадают (равны  ), а тогда, согласно следствию из основного логарифмического тождества, левая и правая части тождественно равны.

	Формула	Пример
Произведение
Частное от деления
Степень
Корень

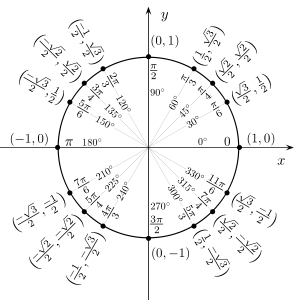
Значения тригонометрических функций для некоторых углов [править]

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).

	0°(0 рад)	30° (π/6)	45° (π/4)	60° (π/3)	90° (π/2)	180° (π)	270° (3π/2)	360° (2π)