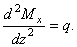- •1.Кручение: общая картина деформации: скручивающие и крутящие моменты, эпюра крутящих моментов
- •2.Вывод формулы для определения касат напряжений при кручении стержней круглого поперечного сечения
- •3.Кручение: деформация бруса круглого поперечного сечения; жесткость при кручении; эпюра углов закручивания.
- •4.Нагружения на наклонных площадках при кручении. Характер разрушения материалов.
- •5.Кручение: главные напряжения, расчеты на прочность и жесткость, условие прочности.
- •6. Кручение бруса некруглого поперечного сечения: напряжения, деформации, геометрические характеристики; эпюра касательных напряжений для бруса прямоугольного поперчечного сечения
- •7.Кручение тонкостенного бруса замкнутого и открытого профилей.
- •8.Потенциальная энергия при кручении.
- •9. Статически неопределимые задачи при расчете на кручение
- •10. Плоский поперечный изгиб. Внутренние силы. Напряжения.
- •11.Характер поведения материалов при чистом изгибе. Гипотезы Бернулли.
- •13.Напряжения в наклонной площадке. Главные напряжения при изгибе и их эпюры.
- •16.Методика расчетов на прочность по нормальным напряжениям при изгибе прямых брусьев
- •17. Центр изгиба: понятие и экстремальное определение.
- •18.Понятие о прогибе и угле поворота. Вывод приближенного дифференциального уравнения изогнутой оси.
- •19. Нормальные напряжения при чистом изгибе (вывод формулы, эпюра, энергия упругой деформации.)
- •20.Касательные напряжения при поперечном изгибе(вывод формулы Журавского, эпюра).
- •21.Проверка прочности по касательным и нормальным напряжениям при изгибе.
- •22.Расчет балок на прочность. Балки равного сопротивления изгибу.
- •23.Перемещения сечений при изгибе. Метод начальных параметров.
- •24. Расчет балок на жесткость. Потенциальная энергия деформации.
- •25.Балки разнородной упругости.
- •26.Статически неопределимые балки. Методика раскрытия статической неопределимости.
- •27.Косой изгиб: общие положения, напряжения и положение нейтр лин.
- •28. Определение прогибов при косом изгибе. Понятие об осях большой и малой жёсткости.
- •29.Сложное сопротивление. Совместное действие изгибающих моментов и продольной силы.
- •30.Понятие о внецентренном растяжение и сжатие: общие положения, внутренние силы, напряжения, положение нулевой линии, ядро сечения.
- •31.Вывод формул для определения нормальных напряжений при внецентренном растяжении и сжатии и положения нейтральной линии
- •32.Ядро сечения. Методика построения.
- •33. Одновременное действие кручение и изгиба; кручение с растяжением или сжатием. Расчет по эквивалентным напряжениям.
- •34.Совместное действие крутящих, изгибающих моментов и продольной силы в случае стержней с некруглым поперечным сечением.
- •35.Совместное действие крутящих, изгибающих моментов и продольной силы в случае стержней с круглым поперечным сечением.
- •36.Кривые стержни:основные положения;вычисление изгиб мом, норм и попереч сил; вычисление напряжений; определение положения нейтр слоя.
- •37.Устойчивость сжатых стержней: общие положения, понятие о критической силе, формула эйлера и пределы ее применимости.
- •38.Устойчивость сжатых стержней: гибкость стержня, предельная гибкость, формула Ясинского, расчеты на устойчивость.
- •40.Толстостенные трубы: основные уравнения для осесимметричного тела.
- •41.Толстостенные трубы: расчёт цилиндра нагруженного внутренним давлением, расчёт цилиндра нагруженного внешним давлением, эпюра напряжений.
- •42.Толсостенные трубы: определение перемещений и напряжений.
- •43.Основы расчёта на действие динамических нагрузок: общие положения, приближенный способ расчёта на удар.
- •44. Основы расчёта на действие динамических нагрузок: общие положения, расчет троса при подъеме груза.
- •45.Циклические нагрузки. Усталость материала. Природа усталости материала.
- •46. Прочность при циклических нагрузках: расчёт на усталустную прочность цилиндрической клапанной пружины.
- •47. Прочность при циклич нагрузках: диаграмма усталост прочности, влияние концентрации напряжений, состояния поверхности и размеров детали на усталостную прочность.
- •49 Расчет тонкостенных сосудов
10. Плоский поперечный изгиб. Внутренние силы. Напряжения.
Изгибом называется деформация, сопровождающаяся изменением кривизны оси стержня. Напряженно-деформированное состояние изгиба стержня вызывается парами сил, расположенными в продольных плоскостях стержня. Стержень, работающий на изгиб, называется балкой. Если нагрузка прикладывается в плоскости симметрии, то ось изогнутой балки представляет собой плоскую кривую, расположенную в плоскости действия нагрузки. Такой случай изгиба называется плоским изгибом. Изгиб происходит от сил, расположенных перпендикулярно оси балки; поэтому он называется поперечным.
При плоском поперечном изгибе в балке возникают два вида внутренних усилия: поперечная сила Q и изгибающий момент M. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.
Если
изгибающий момент
![]() является единственным внутренним
силовым фактором, то такой изгиб
называется чистым.
При
наличии поперечной силы
является единственным внутренним
силовым фактором, то такой изгиб
называется чистым.
При
наличии поперечной силы
![]() изгиб
называется поперечным.
Строго говоря, к простым видам сопротивления
относится лишь чистый изгиб; поперечный
изгиб относят к простым видам сопротивления
условно, так как в большинстве случаев
(для достаточно длинных балок) действием
поперечной силы при расчетах на прочность
можно пренебречь
изгиб
называется поперечным.
Строго говоря, к простым видам сопротивления
относится лишь чистый изгиб; поперечный
изгиб относят к простым видам сопротивления
условно, так как в большинстве случаев
(для достаточно длинных балок) действием
поперечной силы при расчетах на прочность
можно пренебречь
11.Характер поведения материалов при чистом изгибе. Гипотезы Бернулли.
При прямом чистом изгибе в поперечном сечении стержня возникает только один силовой фактор — изгибающий момент Мх (рис. 1). Так как Qy=dMx/dz=0, то Mx=const и чистый прямой изгиб может быть реализован при загружении стержня парами сил, приложенными в торцевых сечениях стержня. Поскольку изгибающий момент Mх по определению равен сумме моментов внутренних сил относительно оси Ох с нормальными напряжениями его связывает выкающее из этого определения уравнение статики
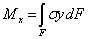 .
.
1.)Гипотеза плоских сечений была установлена Я. Бернулли в результате экспериментов: при растяжении стержня продольные и поперечные риски, нанесенные на его поверхности до деформации, остаются прямолинейными и взаимно перпендикулярными, изменяются лишь расстояния между ними (между поперечными рисками они увеличиваются, а между продольными – уменьшаются).
В основе гипотезы плоских сечений лежит предположение, что и внутри стержня деформации имеют такой же характер, как на поверхности. Следовательно, сечения, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации. В этом и заключается смысл гипотезы плоских сечений.
2) гипотеза о постоянстве нормальных напряжений - напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса; 3) гипотеза об отсутствии боковых давлений - соседние продольные волокна не давят друг на друга.
1 2.Изгиб
прямого бруса: основные положения;
опоры; внутренние силовые факторы и
правила знаков; основные дифференциальные
соотношения теории изгиба.
2.Изгиб
прямого бруса: основные положения;
опоры; внутренние силовые факторы и
правила знаков; основные дифференциальные
соотношения теории изгиба.
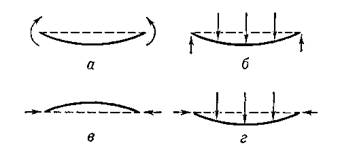 а
чистый: б поперечный; в продольный; г
прод-поперечный.
Брус,
работающий на изгиб, называется балкой.
Изгиб называется плоским, если ось балки
после деформации остается плоской
линией. ()
расположения изогнутой оси балки назыв
()
изгиба. ()
действия нагрузочных сил называется
силовой плоскостью. Если силовая
плоскость совпадает с одной из главных
плоскостей инерции поперечного сечения,
изгиб называется прямым. (В противном
случае косой изгиб). Главная ()
инерции поп сеч - это (),
образ.
одной из главных осей поперечного
сечения с продольной осью бруса. При
плоском прямом изгибе ()
изгиба и силовая ()
совпадают.
В
отличие от консольных балок, при расчете
балок на двух шарнирных опорах необходимо
сначала определить опорные реакции из
уравнений статики, так как и в левую, и
в правую отсеченные части для любого
сечения, расположенного между опорами,
попадает соответствующая реакция.
Выделить
еще
2
подхода к построению эпюр. В 1
случае намечают не характерные сечения,
а характерные точки, в качестве которых
выделяют точки приложения сосредоточенных
сил и моментов, а также точки начала и
конца участков с распределенными
нагрузками. Затем определяют величину
внутреннего силового фактора слева и
справа от характерной т.
2
--
балка разбивается на участки. Для каждого
участка записывается выражение
внутреннего силового фактора в общем
виде как функции координаты z
.
Затем вычисляются значения на концах
каждого участка.
Очевидно,
что при обоих подходах в конечном счете
все сводится к вычислению внутренних
силовых факторов в
характерных сечениях,
то есть соответствует описанному выше
способу, но требует дополнительной, как
правило неоправданной, работы.
Правда,
следует отметить, что запись общих
выражений как функций от
а
чистый: б поперечный; в продольный; г
прод-поперечный.
Брус,
работающий на изгиб, называется балкой.
Изгиб называется плоским, если ось балки
после деформации остается плоской
линией. ()
расположения изогнутой оси балки назыв
()
изгиба. ()
действия нагрузочных сил называется
силовой плоскостью. Если силовая
плоскость совпадает с одной из главных
плоскостей инерции поперечного сечения,
изгиб называется прямым. (В противном
случае косой изгиб). Главная ()
инерции поп сеч - это (),
образ.
одной из главных осей поперечного
сечения с продольной осью бруса. При
плоском прямом изгибе ()
изгиба и силовая ()
совпадают.
В
отличие от консольных балок, при расчете
балок на двух шарнирных опорах необходимо
сначала определить опорные реакции из
уравнений статики, так как и в левую, и
в правую отсеченные части для любого
сечения, расположенного между опорами,
попадает соответствующая реакция.
Выделить
еще
2
подхода к построению эпюр. В 1
случае намечают не характерные сечения,
а характерные точки, в качестве которых
выделяют точки приложения сосредоточенных
сил и моментов, а также точки начала и
конца участков с распределенными
нагрузками. Затем определяют величину
внутреннего силового фактора слева и
справа от характерной т.
2
--
балка разбивается на участки. Для каждого
участка записывается выражение
внутреннего силового фактора в общем
виде как функции координаты z
.
Затем вычисляются значения на концах
каждого участка.
Очевидно,
что при обоих подходах в конечном счете
все сводится к вычислению внутренних
силовых факторов в
характерных сечениях,
то есть соответствует описанному выше
способу, но требует дополнительной, как
правило неоправданной, работы.
Правда,
следует отметить, что запись общих
выражений как функций от
![]() удобна
при программировании построения эпюр
при помощи вычислительной техники.Правило
знаков:
-для
Q
для
М
удобна
при программировании построения эпюр
при помощи вычислительной техники.Правило
знаков:
-для
Q
для
М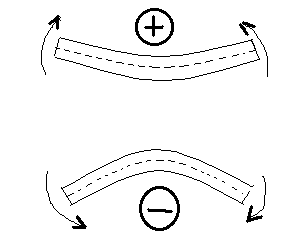
при
вычислении:
В поперечном сечении
разреза мысленно представим заделку:
внешняя сила (момент) изгибающая балку
выпуклостью вниз (сжимающая верхние
волокна) дает положительный внутренний
момент.
Пусть
брус нагружен произвольным образом
распределенной нагрузкой
![]() (рис. а).
(рис. а).

Выделим
из бруса элемент длиной
![]() и
приложим по его краям положит внутр
усилия (рис.
б).
В пределах малого отрезка
нагрузку
и
приложим по его краям положит внутр
усилия (рис.
б).
В пределах малого отрезка
нагрузку
![]() можно считать распределенной равномерно.
Приравняем нулю сумму проекций всех
сил на вертик ось y и сумму мом всех F
относительно поперечной оси x,
проходящей через точку С
(рис. б),
получим:
можно считать распределенной равномерно.
Приравняем нулю сумму проекций всех
сил на вертик ось y и сумму мом всех F
относительно поперечной оси x,
проходящей через точку С
(рис. б),
получим:
![]() ;
;
![]() .
.
Производя
упрощения и отбрасывая величины высшего
порядка малости, получим теорему
Журавского (теорему Шведлера):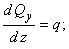
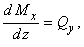 откуда
откуда