8.Потенциальная энергия при кручении.

Потенциальная энергия деформации при кручении определяется подобно тому, как это делалось при растяжении и сдвиге.Удельная потенциальная энергия деформации при чистом сдвиге определяется из уравнении:

.

Потенциальная энергия деформации U определится из уравнения путем интегрирования по объему:

.

При этом учитывалось, что 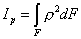. В брусе постоянной жесткости GI_p при действии постоянного по длине крутящего момента, имеем

.

9. Статически неопределимые задачи при расчете на кручение

Системы, в которых количество наложенных связей больше, числа независимых уравн равновесия,называются стат неопред.По сравнению со стат определимыми системами, в ста неопрд. системах имеются дополнительные лишние связи.Термин “лишние связи” является условным. Эти связи являют­ся лишними с точки зрения расчетных предпосылок. В действи­тельности эти связи создают дополнит резервы для конст­рукций, как в плане обеспечения её жесткости, так и прочности.На рис. 2.5, а изображен кронштейн, сост из 2 стерж­ней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертик усилие Р, а система яв­ляется плоской получается, что усилия в стержнях легко определ. из условий равновесия узла А, т.е.x = 0, y = 0. Раскрывая эти уравнения, получаем замкнутую систему лин уравнений относительно неизвестных усилий N₁ и N₂ в кото­рой количество уравнений равно количеству неизвестных:N₁  N₂ sin  = 0;N₂ cos   Р = 0.

Если конструкцию крон­штейна усложнить, добавив еще один стержень (рис. 2.5, б), то усилия в стержнях N₁, N₂ и N₃ прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.16) имеются 3 неиз­вестных усилия в стержнях. Получ сис­тема один раз ста неопределима. Разность между числом неизвестных усилий и количеством независимых (значащих) урав­нений равновесия, связывающих эти усилия, называется сте­пенью ст неопредел рассматриваемой системы.В общем случае под nраз статически неопределимой системой понимается система, в которой число неизвестных внешних опорных реакций и внутренних усилий превышает число не­зависимых и значащих уравнений равновесия на n единиц. Решение статически неопределимых задач методом сил проводится в такой последовательности.1Устанавливае степень ст неопред системы как разность между числом искомых неизв усилий и числом независ уравн равновесия. Учитывается, что простой шарнир, соединяющ 2 стержня системы, уменьшает степень ст неопределим на 1, т к снимает одну связь, препятств повороту одной части системы относительно другой. Простой шарнир позволяет добавить к уравн. равн. всей системы уравнение равновесия присоединенной этим шарниром части системы.2. Из заданной ст неопр. сист выделяется основная система путем удаления лишних связей и внешней нагрузки.3. Изображается соответствующая выбранной основной эквивалентная система, в которой взамен снятых лишних связей и в их направлении приложены силы X_i, если связи препятствовали линейному перемещению, и пары X_k, если они исключали повороты сечений.4. Составляются канонические уравнения метода сил.5. Вычисляются коэффициенты канонических уравнений аналитически
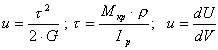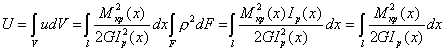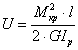