46. Прочность при циклических нагрузках: расчёт на усталустную прочность цилиндрической клапанной пружины.

1. Определяем макси­мального max и мини­мального min напря­жений в проволоке пружины и вычисле­ние коэффициент асимметрии цикла R. Для вычисления напря­жений используем фор­мулу:

где k  коэфф., учитыва­ющий поперечную силу и неравномерность рас­пределения напряжений от ее воздействия, а также влияние дефор­мации изгиба вследствие кривизны витков пружины. Этот коэффициент можно определить по приближенной фор­муле: ,

Коэффициент асимметрии цикла:

.

2. Найдем среднего m и амплитудного a напря­жений цикла. Найдем величину среднего и амплитудного напря­жений цикла в зависимости от max и min:

кН/м2,

кН/м2.

3. Определение коэффициента запаса прочности. Де­таль (пружина) может перейти в предельное состояние по уста­лости и по причине развития пластических деформаций. Коэф­фициент запаса прочности по усталости определяются по форму­лам (9.10):

,

где 1  предел выносливости при симметричном цикле.

.

Если < ,то то коэффициент запаса выбирается по пределу текучести.

Если < ,то коэффициент запаса прочности для пру­жины определяется усталостью

47. Прочность при циклич нагрузках: диаграмма усталост прочности, влияние концентрации напряжений, состояния поверхности и размеров детали на усталостную прочность.

Многие детали машин и механизмов, а также конструкции со­оружений в процессе эксплуатации подвергаются циклически изме­няющимся во времени воздействиям. Если уровень напряжений, вызванный этими воздействиями, превышает определенный пре­дел, то в материале формируются необратимые процессы накопле­ния повреждений, которые в конечном итоге приводят к разруше­нию системы.

Процесс постепенного накопления повреждений в материале под действием переменных напряжений, приводящих к разруше­нию, называется усталостью. Свойство материала противо­стоять усталости называется выносливостью. На величину предела усталости влия­ют многие факторы. Рассмотрим некото­рые из них.

Одним из основных факторов, оказывающих существенное влияние на усталостную прочность, является кон­центрация напряжений. Основным пока­зателем местных напряжений является коэффициент концентрации напряже­ний:

, где max  наибольшее местное напряже­ние, НОМ  номинальное напряжение. При расчетах на усталостную прочность, особенности, связан­ные с качеством обработки поверхности детали, учитываются коэф­фициентом качества поверхности, получаемом при симметричных циклах нагружения:

,

Для учета масштабного фактора вводятся соответствующий коэффициент:

.

Диаграмма усталостной прочности:

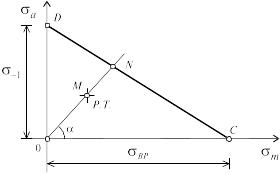
48. Витые пружины. Цилиндрические пружины растяжения и сжатия. Основное применение в машиностроении имеют пружины из круглой проволоки благодаря их наименьшей стоимости и лучшей их работой при напряжениях кручения. Пружины характеризуются следующими основными геометрическими параметрами: диаметр проволоки d; средний диаметр D; индекс пружины c = D/d; шаг витков h; угол подъема витков , ;длина рабочей части пружины Н_Р;число рабочих витков i = H_P/h. Чем податливее должна быть пружина, тем больше берется индекс пружины и число витков. Пружины растяжения навивают таким образом, чтобы было обеспечено начальное натяжение между витками. Это натяжение выбирают 1/3…1/4 предельной силы для пружины, при которой ее испытывают и которая вызывает напряжения, близкое к пределу упругости. Такую навивку называют закрытой. На концах пружин для крепления могут быть прицепы в виде изогнутых витков. Наиболее совершенными являются крепления с помощью ввертываемых резьбовых пробок с крючками. Пружины сжатия навивают открытой навивкой с просветом между витками на 10…20% больше расчетных осевых упругих перемещений каждого витка при максимальных рабочих нагрузках. Для того чтобы нагрузка на пружину передавалась по ее оси, конечные витки прижимают к соседним виткам, а торцевые поверхности пружины шлифуют. Силовые факторы, действующие в лобовом поперечном сечении пружин растяжения и сжатия, сводятся к моменту M = FD/2, вектор которого перпендикулярен оси пружины и силе F, действующей вдоль оси пружины. Момент М раскладывается на крутящий Т и изгибающий М_И моменты и (1)

В большинстве пружин угол подъема витков небольшой, не превышает  10…12^о. Поэтому расчет можно вести по крутящему моменту, пренебрегая изгибающим моментом из-за его малости. Максимальное напряжение кручения, возникающее на внутренних волокнах, составляет

(2) где k – коэф, учитывающий кривизну витков, .

c = D/d …………..4……..5……6…..…8….…10…12 k..1,37.1,29.1,24…1,17…..1,14….1,11

Из приведенной зависимости (2) получаем формулу для определения диаметра проволоки при проектном расчете пружин . (3)

Осевое упругое сжатие пружин определяют как суммарный угол закручивания пружины , умноженный на средний радиус пружины

, (4) где ₁ – податливость одного витка, то есть сжатие витка от единичной силы, ; G – модуль сдвига.

Потребное число рабочих витков определяют по условию, по которому при возрастании нагрузки от установочной (начальной) F_min до максимальной F_max пружина должна получить заданное упругое перемещение

. (5)

Откуда вычисляют число витков

. (6)

Полная длина ненагруженной пружины составляет

, (7)где Н₃ – длина пружины, сжатой до соприкосновения соседних рабочих витков, , полное число витков уменьшено на 0,5 из-за шлифовки каждого конца пружины на 0,25d для образования плоского опорного торца. i₁ – полное число витков, , дополнительные 1,5…2,0 витка идут на поджатие для создания опорных поверхностей пружин.

Максимальная осадка пружины, т. е. перемещение торца пружины до полного соприкосновения витков составляет,

. (8)

Шаг пружины определяется по зависимости

. (9)

Длину проволоки для изготовления пружины рассчитывают из соотношения

. (10)