40.Толстостенные трубы: основные уравнения для осесимметричного тела.

Если толщина стенки трубы, нагруженной радиальной на­грузкой, превышает 0,1 радиуса геометрической оси стенки, труба считается толстостенной. Труба нагружена на внутренней и наружной поверхностях радиальной сжимающей нагрузкой; интенсивности р_В и р_Н этой нагрузки по­стоянны как вдоль оси трубы, так и по ее окружности.  Составим уравнение равновесия элемента трубы, выделенного двумя радиальными сечениями, составляющими между собой угол , и двумя окружными сечениями, радиусы которых r и r + dr. По граням этого элемента действуют радиаль­ные и окружные напряжения и . Радиальное напряжение при изменении радиуса r получает приращение 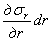, а окружное напряжение в силу осевой симметрии задачи при изменении угла не меняется. Диф уравнение равновесия для осесимметричной задачи имеет вид:

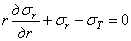. (3.1)

Напря­жения и выразим через относительные линейные деформа­ции с помощью закона Гука:

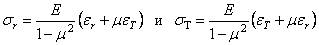, (3.2)

а относительные деформации заменим их выраже­ниями через радиальное перемещение v (рис. 30,б), пользуясь зависимостями

.

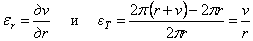Подставив эти выражения в формулу (3.2), а выражения (3.2) в фор­мулу (3.1), получим выражения для напряжений и дифферен­циальное уравнение равновесия элемента трубы в перемещениях

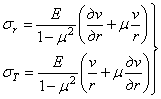(3.3)

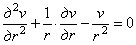(3.4)

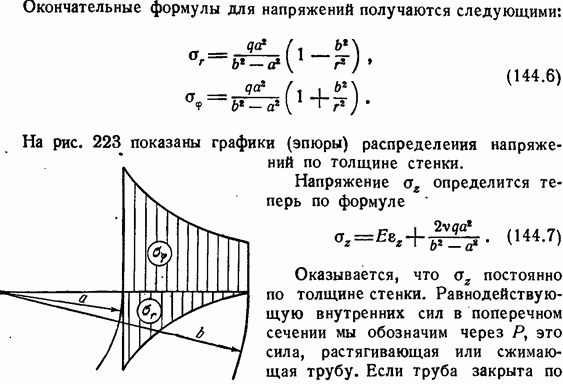
41.Толстостенные трубы: расчёт цилиндра нагруженного внутренним давлением, расчёт цилиндра нагруженного внешним давлением, эпюра напряжений.

Цилиндр высокого давления мультипликатора является одним из ответственных элементов гидроразрезного станка. В материале любого по конструкции цилиндра под действием нагрузки возникают напряжения, под влиянием котор он испытывает деформацию. Расчет цилиндров, работающих под большим давлением, заключается в основном в определении толщины стенок, при которой цилиндр мог бы выдержать приложенную нагрузку без остаточных деформаций. Для цилиндров, работающих при очень высоких давлениях (более 50 МПа), при расчете толщины стенок необходимо учитывать также пластические деформации цилиндра, появление которых от действия внутреннего давления используют, как это будет показано далее, при конструировании цилиндров. В толстостенном цилиндре под действием внутреннего давления развиваются три основных напряжения — радиальные, тангенциальные, осевые. Однако величины первых двух не будут постоянными по всей толщине стенки, а будут изменяться гиперболически. Рассмотренные три основные напряжения, перпендикулярные друг к другу, создают сложные условия напряжений в стенке цилиндра, что определяет приближенность математических расчетов, так как вопрос о моменте перехода упругих деформаций в пластические при сложном напряженном состоянии материала до сих пор окончательно не решен. Приближенно задачу решают с помощью теорий прочности, заменяя данное сложное напряженное состояние эквивалентным ему состоянием растяжения.

42.Толсостенные трубы: определение перемещений и напряжений.

Если толщина стенки трубы, нагруж радиальной на­грузкой, превышает 0,1 R геометр оси стенки, труба считается толстостенн. Распределение напряж по толщине стенки такой трубы нельзя считать равномерным; радиальные пере­мещ отдельных точек стенки трубы зависят от их расстоя­ния r до оси трубы. С помощью теории расчета толстостенных труб определяются напряжения и перемещения в точках стенок цилиндров машин, стволов орудий, при температурных или прессовых посадках рубашек, муфт и ступиц на валы, а также в облицовках тоннелей и стволов, подверженных горному давлению. Рассмотрим отрезок трубы длиной, равной единице, вырезанный двумя сечениями, нормальными к оси трубы (рис. 30,а). Труба нагружена на внутренней и наружной поверхностях радиальной сжимающей нагрузкой; интенсивности р_В и р_Н этой нагрузки по­стоянны как вдоль оси трубы, так и по ее окружности. Любой такой отрезок на некотором расстоянии от торцов трубы находится в плоском деформированном состоянии.  Составим уравнение равновесия элемента трубы, выделенного двумя радиальными сечениями, составляющими между собой угол , и двумя окружными сечениями, радиусы которых r и r + dr (рис. 30,б). По граням этого элемента действуют радиаль­ные и окружные напряжения и . Радиальное напряжение при изменении радиуса r получает приращение , а окружное напряжение в силу осевой симметрии задачи при изменении угла не меняется. Дифференциальное уравнение равновесия (1.32,б) для осесимметричной задачи имеет вид (3.1)

Напря­жения и выразим через относительные линейные деформа­ции с помощью закона Гука: (3.2)

а относит деформации заменим их выраже­ниями через радиальное перемещение v (рис. 30,б), пользуясь зависимостям .

Подставив эти выражения в формулу (3.2), а выражения (3.2) в фор­мулу (3.1), получим выражения для напряжений и дифферен­циальное уравнение равновесия элемента трубы в перемещениях

(3.3)

(3.4)