27.Косой изгиб: общие положения, напряжения и положение нейтр лин.

 Косой изгиб - изгиб, при котором () изгиб момента не совпадает ни с одной из главных осей поперечного сечения (рис. 5.27, а). Косой изгиб удобнее всего рассмотреть как одновременный изгиб бруса относи­тельно главных осей x и y поперечного сечения бруса. Для этого общий вектор изгибающего момента М, действующего в попереч­ном сечении бруса, раскладывается на составляющие момента от­носит этих осей (5.27, б): M_x = M×sina;     M_y = M×cosa .       (5.25)

Введем следующее правило знаков для моментов M_x и M_y - момент считается положительным, если в первой четверти коорди­натной плоскости он вызывает сжимающие напряжения.

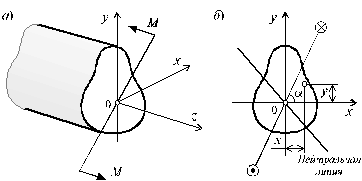Рис. 5.27

      На основании принципа независимости действия сил нормаль­ное напряжение в произвольной точке, принадлежащей к попереч­ному сечению бруса и имеющей координаты x, y, определяется суммой напряжений, обусловленных моментами M_x и M_y , т.е. .           (5.26)

      Подставляя выражения M_x и M_y  из (5.25) в (5.26), получим: .

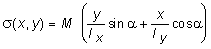      Из курса аналитической геометрии известно, что последнее вы­ражение представляет собой уравнение плоскости. Следовательно, если в каждой точке сечения отложить по нормали вектор напря­жения s, то концы векторов образуют геометрическое место точек, принадлежащих одной плоскости, как и при поперечном изгибе. Уравнение нейтральной линии, т.е. геометрического места точек, где нормальное напряжение принимает нулевые значения, найдем, полагая в (5.26) s = 0: .

      Откуда определяется: .                     (5.27)

      Поскольку свободный член в (5.27) =0 нейтральная линия всегда проходит через начало координат. Эпюра напряжений в поп сечениях бруса линейна, следовательно, мах напряжения в сечении воз­никают в точках наиболее удаленных от нейтральной линии. В том случае, когда сечение имеет простую форму (прямоугольник, круг), положение наиболее опасных точек легко определяется визуально. Для сечений, имеющих сложную форму, необходимо применить графический подход. Далее покажем, что при косом изгибе нейтральная линия не перпендикулярна к плоскости действия изгибающего момента, как это всегда выполнялось при поперечном изгибе. Действительно угловой коэффициент K₁ следа момента (рис. 5.27, б) равен:

K₁ = tg a .                                              (5.28)

      Угловой коэффициент нейтр линии определяется выражением:

tg j  = K₂  .                         (5.29)

            Так как в общем случае I_x ¹ I_y, то условие перпендикулярности прямых, известное из аналитической геометрии, не соблюдается, поскольку K₁ ¹  . Брус, образно выражаясь, предпочитает изги­баться не в плоскости изгибающего момента, а в некоторой другой плоскости, где жесткость на изгиб будет минимальной.

28. Определение прогибов при косом изгибе. Понятие об осях большой и малой жёсткости.

При нагружении 2 стержней на изгиб ос с большей жесткостью будет у того стержня. Который прогнется меньше.

29.Сложное сопротивление. Совместное действие изгибающих моментов и продольной силы.

Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.

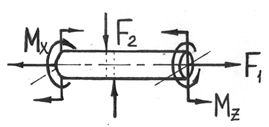
Сложный вид деформации можно рассматривать как сумму простых видов(растяжение, изгиб, кручение), при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор (рис.7.2): нормальная сила N - при растяжении, изгибающий момент М_z - при чистом изгибе, крутящий момент М_x - при кручении. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми.

   

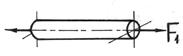
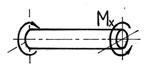
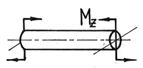
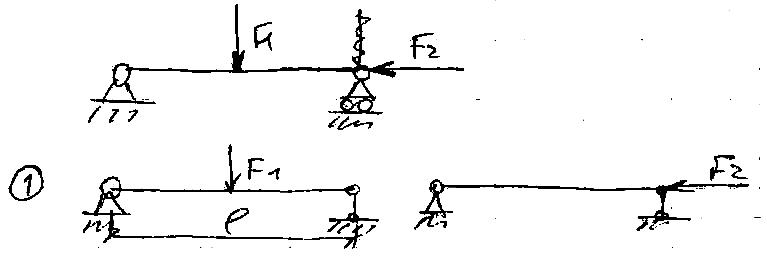
Используя метод суперпозиции, рассматриваем все виды нагружений в отдельности по соответствующим эпюрам:

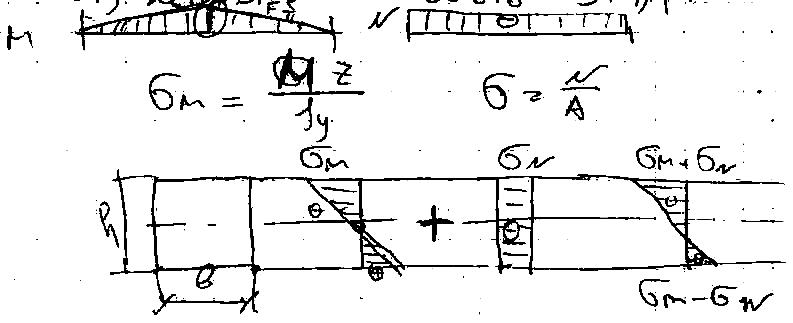
При совместном действии изгиба и продольной силы условие прочности имеет вид: 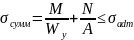. Из условий прочности определить размеры поперечных сечений при проектном расчёте не представляется возможным, так как искомые величины в разных степенях. Так как при совместном действии из условий прочности размеры поперечных сечений определить не представляется возможным, то в случае проектных расчётов используем метод последовательных приближений. Первоначальные размеры поперечных сечений определяем по методике плоского поперечного изгиба и выполняем проверочный расчёт с учётом продольной силы, если условие прочности не будет выполняться, увеличиваем размеры поперечного сечения и повторяем расчёты на проверку прочности, учитывая, что перенапряжение или недонапряжение, если нет ограничений в технических условиях, не должны превышать 5%.