1.Кручение: общая картина деформации: скручивающие и крутящие моменты, эпюра крутящих моментов

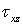К ручением называется такой вид деформ, при котором в поп сеч стержня возникает лишь один силовой фактор — крутящий мом М_z. Крутящий мом по опред равен сумме моментов внутренних сил относительно продольной оси стержня Oz. Норм силы, параллельные оси Oz, вклада в крутящий момент не вносят. С силами, лежащими в ( ) поп сечения стержня (интенсивности этих сил — касательные напряжения и 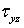) М_z связывает вытекающее из его определения уравнение равновесия статики (рис. 1)Для определения крутящих мом в сечениях пользуются методом сечений. Намечают участки бруса, рассекают его вооброжаемой плоскостью, мысленно отрбрасывают одну часть. К др части прикладывают в сечении неизвестный крут. момент, направляя его по ходу часовой стрелки и составляют уравне равновесия, из которого находят значение Т.Полож принимают скручивающие моменты, если они поворачивают отсеченну часть бруса против хода часовой стрелки. Знак крут момента бруса значения не имеет. M_z положительное, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (рис. 2). Крутящ момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог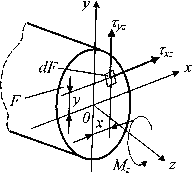

 

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1. Намечаем характерные сечения.

2. Определяем крутящий момент в каждом характерном сечении.

3. По найденным значениям строим эпюру

2.Вывод формулы для определения касат напряжений при кручении стержней круглого поперечного сечения

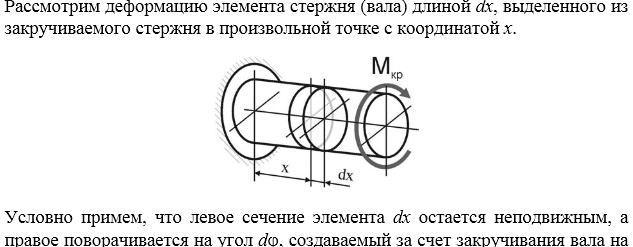
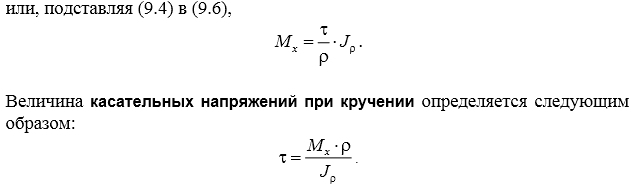
3.Кручение: деформация бруса круглого поперечного сечения; жесткость при кручении; эпюра углов закручивания.

В любом круговом слое поперечного сечения скручиваемого стержня возникают касательные напряжения , которые для цилиндрического стержня можно определить по формуле . Данное выражения явл. уравнением для построения графика, т.е. эпюры касательных напряжений в любом радиальном направлении круглого сечения.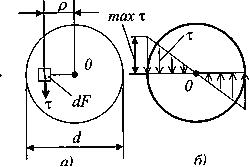

В плоскостях сечений радиальные линии образуют углы поворота сечений φ1 и φ2. Угол ФИ1 свидетельствует о сдвиговой деформации волокон на участке стержня длинной Z, а угол ФИ2 – на участке Z – dz. Приращение угла поворота ФИ на участке стержня dz составляет величину dφ, которую называют углом закручивания стержня, т.е. абсолютной угловой деформацией при кручении. Относительной деформацией при кручении явл. величина θ= dφ/dz.Здесь — погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 6, a)

(2)

Если в круговом слое скручиваемого стержня обнаружена сдвиговая деформация, то в нем должны возникнуть касательные напряжения, которые по закону Гука составлют τ=Gγ или τ=Gρθ. В центре сеченя напряжения отсутствуют.Относительный угол закручивания пропорционален крутящему моменту в сечении и обратно пропорционален жесткости сечения скручиваемого стержня GIp.Для обеспечения необходимой жесткости производится проверка по условию жесткости вида θmax = Tmax/ (GIp) ≤θadm. Нормативные значения θadm находятся в пределах 0,15 – 2 град/м.