15. Які системи можна оцінювати звичайним мнк?

Можна довести, що застосування звичайного МНК до рівнянь структурної форми системи рівнянь призводить до отримання зміщених оцінок параметрів через корельованість (залежність) змінних і залишків моделі, що є порушенням однієї з передумов застосування МНК

Для рівнянь множинної регресії з автокорельованими залишками цю матрицю отримують на підставі залишків моделі, параметри якої оцінено за звичайним МНК

16. У чому полягає суть двокрокового мнк?

Якщо рівняння структурної форми моделі надідентифіковані, то непря­мий метод найменших квадратів застосувати не можна, а користуватись 1МНК недоцільно, тому необхідно розглянути інші методи, які розроблені спеціально для таких моделей. Одним з цих методів є двокроковий метод найменших квадратів (2МНК).

Розглянемо спочатку ідею методу. Вона полягає в тому, щоб «очисти­ти» поточні ендогенні змінні Y від стохастичної складової, бо вони пов’я­зані із залишками u.

Крок 1. Перевіряється кожне рівняння моделі на ідентифікованість. Якщо рівняння надідентифіковані, то для оцінки параметрів кожного з них можна використати оператор оцінювання:

.

Крок 2. Знаходження добутку матриць поточних ендогенних змінних, які містяться у правій частині моделі, на матрицю всіх екзогенних змінних моделі, тобто .

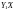Крок 3. Обчислення матриці 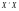і знаходження оберненої матриці .

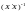Крок 4. Визначення добутку матриць всіх екзогенних змінних і ендогенних змінних у правій частині моделі, тобто .

Крок 5. Знаходження добутку матриць, які здобуто на кроках 2,3,4, тобто .

Крок 6. Визначення добутку матриць ендогенних змінних у правій частині моделі і екзогенних змінних, які внесені до даного рівняння, тобто .

Крок 7. Знаходження добутку матриць екзогенних змінних, які входять в дане рівняння, і ендогенних змінних правої частини системи рівнянь, тобто .

Крок 8. Визначення добутку матриць екзогенних змінних даного рівняння, тобто .

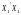Крок 11. Знаходження матриці, оберненої до блочної:

.

Крок 10. Визначення добутку матриць , де — матриця всіх екзогенних змінних моделі, 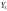— вектор залежної ендогенної змінної лівої частини рівняння.

Крок 11. Знаходження добутку матриць:

.

Крок 12. Визначення параметрів моделі:

.

Крок 13. Обчислення s-ї залежної ендогенної змінної на основі знайдених параметрів і :

.

Крок 14. Обчислення вектора залишків в s-му рівнянні системи:

.

Крок 15. Визначення дисперсії залишків для кожного рівняння:

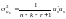
Крок 16. Знаходження матриці коваріацій для параметрів кожного рівняння:

.

Крок 17. Знаходження стандартної помилки параметрів і визначення довірчих інтервалів:

.