7. Запишіть умову ідентифікованності системи рівнянь.

Для ідентифікації моделей зведена форма визначається однозначно за допомогою співвідношень (10.3). Матриця E – A завжди невироджена. Умова ідентифікації має перевірятися для кожного рівняння системи.

Необхідна умова ідентифікації системи – справедливість нерівності для кожного рівняння моделі (10.1):

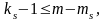(10.10)

де 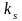 – кількість залежних ендогенних змінних, які входять в s-те рівняння структурної форми;

m – загальна кількість екзогенних змінних моделі;

 – кількість екзогенних змінних, які входять в s-те рівняння структурної форми моделі.

Число екзогенних змінних, які не входять у s-те рівняння структурної форми, дорівнює .

Означення 10.4: Якщо для всіх рівнянь моделі (10.1) співвідношення (10.10) виконується як рівність, то система рівнянь є точно ідентифікованою.

Означення 10.5: Якщо для всіх рівнянь моделі співвідношення (10.10) виконується як нерівність, то система рівнянь є надідентифікованою.

Можна показати, що необхідною умовою ідентифікації певного рівняння є: число змінних, які виключені з рівняння, має дорівнювати числу рівнянь моделі мінус одиниця.

Альтернативна умова ідентифікації була записана нами в (10.10):

яка потребує, щоб число виключених із рівняння екзогенних змінних було не меншим, ніж число ендогенних змінних мінус одиниця.

Необхідною і достатньою умовою ідентифікованості є: у моделі, що містить k рівнянь відносно k ендогенних змінних, умова ідентифікованості виконується тоді і тільки тоді, коли ранг матриці, складеної з виключених з даних рівнянь змінних, але таких, що містяться в інших рівняннях системи, дорівнює k-1.

8. Яка система рівнянь називається надідентифікованою?

Надідентифікованою (переототожненою) називається така модель, що для деяких її параметрів можна отримати кілька кількісних значень на підставі параметрів зведеної форми.

9. Чому звичайний мнк практично не використовується для оцінювання систем одночасних рівнянь?

Можна довести, що застосування звичайного МНК до рівнянь структурної форми системи рівнянь призводить до отримання зміщених оцінок параметрів через корельованість (залежність) змінних і залишків моделі, що є порушенням однієї з передумов застосування МНК. Перехід від структурної форми моделі до скороченої є одним із способів, що усуває проблему корельованості, однак породжує іншу, а саме проблему ідентифікованості окремих рівнянь системи, а також системи загалом.

Залежно від розв'язання цієї проблеми, тобто після перевірки умови ідентифікованості кожного рівняння системи, застосовують такі методи оцінювання параметрів системи:

1) якщо кожне рівняння системи точно ідентифіковане, то параметри зведеної моделі оцінюють непрямим методом найменших квадратів (НМНК); ідея методу полягає в тому, щоб від структурної форми перейти до зведеної, звичайним МНК оцінити параметри останньої й оберненим перетворенням отримати оцінки параметрів структурної форми;

2) усунути кореляцію між змінними та залишками моделі можна також за допомогою методу інструментальних змінних, ідея якого полягає в тому, щоб змінні, що корелюють із залишками, замінити іншими – інструментальними, які тісно пов'язані з незалежними змінними моделі, але зовсім не пов'язані з її залишками;

3) якщо рівняння структурної форми моделі надідентифіковані, то параметри моделі оцінюють за допомогою двокрокового методу найменших квадратів (2МНК), що передбачає виконання двох етапів:

а) перший – ендогенні змінні «звільняють» від стохастичних залишків;

6) другий – оцінені рівняння підставляють у структурну систему рівнянь, до яких потім застосовують звичайний МНК;

4) трикроковий метод найменших квадратів для одночасного оцінювання всіх рівнянь системи за певних обставин ефективніший порівняно з непрямим і двокроковим МНК.

10. На основі якого методу можна оцінити параметри моделі, якщо вона складається із системи рекурсивних рівнянь?

11. Який метод оцінки параметрів можна застосувати, коли всі рівняння моделі є точно ідентифікованими?

1) якщо кожне рівняння системи точно ідентифіковане, то параметри зведеної моделі оцінюють непрямим методом найменших квадратів (НМНК); ідея методу полягає в тому, щоб від структурної форми перейти до зведеної, звичайним МНК оцінити параметри останньої й оберненим перетворенням отримати оцінки параметрів структурної форми;

12. На основі якого методу можна оцінити параметри моделі, якщо вона має надідентифіковані рівняння?

якщо рівняння структурної форми моделі надідентифіковані, то параметри моделі оцінюють за допомогою двокрокового методу найменших квадратів (2МНК), що передбачає виконання двох етапів:

а) перший – ендогенні змінні «звільняють» від стохастичних залишків;

6) другий – оцінені рівняння підставляють у структурну систему рівнянь, до яких потім застосовують звичайний МНК;

13. Чи можна виконувати оцінку параметрів моделі окремо для групи точно ідентифікованих і надідентифікованих рівнянь?

14. У чому полягає суть непрямого методу найменших квадратів?

Оскільки на основі звичайного МНК неможливо отримати якісні оцінки параметрів системи одночасних рівнянь, варто скористатися іншими методами оцінювання параметрів. Одним із них є непрямий метод найменших квадратів, що ґрунтується на використанні зведених рівнянь.

Він складається з двох процедур. Спочатку застосовується 1МНК для оцінки параметрів кожного рівняння зведеної форми моделі (10.7)–(10.8). Основна особливість такої форми полягає в тому, що її здобуто в результаті розв’язування структурної системи рівнянь відносно поточних значень ендогенних змінних, і зведена форма виражає їх як функції всіх інших змінних моделі таким чином, що кожне рівняння в такій формі має поточне значення тільки однієї ендогенної змінної.

Алгоритм непрямого методу найменших квадратів.

Крок 1. Перевіряється умова ідентифікованості для кожного рівняння структурної форми моделі. Якщо кожне рівняння точно індентифіковане, то переходимо до кроку 2.

Крок 2. Кожне рівняння структурної форми розв’язується відносно однієї з k залежних ендогенних змінних моделі, у результаті приходимо до зведеної форми моделі.

Крок 3. На основі 1МНК визначається оцінка параметрів окремо для кожного рівняння зведеної форми.

Крок 4. Розраховується оцінка параметрів рівнянь структурної форми за допомогою співвідношення AR = –B, де A і B параметри структурних рівнянь, а R  – матриця оцінок параметрів зведеної форми.