Що означає зведена форма моделі? Як її одержати?
Якщо економетрична модель застосовується не для аналізу системи, а для передбачення чи оцінювання параметрів, структурна форма моделі неприйнятна. Алгебраїчними перетвореннями систему структурних рівнянь зводять до форми, у якій кожне рівняння містить лише одну ендогенну змінну, яка є функцією від екзогенних змінних. Така форма рівнянь називається зведеною.
Зведену форму рівнянь можна назвати скороченою. Це пов'язано з тим, що при певних перетвореннях багато окремих економічних залежностей можуть бути виключені з розгляду, а отже, загальна кількість рівнянь може скоротитися.
Внаслідок таких перетворень зведена форма рівнянь, на відміну від структурної, не має ні безпосередньої, ні будь-якої економічної інтерпретації. Рівняння у зведеній формі дають змогу передбачити, як зміниться значення ендогенної змінної, якщо змінюватимуться значення екзогенних змінних, однак па підставі цих рівнянь неможливо пояснити, як і чому це відбувається. Саме через це зведену форму рівнянь називають також прогнозною.
Розв’яжемо систему рівнянь (10.1) відносно Y і дістанемо систему виду:
(10.3)
У матричній формі систему цих рівнянь можна переписати так:
(10.4)
Матриця оцінок параметрів R має вигляд:
(10.5)
де E – одинична матриця.
Щоб показати справедливість співвідношення (10.5), розв’яжемо систему рівнянь (10.2) відносно Y:
Y – AY = BX + u; (10.6)
(E – A)Y = BX + u; (10.7)
Y = (E – A)–1BX + u. (10.8)
Враховуючи, що Y = RX + v, R = (E – A)–1B.
Вектор
залишків
є лінійною комбінацією залишків
.
Означення 10.2: Економетрична модель, яка записується системою рівнянь (10.3), називається зведеною формою моделі.
Дайте визначення рекурсивних систем і запишіть модель на основі рекурсивної системи.
Якщо в економетричній моделі (11.2) матриця A має трикутний вид, а залишки характеризуються діагональною матрицею , то така система рівнянь називається рекурсивною.
(11.2)
Нехай економетрична модель на основі одночасових структурних рівнянь запишеться так:
(11.14)
матриця для неї
.
(11.15)
системы рекурсивных уравнений – в которых зависимая переменная одного уравнения выступает в виде фактора в другом:
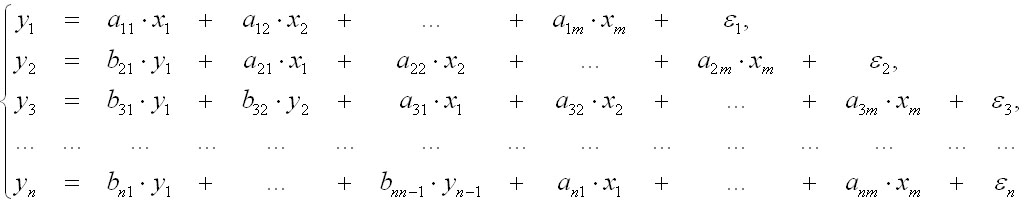
Яка система рівнянь називається точно ідентифікованою?
Проблеми чисельної оцінки параметрів в структурній формі і можливість перетворення структурної форми на зведену тісно пов’язані з поняттям ідентифікованості моделі.
Щоб забезпечити необхідну якість оцінок параметрів (незміщеність, ефективність і обґрунтованість), намагаються па підставі оцінених параметрів скороченої (зведеної) форми системи рівнянь отримати оцінки параметрів структурної форми. Однак тут виникає проблема однозначних залежностей між параметрами: при поверненні від скороченої форми моделі до структурної (обернені перетворення) можна отримати єдине значення шуканого параметра чи кілька різних значень або взагалі не мати змоги отримати жодного.
Щоб передбачити можливі варіанти розв'язання задачі оцінювання параметрів системи одночасних рівнянь, необхідно попередню дослідити модель, а саме перевірити ідентифікованість системи. Під проблемою ідентифікації розуміють можливість чисельної оцінки параметрів структурних рівнянь за оцінками коефіцієнтів зведених рівнянь.
Означення 10.3: Якщо ніяка лінійна комбінація рівнянь структурної форми не може привести до рівняння, що має ті самі змінні, як і деяке рівняння в структурній формі, то модель буде ідентифікованою.
Економетрична модель, задана системою одночасних рівнянь, називається точно (строго) ідентифікованою (ототожненою), якщо однозначно можна отримати оцінки її параметрів на основі оцінених параметрів зведеної моделі.
Надідентифікованою (переототожненою) називається така модель, що для деяких її параметрів можна отримати кілька кількісних значень на підставі параметрів зведеної форми.