Лабораторна робота №7

«ОЦІНКА ПАРАМЕТРІВ СИСТЕМИ ЕКОНОМЕТРИЧНИХ РІВНЯНЬ»

Мета роботи: оцінити параметри системи економетричних рівнянь.

Зміст роботи: дослідити зв’язки між економічними показниками в системі одночасових економетричних рівнянь та провести їх параметризацію.

Завдання до роботи:

– Перевіряється умова ідентифікованості для кожного рівняння.

– Визначити, який з методів може бути використати для параметризації системи рівнянь.

– Оцінити параметри моделі вибраним методом.

– Додатково здійснити розрахунки по знаходженню кореляційної матриці за допомогою MS Excel.

– Для напряму «Економічна кібернетика»: виконати всі дії паралельно в ПП MathCAD або Statistica.

– Провести аналіз побудованої моделі.

Початкові дані:

Економетрична модель складається з двох рівнянь:

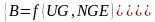(7.1)

Перше рівняння відображає залежність грошового обігу 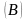від оборотності грошей та грошових доходів населення . У другому рівнянні оборотність грошей визначається у вигляді функції від грошового обігу та розміру вкладу в ощадбанк . Між двома змінними – грошовим обігом та оборотністю грошей – існують одночасні зв’язки, так як кожна з них в одному рівнянні виступає як факторна змінна, у другому – як результативна.

Введемо позначення:

грошовий обіг ;

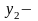оборотність грошей ;

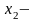грошові доходи населення ;

розмір вкладу в ощадбанк .

Дані про 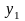, , 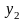, представлено у вигляді відхилень від відповідних середніх у табл. 7.1.

Таблиця 7.1 – Відхилення змінних , , , від їх середніх значень

1	N4-11	N1+4	N3-5	N4+10
2	N1-8	N3+5	N4-2	N3+7
3	N1-7	N4+3	N3-3	N1+1
4	N2-5	N4+1	N2-1	N4+4
5	N1-1	N1+2	N1	N1+1
6	N2+2	N4	N1	N4-3
7	N3+4	N4 -2	N4+2	N2-6
8	N1+3	N3 -4	N2+2	N3-4
9	N1+6	N3 -5	N3+3	N4-9
10	N4+7	N2 -4	N4+4	N3-11

N₁, N₂, N₃, N₄ вибираються з наступної таблиці:

Варіант	N1	N2	N3	N4
1	7	6	1	7
2	7	7	2	2
3	2	6	8	6
4	7	6	4	7
5	4	8	3	4
6	3	2	6	8
7	3	3	3	7
8	4	5	6	5
9	7	4	2	9
10	8	8	1	8
11	7	3	6	3
12	4	3	7	7
13	3	6	6	4
14	4	8	5	3
15	3	3	4	2
16	5	6	8	1
17	8	5	7	8

Необхідно оцінити параметри економетричної моделі (7.1).

Вимоги до звіту: назва, тема, мета, завдання, розрахункові формули. Результати аналітичного розв’язання задачі та комп’ютерного у вигляді таблиці MS Excel з вихідними умовами експерименту, таблиці MS Excel з результатами обчислень, висновок про отримані результати. Опис інструментів та функцій MS Excel, що використовувались при вирішенні задачі. Короткий опис технології вирішення задачі в MS Excel (для напряму «Економічна кібернетика» – опис технології вирішення задачі в ПП MathCAD або Statistica).

Контрольні питання:

1. Які основні причини використання систем одночасних рівнянь?

Многие экономические взаимосвязи допускают моделирование одним уравнением. В большинстве случаев использование МНК для оценки параметров таких моделей является наиболее подходящей процедурой. Однако ряд экономических процессов моделируется не одним, а несколькими уравнениями,

содержащими как повторяющиеся, так и собственные переменные. В силу этого

возникает необходимость использования систем уравнений. Кроме того, в одних уравнениях определенная переменная может рассматриваться как объясняющая (

независимая), но в то же время она входит в другое уравнение как зависимая ( объясняемая) переменная.

2. У чому полягає основна розбіжність між структурними рівняннями сситеми и рівняннями у зведеній формі?

Економетрична модель у вигляді (10.1) безпосередньо відображає структуру зв’язків між змінними і тому називається структурною формою економетричної моделі.

Структурна форма економетричної моделі описує одно- та багатосторонні стохастичні причинні співвідношення між економічними величинами в їх безпосередньому вигляді. Вона містить усю суттєву інформацію про залежності між економічними явищами та процесами. Кожне співвідношення такої системи (рівняння чи тотожність) має певну економічну інтерпретацію.

Економетрична модель називається повною, якщо:

а) вона охоплює змінні, що суттєво впливають на спільно залежні змінні, а вектор залишків має випадковий характер;

б) містить стільки рівнянь, скільки в ній є спільно залежних змінних, тобто кожна залежна змінна пояснюється окремим рівнянням;

в) система рівнянь має однозначний розв'язок відносно спільно залежних змінних, тобто матриця (E – A) в моделі (10.2) невироджена (має відмінний від нуля визначник).

Повна модель застосовується у випадках, коли необхідно кількісно описати економічне явище чи процес або спрогнозувати їх розвиток.

Якщо економетрична модель застосовується не для аналізу системи, а для передбачення чи оцінювання параметрів, структурна форма моделі неприйнятна. Алгебраїчними перетвореннями систему структурних рівнянь зводять до форми, у якій кожне рівняння містить лише одну ендогенну змінну, яка є функцією від екзогенних змінних. Така форма рівнянь називається зведеною.

Зведену форму рівнянь можна назвати скороченою. Це пов'язано з тим, що при певних перетвореннях багато окремих економічних залежностей можуть бути виключені з розгляду, а отже, загальна кількість рівнянь може скоротитися.

Внаслідок таких перетворень зведена форма рівнянь, на відміну від структурної, не має ні безпосередньої, ні будь-якої економічної інтерпретації. Рівняння у зведеній формі дають змогу передбачити, як зміниться значення ендогенної змінної, якщо змінюватимуться значення екзогенних змінних, однак па підставі цих рівнянь неможливо пояснити, як і чому це відбувається. Саме через це зведену форму рівнянь називають також прогнозною.

3. Запишіть в загальному вигляді структурну форму моделі на основі одночасових рівнянь.

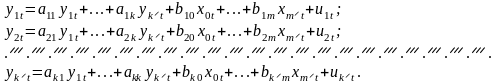(10.1)

У цій моделі 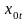=1. Окремі коефіцієнти ..., , ..., можуть дорівнювати нулю, якщо відповідна змінна не входить до рівняння. Залишки , де s = 1,2, ..., k, також можуть дорівнювати нулю, якщо відповідне рівняння є тотожністю. Систему (10.1) можна переписати в матричній формі

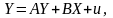(10.2)

де Y – вектор ендогенних залежних змінних;

X – матриця екзогенних пояснювальних змінних;

u – вектор залишків;

A – матриця коефіцієнтів при змінних Y розміром k × k;

B – матриця коефіцієнтів при змінних X розміром k × m;

Змінні, які містяться в правій частині системи рівнянь, є наперед заданими (вхідними) і називаються екзогенними, а змінні, які містяться в лівій частині, знаходяться в результаті реалізації моделі і називаються ендогенними. Отже, змінна у є ендогенною для одного рівняння і одночасно екзогенною для іншого.