8. Молекулярная диффузия. Первый закон Фика. Коэффициент диффузии и его физический смысл.

Молекулярная диффузия (массопровоность) – передача вещества за счёт перемещения молекул.

Молекулярная диффузия в газах и растворах жидкостей проис­ходит в результате хаотического движения молекул, не связанного с движением потоков жидкости. В этом случае, т. е. когда концентра­ции перемещающихся в пространстве молекул малы, препятствий к взаимосвязанному их перемещению нет. В результате имеет место перенос молекул распределяемого вещества из областей высоких концентраций в область низких концентраций. Кинетика переноса подчиняется в этом случае первому закону Фика: количество вещества, переданное за счет молекулярной диффузии, пропорционально градиенту концентраций поверхности контакта фаз и количеству времени на осуществление процесса: dM=-D*(δc/δn)*dFdτ.

dM-кол-во продифунд.в-ва;D-коэф.диффузии.

Знак минус в правой части уравнения показывает, что при молекулярной диффузии в направлении перемещения вещества концентрация убывает.

D показывает, какое количество вещества диффундирует через поверхность 1м² в течение 1с при разности концентраций на расстоянии 1м, равной единице.

Коэффициент диффузии зависит прежде всего от агрегатного состояния систем: так, коэффициент диффузии для газов примерно на четыре порядка выше, чем для жидкостей. Коэффициент диффузии увеличивается с ростом температуры и уменьшается с повышением давления.

9. Уравнение Щукарева. Коэффициент массоотдачи и его физический смысл. Сопоставление с коэффициентом массопередачи.

Конвективная диффузия осуществляется за счет перемещения молей вещества от потока к стенке. Подчиняется массоотдача закону Щукарева-Нернста: кол-во вещества, переданного за счет массоотдачи, пропорционально разности концентраций у границы раздела фаз и в ядре потока поверхности контакта фаз и времени проведения процесса.

В основу рассмотрения явления конвективной диффузии поло­жена теория диффузионного граничного слоя. Согласно этой теории, распре­деляемое вещество переносится из ядра по­тока жидкости к границе раздела фаз непо­средственно потоками жидкости и молеку­лярной диффузией. В рассматриваемой системе поток можно считать состоящим из двух частей: ядра и граничного диффузионного слоя. В ядре перенос вещества осуществляется преимущественно токами жидкости и в усло­виях достаточной турбулентности течения; концентрация распределяемого вещества в данном сечении сохраняется постоянной.

dM=β(Cr-Cf)dF*dτ

β[м/с]-коэф массоотдачи, хар-т перенос в-ва конвективными и диф-ми потоками одновременно, показывает какое кол-во в-ва передается от пов-ти раздела фаз в воспринимаемую фазу через 1м² фазового контакта в течении 1с при разности концентраций 1кг/м³.

Сr-конц-я в воспринимаемой фазе у поверхности раздела фаз

Сf-конц-я в ядре потока воспринимающей фазы.

Концентрация на границе Сr рассматривается как равновесная концентрация. Коэффициент массоотдачи зависит от гидродинамической обстановки.

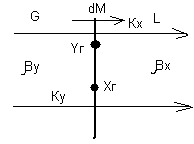
Связь коэф. массопередачи и массоотдачи.

Допущения: 1. Процесс стационарный; 2. Равновесная линия прямая ур=Арх; 3. Концентрации на границе фаз являются равновесными.

хг=хрг; уг=ург; х=ур/Ар

Количество распределяемого вещества, перемещающегося из фазы G к элементу поверхности на границе раздела фаз: dM=β_y (y-y_г)dF, β_y -коэффициент массоотдачи для фазы G.

То же количество распределяемого вещества, перемещающегося от элемента поверхности на границе раздела фаз в фазу L: dM=β_x(х_г-х)dF, β_x -коэффициент массоотдачи для фазы L.

Равновесная зависимость: у_р=А_рх→х=у_р/А_р; х_г=у_рг/А_р

dM= β_x (х_г-х)dF= (β_x /А_р)(у_рг-у_р)dF

для L: (у_г-у_р)=(dM/dF) ( A_р/ β_x) (1)

для G: (y-y_г)=(dM/dF) ( 1/ β_y) (2)

Складываем (1) и (2), получим: y-y_р=(dM/dF) ( A_р/ β_x + 1/ β_x)

dM=[1/ ( A_р/ β_x + 1/ β_y)] (y-y_р)dF (3)

Основное уравнение массопередачи имеет вид:

dM=К_y (y-y_р)dF (4)

Сравнивая (3) и (4), получим: K_y=1/ (1/ β_y+ Aр/ β_x)

K_х=1/ ( 1/ β_x + 1/Ap β_y)

β_y- коэф массоотдачи из потока газа к пов-ти фазового контакта

β_x-коэф массоотдачи от пов-ти фазового контакта к потоку жидкости.