5. Термодинамические потенциалы.
Все
расчеты термодинамики основываются
на использовании функций состояния,
называемыми Термодинамическим
потенциалом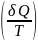. ds=
;
δQ=Tds;
SQ=du+δA; Tds=du+δA=du+pdV
Внутренняя
энергия: du=Tds-δA=Tds-pdV;
;
;
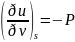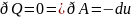(при адиабатном процессе)
Свободная
энергия (Гельмгольца): F=U-Ts;
dF=du-Tds-sdT;
T=const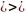
dF=du-Tds=Tds-pdv-Tds=-pdv;
δA=-dF;
dF=Tds-pdv-Tds-SdT=-pdv-sdT;
;
;
Энтальпия: H=u+pv;
dH=du+pdv+vdp=Tds-pdv+pdv+vdp=Tds+vdp;
;
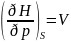изобарный
пр. P=const
.
Поскольку
в Изобарном
процессе работа
равна PΔV, приращение энтальпии
в
Квазистатическом изобарном
процессе равно количеству теплоты,
полученному системой.
Потенциал
Гиббса: G=u-Ts+pv;
dG=du-tds-sdT+pdv+vdp=Tds-pdv-Tds-sdT+pdv+vdp=-sdT+vdp;
;
Необратимое
термодинамическое неравенство:
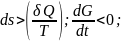
Сопровождается
уменьшением
потенциала Гиббса, таким
образом
равновесным будет являться состояние
для которого термодинамического
потенциалаГиббса будет минимальна.
Изменение
внутренней
энергии может происходить ещё и в
процессе массы обмена.
;
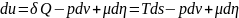μ=
хим.
пот-ал-это изменение
энергии
системы, при изменении на единицу числа
частицы
системы,
при азохорно и изотермическом процессе
μ=
6. Уравнение кинетической теории газов. Энергия молекул газа.
Теория, основанная на статистическом методе исследования физ. св-в. газов называется кинетической теорией газов. 1) В системевыполняются законы
сохранения, импульса, момента импульса. 2) Все системы частицы являются меченными, т.е. можно определить другот друга одинаковые молекулы. 3) Все
физические процессы протекают в пространстве времени непрерывно (в отличии квантовыхстатистик). 4) Каждая частица может иметь совершенно
произвольные значения координат и компонент скорости (независимо от соседей).Основными доказательствами положений МКТ стали: диффузия,
вязкость, теплопроводность. Идеальный газ можно рассматривать, каксовокупность беспорядочно движ. Молекул шариков. Имеющих приближенно малые
собственно
объем и не взаимодействует друг с
другом. Число ударов молекул об единичную
площадку в единицу времени:
;
импульс
отданной
стенке:
;
-масса
молекул.
;
;
;
-
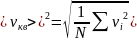среднее значение кинетической энергии
поступ. движ-я.
;
;
k-постоянная
Больцмана 1,38*10-23Дж/К;
R-газовая
постоянная 8,31 Дж/моль*К.
;
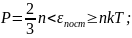
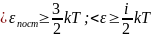i=iпост+iвращ.+2iколеб.
Абсолютная
температура пропорциональна энергии
поступательного движения. Числомстепеней
свободы
механической системы называют количество независимых величин, с помощью которых может быть задано положениесистемы энергией колебательного
движения. Закон равного распределения энергии по степеням свободы: на каждую степень свободымолекулы приходится в среднем одинаковая
кинетическая
энергия равная
.
Внутренняя энергия одного моля газа:
;
;
;
;
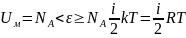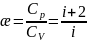
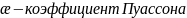
7. Распределение Максвелла.
МКТ предполагает, что в газе находящемся в состоянии равновесия при постоянной температуре устанавливается некоторое стационарное распределение
по
скоростям, которое подчиняется закону
Максвелла. Закон Максвелла описывается
функцией распределения молекул
поскоростям:
;
;Должно
сохраняться условие:
;
;
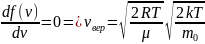