
- •До розрахунково-графічної роботи
- •2.1. Мета роботи...............................................................................................................................15
- •3.1. Мета роботи...............................................................................................................................17
- •4.1. Мета роботи...............................................................................................................................21
- •5.1. Мета роботи...............................................................................................................................21
- •Завдання
- •Календарний план
- •Індивідуальні завдання
- •Список скорочень
- •Розділ 1. Моделі геометрії просторових об’єктів
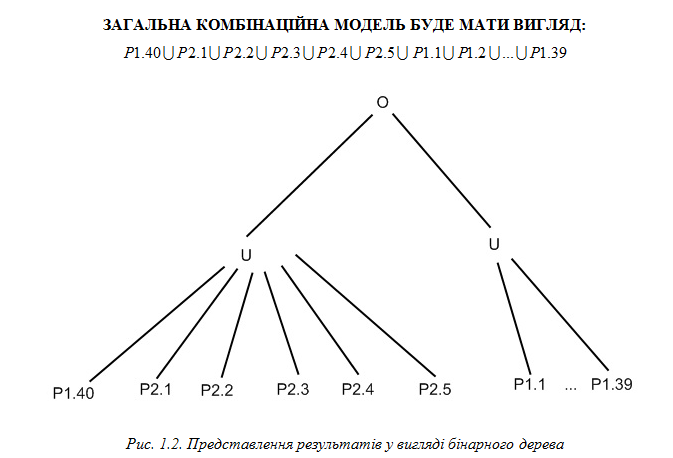
- •1.2. Комбінаційні моделі геометричного об’єкта Комбінаційна модель геометричного об’єкта
- •Розділ 2. Координатне перетворення
- •Розділ 3. Побудови кривих
- •Розділ 4 колірні моделі. Змішування кольорів
- •4.2. Розрахунок кольорів та колірних перетворень
- •1. Тексти програмної реалізації завдання:
- •Int main(void)
- •2. Результати виконання програми (PrintScreen):
- •Розділ 5 програмні реалізації
- •5.2. Програмна реалізація з OpenGl
- •InitializeComponent();
- •5.2.2 Віконні інтерфейси
- •5.3. Програмна реалізація з WinApi
- •5.3.1 Опис алгоритму
- •Interface
- •Image1: tImage;
- •Implementation
- •Var daDi:integer;
- •If Form1.CheckBox2.Checked then
- •5.3.2 Віконні інтерфейси
- •5.4. Програмна реалізація афінних перетворень та анімації
- •5.4.1 Опис алгоритму
- •2. Тексти програмної реалізації завдання:
- •Void drawB()
- •Void DrawObjects()
- •Int main( int argc, char *argv[])
- •5.4.2 Віконні інтерфейси
- •5.5. Програмні реалізація розрахунків кривих ліній, координат, кольорів
- •5.5.1 Опис алгоритмів
- •Int main(void)
- •5.5.2 Віконні інтерфейси
- •Висновки
- •Список використаних джерел
- •Додатки
- •InitializeComponent();
- •Interface
- •Image1: tImage;
- •Implementation
- •Var daDi:integer;
- •If Form1.CheckBox2.Checked then
- •Void drawB()
- •Void DrawObjects()
- •Int main( int argc, char *argv[])
- •Int main(void)
Розділ 1. Моделі геометрії просторових об’єктів
1.1. Мета роботи - ознайомитись з моделями, які використовуються для опису геометрії просторових об’єктів при геометричному проектуванні. Вивчити методи опису поверхонь та складних форм та структур, набути практичних навиків побудови каркасних моделей, моделей на основі комбінації суцільних примітивів.
1.2. Комбінаційні моделі геометричного об’єкта Комбінаційна модель геометричного об’єкта
Розбиваю суцільну модель (об’єкт)– водяний годинник на прості складові – примітиви наприклад призми, циліндри. Примітиви можуть просторово комбінуватися один з одним, утворюючи більш складні форми, які називається будівельними блоками чи просто блоками. Блоки забезпечують створення функціональної деталі чи цілого вузла.
Даний суцільний об’єкт можна розділити на дві складові:
· Корпус;
· Механізм;

Рис. 1.1 Зображення змодельованого пристрою
1.3. Каркасні моделі геометричного об’єкта



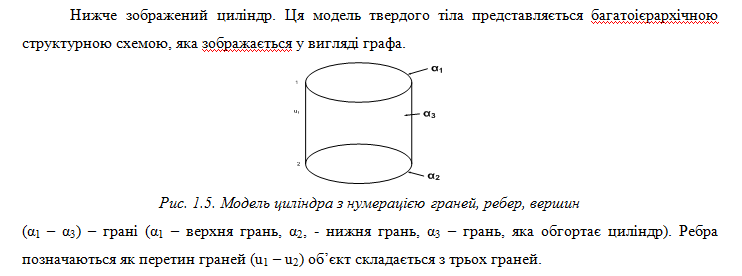
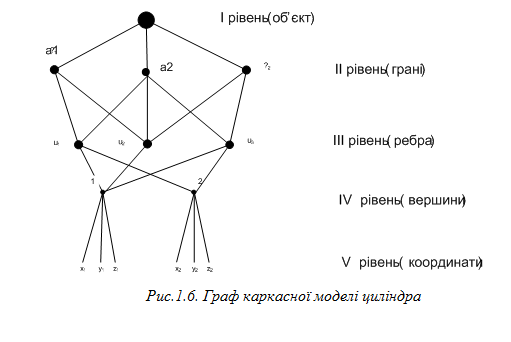
1.4. Матриці суміжності
Таблиця 1.1 Матриця суміжності

Таблиця 1.2 Матриця суміжносвті паралепіпеда
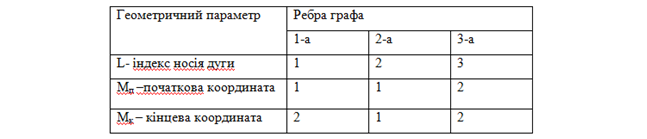
1.5. Матриці інцедентності
Таблиця 1.3 Матриця інцедентності
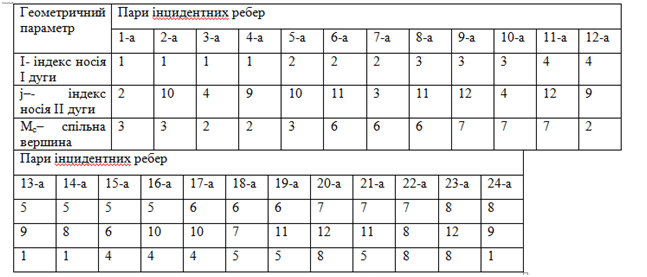 Таблиця
1.4 Матриця інцедентності циліндра
Таблиця
1.4 Матриця інцедентності циліндра

Розділ 2. Координатне перетворення
2.1. Мета роботи - ознайомитись з координатними системами, які використовуються у геометричному моделюванні. Вивчити методи опису координат, набути практичних навиків переводу координат з однієї системи в іншу.
2.2. Розрахунок координат та перетворень





2.3. Графічні побудови координатних систем та перетворень
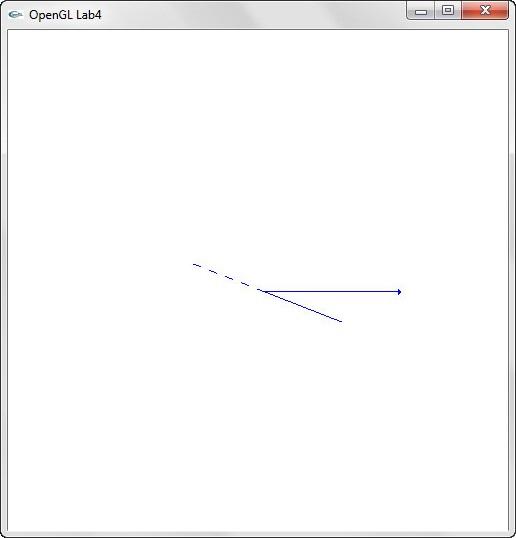
Рис. 2.1 Виконання завдання а)
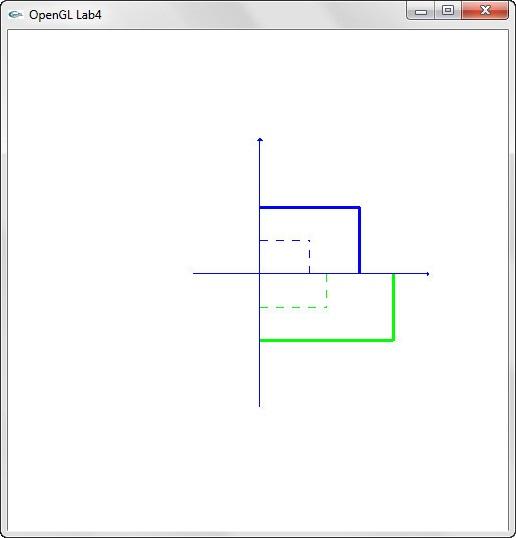
Рис. 2.2 Виконання завдання б)
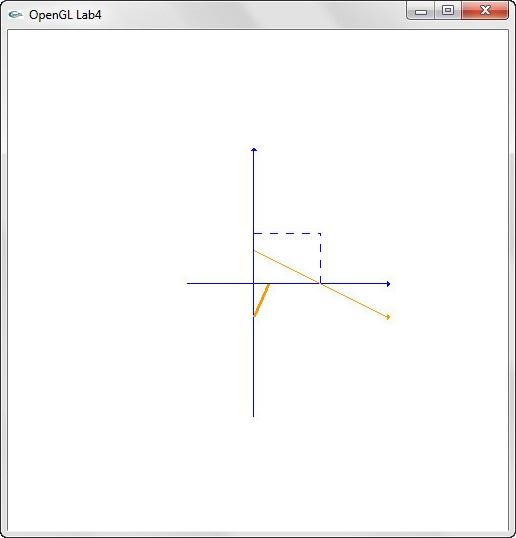
Рис. 2.3 Виконання завдання в)

Рис. 2.4 Виконання завдання ґ)
Розділ 3. Побудови кривих
3.1. Мета роботи - ознайомитись з задачами конструювання кривих. Вивчити метод побудови кривої Без’є заданої вершинами багатокутника.
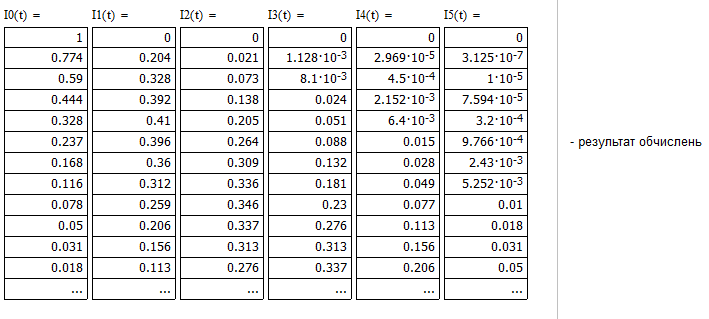
3.2. Розрахунок класичних кривих

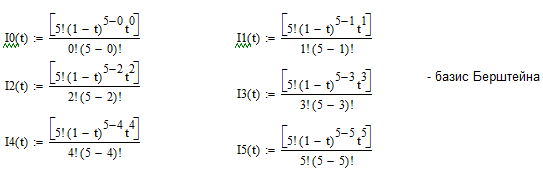

3.3. Графічні побудови класичних кривих
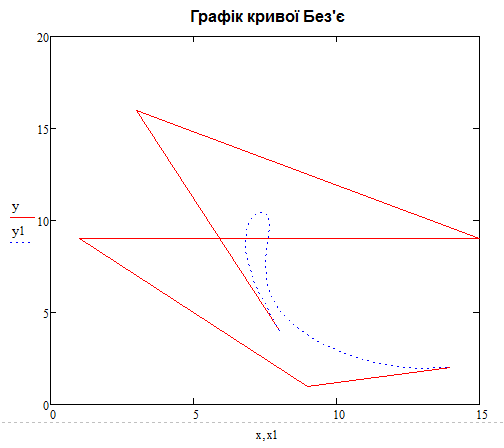
Рис. 3.1 Графік кривої
3.4. Розрахунок кривої Без’є

Рис. 3.1 Графік кривої в емуляторі
Розділ 4 колірні моделі. Змішування кольорів
4.1. Мета роботи - ознайомитись з колірними моделями, які використовуються у комп’ютерній техніці, телебаченні, геометричному проектуванні поліграфії. Вивчити методи опису визначених колірних областей спектру, набути практичних навиків переводу кольору з одної колірної моделі в іншу.
4.2. Розрахунок кольорів та колірних перетворень
1. Тексти програмної реалізації завдання:
#include <math.h>
#include <stdio.h>
#include <conio.h>
Int main(void)
{
float R,R1,G,G1,B,B1,H,L,S; // Оголошення змінних
printf("Vvedit R : "); // Введення R
scanf("%f", &R);
printf("Vvedit G : "); // Введення G
scanf("%f", &G);
printf("Vvedit B : "); // Введення L
scanf("%f", &B);
S=sqrt(pow(R,2)+pow(G,2)+pow(B,2)-R*G-B*G-R*B); // Обчислення S
H=asinf(sqrt(3.0/2.0)*((G-R)/S)); // Обчислення H
L=(R+G+B)/3; // Обчислення L
R1=0.35*220+0.42*20+0.2*60; // Обчислення R`(множення матриці)
G1=0.715*220+0.06*20+0.22*60; // Обчислення B` (множення матриці)
B1=0.1156*220+0.34*20+0.54*60; // Обчислення G` (множення матриці)
R1=R1-R1*0.33; // R`-темніший на тритину
G1=G1-G1*0.33; // G`-темніший на тритину
B1=B1-B1*0.33; // B`-темніший на тритину
printf("\nZavdanie A ");
printf("\n\nZnachenie R`: "); // Вивід R`
printf("%0.2f",R1);
printf("\nZnachenie G`: "); // Вивід G`
printf("%0.2f",G1);
printf("\nZnachenie B`: "); // Вивід B`
printf("%0.2f",B1);
printf("\n\nZavdanie B (RGB - HLS)");
printf("\n\nZnachenie H: "); // Вивід H
printf("%0.2f",H);
printf("\nZnachenie L: "); // Вивід L
printf("%0.2f",L);
printf("\nZnachenie S: "); // Вивід S
printf("%0.2f",S);
getch();
}
