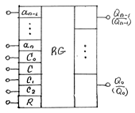
- •Metoda împărţirii succesive
- •Metoda îmulţirii succesive
- •Metoda substituţiei cu calcule în baza nouă
- •Metoda substituţiei automate
- •Intrati:
- •I ntrari:
- •Iesiri md:
- •Determinarea corecta a semnului rez:
- •Determinarea corectitudinii rez:
- •Unit de mem perm:
- •Incrementarea, Decrimentarea datelor
- •I niţializare Se efectueaza pt bistab, rg, contoare. Pt initializare e nec de a şterge inf din rg. În cazul cănd este nec ca la ieşire rg să fie unitatea se face op de instalare în starea unitate.
1 |
Definirea”informatica” și ”informația”. Proprietățile informației, attributive, programatice, dinamice. |
Noţiunea de informatică a apărut ca domeniu al ştiinţei în 1965 în Franţa, provine de la cuvîntul „Informatique”= information + automatique. Definiţia noţiunii „informatică” depinde de modalitatea de abordare.
Definiţia enciclopedică: Informatica este un domeniul al ştiinţei care se ocupă cu studierea structurii şi proprietăţile generale ale informaţiei + modalităţile de colectare, păstrare, prelucrare şi distribuire a cesteia în diverse domenii ala activităţii umane. Cea mai obiectivă definiţie a noţiunii a informaticii este considerată cea a lui Gruşcov: „ Informatica este un domeniu al ştiinţei ce are drept scop cercetarea şi satisfacerea necesităţilor informaţionale ale societăţii umane, iar tehnica de calcul este un mijloc efactiv pentru accelerarea satisfacerii acestor necesităţi.
Noţiunea „informaţie „ provine de la cuvîntul latin „informatio” ceia ce înseamnă comunicare, ştire, mesaj. Definiţia filozofică : Informaţia este o reflectare a lumii reale sau imaginare prin intermediul semnalelor, simbolurilor.
Definiţia practică: informaţia este privită ca cunoştiinţe care pot fi primite, prelucrate şi transmise. Conţinutul informaţiei poate fi caracterizat de următorii parametri: autenticitate, deplinătate, actualitate, calitate, cantitate.
PROPRIETĂŢILE INFORMAŢIEI:
Proprietăţile atributive - proprietatea fără de care informaţia nu poate să existe:
Inseparabilitatea de suportul fizic şi limbaj;
Discretitatea şi continuitatea inform.
Orice informaţie poate fi plasată pe un suport şi descrisă într-un anumit limbaj, informaţia constă din cunoştiinţe despre anumite fenomene, acestea se acumulează treptat, astfel se explică proprietatea de descretitate. Cunoştiinţele acumulate se transmit prin fragmente, însă perceperea informaţiei necesită o consecutiviate continuu.
Proprietăţi pragmatice caracterizează utilitatea informaţiei şi proprietăţile de cumulare. Utilitatea informaţiei se determină prin efectul care poate fi obţinut în rezultatul utilizari acestei informaţiei. Utilitatea poate fi exprimată prin probabilitatea rezolvării careva probleme şi poate fi redată prin formula:
I=log p2 - log p1 = log p2/p1, unde:
p1 – probabilitatea rezolvării problemei în condiţiile iniţiale; p2 – probabilitatea rezolvării problemei în rezultatul utilizării informaţiei propuse.
Utilitatea poate fi pozitivă, nulă, negativă. În caz că utilitatea este negativă informaţia se numeşte dezinformaţie. La etapele de circulaţie a informaţiei se menţine tendinţa de a reda esenţa informaţiei, astfel se manifestă proprietatea de cumulare: E = I/Q
Proprietăţi dinamice – dintre ele se menţionează următoarele:
De creştere
De distribuţie multiplă
De utilizare multiplă
De învechire
De dispariţie
2 |
Măsurarea inform. Unitățile de măsură a inform. Unitățile structurale de măsură a inform Unitățile statistice de măsură a inform. Probabilitatea și entropia. Unitățile semantice de măsură a inform. Excedența, consistența și unitatea inform. |
În teoria informaţiei unităţile de măsură trebuie să respecte trei aspecte:
Aspectul structural cercetează configuraţia discretă a masivelor de informaţie şi măsurarea lor prin numărarea elementelor.
Aspectul static operează cu noţiunea de entropie, drept mărime nedetrminată care scontează probabilitatea apariţiei şi ca urmare calitatea surselor de informaţie.
Aspectul semantic indică utilitatea şi valoarea informaţiei.
Unităţile statistice de măsură a inf: Cea mai răspîndită e unitatea aditivă logaritmică binară de măsură - prezintă cantitatea de inf în unităţi binare – biţi.
Unitatea geometrică de măsurare: Definirea cantităţii de inf prin metoda geometrică se reduce la măsurarea lungimei liniei, suprafeţei planului sau volumul modelului geometric al complexului informaţional dat în unităţi discrete – cuante.
Unitatea combinatorică de măsurare a inform: se utilizează în cazul cînd este necesar de a evalua posibilitatea de transferare a inform cu ajutorul diverselor combinaţii de elemente informaţionale.
Unitatea de măsură aditivă:
Adîncime h- cantitatea de elemnte diferite care se conţin în alfabetul dat.
Lungimea l – nr. de celule numerice suficient p-ru prezentarea numărului de o mărime indicată. După Hartley cantitatea de infor se calculerază: I=log2Q=log2hl .
Unitate aditivă logaritmică de măsură a inform egală cu 1 bit aşa o cantitate de inform a unui nr. pentru care l=1 şi h=2. O grupă de 4 biţi se numeşte nibble, o grupă de 8 biţi se numeşte octet sau byte.
Unităţile statistice de măsură
Probabilitatea: Din punct de vedere al probabilităţii informaţia este privită drept o comunicare despre apariţia sau nu a unor evenimente,realizarea sau nu a unor mărimi şi funcţi, iar cantitatea inform depinde de probabilităţile evenimentelor. Vom numi ansamblu de evenimente un grup finit de evenimente incompatibile cu o repartizare cunoscută a probabilităţii, suma cărora este egală cu o unitate.
Entropie - se utiliz în diferite domenii de ştiinţă şi caracterizează mărimea probabilităţii apariţiei evenimentului. În informatică entropia caract. posibilitatea sursei în prezentarea informaţiei.
Unităţile semantice de măsură: În teoria semantică informaţia este caract prin consuistenţă şi utilitate. Unitatea de măsură as consistenţiei inform se înseamnă prin cont. Consistenţa evenimentului i poate fi exprimată prin funcţia de măsură m(i) în modul următor: cont(i)=m(~i)=1-m(i), i – evenimentul analizat; m – functia de masurare; ~ - semnul negarii
Utilitatea informaţiei se determină prin efectul care poate fi obţinut în rezultatul utilizari acestei informaţiei. Utilitatea poate fi exprimată prin probabilitatea rezolvării careva probleme şi poate fi redată prin formula: I=log p2 - log p1 = log p2/p1, unde: p1 – probabilitatea rezolvării problemei în condiţiile iniţiale; p2 – probabilitatea rezolvării problemei în rezultatul utilizării informaţiei propuse.Utilitatea poate fi pozitivă, nulă, negativă. În caz că utilitatea este negativă informaţia se numeşte dezinformaţie.
3 |
Clasificarea sitem de num. Sisteme poziționale uniforme și mixte de numerație. Conversii între baze de numerație. |
Sistem de numeraţie reprezintă totalitatea regulilor folosite pentru scrierea numerelor cu ajutorul unor simboluri numite cifre.
SN se împart: SN nepoziţionale (sistemul roman)
SN poziţionale (zecimal, binar, octal,hexazecimal)
SN poziţionale se împart în SN poziţionale uniforme şi SN poziţionale mixte. În SN poziţional uniform cel mai semnificativ este SN zecimal, în acest sistem aportul unei cifre la valoarea numărului depinde de valoarea ei, cît şi de poziţia pe care o ocupă . În SN poziţionale mixte numărul cifrelor admise pentru fiecare poziţie poate fi diferit, aceste sisteme sunt utilizate pentru reprezentarea timpului.
În sistemele poziţionalencifrele au o pondere diferită în dependenţă de poziţia pe care o scupă, în general numărul reprezentat într-un SN poziţional are urmat. formă:
N=a n-1,a n-2,...a0,a-1, a-2......am
Dacă luăm în consideraţie baza în care este reprezntat număru atunci valoarea lui este:
N=+-( a n-1 b n-1+a n-2b n-2+....+a-1b-1+.....a-mb-m)
Unde: ai - cifra situata pe poziţia i
b – baza SN; n – nr de cifre în partea întreagă;
m – nr de cifre în partea fracţională; a n-1 - cifra cu ponderea cea mai mare (cea mai semnificativă);
a-m – cifra cu punderea cea mai mică (mai puţin semnificativa).
Conversii între baze de numeraţie
Pentru efectuarea conversiei sunt utilizate următoarele metode:
Metoda împărţirii succesive
Transformarea numerelor din SN zecimal în SN binar, octal, hexazecimal.
Metoda se aplică pentru transformarea părţii întregi a numărului real. Constă în:
Se împarte succesiv numărul dat la baza SN nou;
Împărţirea se opreşte cînd cîtul devine zero, evidenţind resturile obţinute la fiecare etapă.
Rezultatul reprezintă şirul format din valorile resturilor în ordinea inversă a calculelor.
Metoda îmulţirii succesive
Se aplică la transformarea părţilor fracţionare a numerelor zecimale în baza 2,8,16. Constă în: - se îmulţesc succesiv părţile fracţionare a numărului cu baza SN nou;
Se evidenţiază părţile întregi, procedeul continuă pînă la apariţiia unei din cele 3 situaţii:
Obţinerea valorii întregi
Efectuarea unui anumit număr de paşi stabilit în condiţie
Repetarea periodică a valorilor
Rezultatul îl reprezintă şirul format din părţile întregi în ordinea efectuăriilor calculelor.
Metoda substituţiei cu calcule în baza nouă
Transformarea numerelor din orice bază în baza 10: Se aplică formula de calculare a valorii numerice a numărului în baza b scrisă în formă desfăşurată
Metoda substituţiei automate
Transformarea numerelor din baza 2 în baza 8,16
Se grupează cifrele binare cîte 3 (cîte 4) pentru partea întreagă de la dreapta spre stînga, p-ru partea fracţionară de la stînga la dreapta
Fiecare grup de cifre binare se substituie cu o cifră octală (hexazecimală)
Transformarea numerelor din baza 8, 16 în baza 2: Fiecare cifră octală (hexazecimală) se substituie cu un grup de 3 (4) cifre binare. Rezultatul reprezintă şirul obţinut din aceste grupuri.
Transformarea numerelor din baza 8 în baza 16 şi invers
Transformarea se va efectua prin intermediul transformării în baza 2. Îmbinarea regulilor 1 şi 2 (mai întîi 2 şi apoi 1).
4 |
Oper aritmetice în diferite baze de numerație (+, -, *, /). |
Adunarea:
SN binar: se îndeplineşte conform regulilor cunoscute în SN zecimal.
0+0=0 1+1=10
1+0=1 10+1=11
0+1=1 11+1= 100
Ex: 1111,01101
+ 11,11000
10011,00101
SN octal: se face conform tabelului sau se transformă în binar şi se efectuează scăderea şi apoi rezultatul se transformă din binar în octal.
Ex: 362,064
- 5,173
354,671
SN hexazecimal: se face conform tabelului sau se transformă în binar şi se efectuează adunarea şi apoi rezultatul se transformă din binar în hexazecimal.
A37,E1
+ B,F65
A43,D75
Scăderea:
SN binar: se îndeplineşte conform regulilor cunoscute în SN zecimal.
1-0=0
0-0=0
1-1=0
0-1= nu exista
10-1=1
Ex: 11000101,11
- 111,101
10111110,001
SN octal: se face conform tabelului sau se transformă în binar şi se efectuează adunarea şi apoi rezultatul se transformă din binar în octal.
Ex: 357,12
+ 63,7
443,02
SN hexazecimal: se face conform tabelului sau se transformă în binar şi se efectuează adunarea şi apoi rezultatul se transformă din binar în hexazecimal.
15 16 16
Ex: BE0,53
+ A,F65
BD5,5D
Îmulţirea:
SN binar: se îndeplineşte conform regulilor cunoscute în SN zecimal.
0*0=0
1*0=0
0*1=0
1*1=1
Operaţia de împărţire se reduce la o succesiune de înmulţiri şi scăderi. Împărţirea în sistemul hexazecimal se îndeplineşte cu mult mai uşor prin conversia numerelor hexazecimale în binare sau zecimale şi invers.
Ex: Adunarea în binar a numerelor zecimale 29 şi 43:
(29)10=(11101)2; (43)10=(101011)2; transformate în binar se adună: 11101+101011=1001000.
Ex: Scăderea în binar a numărului zecimal 29 din numărul zecimal 43:
(43)10=(101011)2; (29)10=(11101)2; ; transformate în binar se scad: 101011-11101=1110
Ex: Înmulţirea în binar a numerelor zecimale 29 şi 43:
(29)10=(11101)2; (43)10=(101011)2; ; transformate în binar se înmulţesc: 11101 x 101011=10011011111
La înmulţire virgula care desparte partea întreagă de cea fracţionară se fixează ca şi în sistemul de numeraţie zecimal.
5 |
Codificarea inform. Coduri numerice. C. unipolare ponderate. C. bipolare ponderate (EBCDIC binar și hexazecimal, ASCII, ASCII extins). |
Informaţia destinată prelucrării, prealabil trebuie transpusă şi adaptată prorprietăţilor fizice ale aparatajului utilizat. Ex3mple de transpunere a nformaţiei:
Prezent cuv prin litere şi cifre;
Prezent melodiei prin note muzicale;
Prezentarea cifrelor sistemului zecimal prin cifrele sistemului binar de numeraţie; etc.
Def: procesul de reformare a modului de prezentare a informaţiei se numeşte codificare. Codificarea a aparut iniţial ca o necesitate de a transmite mesaje într-o formă cifrată formă ce poate deveni inteligibilă numai pentru cel ce cunoaşte cheea codificăr. Acestea st situaţii specifice a manipulări unor informaţii secrete sau confidenţiale.
Fie A={a0,a1,..., am-1 } mulţmea simbolurlor primare emise de o sursă de nformaţie şi care urmează a fi codificată prn intermediul unor simboluri elementare dintr-o altă mulţime B={b0, b1,..., bn-1 }. Prin operaţa de codificare se asociază fiecărui element aiA al sursei primare de informaţie, o secvenţă de simboluri biB, astfel încît modelul de codificare va fi reprezentat printr-o corespondenţă biunivocă. Prin S=s0, s1, ..., sm-1 notăm mulţimea cuvintelor de cod. Def: codul format doar dn cifre se numeşte cod numeric,iar codul format din cifre si litere se numeşte cod alfanumeric.
În tehnica de calcul se utilzează sistemul binar de numeraţie =0, 1 care stă la baza principiului de lucru al circuitelor integrate. Prin urmare orice informaţie în tehnica de calcul este prezentată prin coduri compuse din 0 şi 1.
Coduri numerce st utilizate pentru prezentare marimilor unipolare şi bipolare. Cod.numerice pot fi ponderate şi neponderate.
Coduri unipolare ponderate(CUP). Pt prezentarea mărimilor pozitive se utilzeazăp următoarele CUP:
1 codul binar natural (CBN)
2 coduri ponderate zecimal – binare.(CZB)
CBN este cel ma utlizat cod. Prin CBN pot fi prezentate atît numerele întreg cît ş numerele subunitare.un cuvînt de cod în CBN este identic cu numărul respectiv în sistemul binar de numeraţie. Numărul zecimal prezentat în CBN poate fi calculat prin adunarea ponderilor rangurilor diferite de zero:
Ex:110,12=1*22+1*21+0*20+1*2-1=4+2+0+1/2=6,510
CZB. În această clasă de CZB mulţimea A a sursei primare de informaţie supusă codifcări este A=0,1,2,3
4,5,6,7,8,9, iar multmea S a cuvintelor de cod trebue să conţină cel putin 10 cuvinte distincte. Cele mai utilzate CZB st: 8421, 2421, 4221, 7421.
Coduri bipolare ponderate. Pt prezentarea în tehnica de calcul a mărimilor bipolare se utilizează următoarele coduri bipolare ponderate: direct, invers, complementar, deplasat.
Codul drect. În codul direct pt numerele pozitive şi negative egale după valoarea absolută valorilor tuturor rangurilor coincid, cu excepţia rahgului de popularitate cae este egal cu „0” pt numerele pozitive şi egal cu „1” pt numerele negative.
Codul invers este supranumit şi complement faţă de 1 sau pomplement logic. Codul invers al unui numar pozitiv coicide cu codul direct. Număruul negativ în codul invers se obţine prin înlocuirea tuturor cifrelor „0” prin „1” şi „1” prin „0” în reprezentarea binară a numărului pozitiv.
Def: inversul unui numr negativ se obţine prin inversarea tuturor cifrelor şi ataşarea cifrei 1 în rangul semn.
Cifra „0” în codul invers are 2 reprezentări:a) „0”pozitiv (+0in)=0..0; b) „0”negativ (-0in)=1..1.
Utilizatea codului invers simplifică considerabil efectuarea unor operaţii logice deoarece transformarea tuturor cifrelor „1” în „0” sau invers coincide cu operaţia logică de negativare.
Codul complementar este supranumit şi complement faţă de 2 sau complement aritmetic.
Def: complemetul unui număr negativ se obţine prin inversarea tuturor cifrelor, sumîndu – se 1 la LSB, cifra semn fiind 1.
De ex.: N = -1010,11012; Nc=10101,0010+0,0001=10101,00112
Prin utilizarea codului complementar operaţia de scădere a 2 numere pozitive este înlocuită prin adunarea codului complementar al descăzutului pentru care Nc=2n+1+N.
Coduri alfanumerice: codurile alfanumerice în tehnica d eclaculstabilesc o corespondenţă biunivocă întrre
mulţimeasa caracterelor textuale (ltere, cfre, semne speciale) s= (a, b, ..., z. A, B, ...,Z, 0,1, ..., +, ..., &) şi mulţmea cuvintelor binare de cod de o lungime anumită.
P-u codificarea acestor caractere, standardele internaţionale impun o serie de restricţii. După cum se va observa, aceste restricţ st benefce p-u prelucrarea caracterelor. Să considerăm mulţimili: l – mulţimea literelor mic ale alfabetului latin, L – mulţimea literelor mari, c – mulţimea cifrelor zecmale, s – mulţimea caracterelor speciale (spaţiul l vom nota cu ), iar f – multimea caraterelor funcţionale, cele care nbu apar la listare (afişare) c doar dirjează listarea.deci: l= a, b,...,z; L=A,B,..,Z; c=0,1,...9; s= , +,*,...,;,:,%; f=CR, LF, TAB, BEL, ....
Un prm sistem de codifcare stabilt a ft EBCDIC (Extended Bnary Decimal Interchange Code), care codifcă în intervalul [0, 255]. Această codificare s-a menţnut la calculatoarele medi / mari (mai ales la familia IBM).
Prin codificarea EBCDIC se asociază fiecărui caracter o succesune de 8 cifre binare (8biti), astfel ca la 2 caractere dstincte să corespundă 2 coduri distincte. Cu 8 biti se pot reprezenta 28=256 caractere, dar st utilizate doar 106 combinaţii.
În prezent cel mai folosit este ASCII (American Standard Code for Information Interchange), deoarece el a ft adoptat p-u calculatoare personale. Acesta este un cod de 7 biţi, deci valorile codurilor pot fi în intervalul[0, 127].
El are în plus o serie de calităţ dntre care:
Codurile literelor mari şi mci st succesive, adică: C( z)= C( a)+25 sau C( Z)= C( A)+25
Trecerea de la ltere mari la litere mici se realizeaz simplu
Este simplă trecerea de la codificar5ea sirurilor de caractere la coduş BCD;
Bitul cel mai semnficativ nefiind utlizat se consideră implicit 0.
6 |
Reprezent nr în tehnica de calcul. Reprezent nr întregi fără semn. Reprezent nr fracționare fără semn. |
În tehnica de clacul se utilizează în special sistemul vinar de numeraţie să coduri construite în baza acestui sistem. Reprezentarea numerelor se face, d regulă, pe un număr întreg de octeţi (8 biti formează 1 octet sau byte). Numerele reprezentate în forma binară se păstrează în registri compuse din circuie bistabile.
Def: definim prin registru un dispozitiv electronic numeric compus din bistabili şi dedtinat memorări numerlelor binare, iar prin circut bistabil un dispozitiv electronic cu 2 stări stabile destinat memorării unei cifre binare.
În tehnica de calcul deosebim modurile de reprezentare a numerelor:
Reprezentarea nr întregi fara semn
Reprezent nr fractionare fără semn
Reprezent nr cu semn şi virgulă fiză
Reprezentarea nr în virgulă flotantă.
Reprezentarea numerelor întregi fara semn. Numerele întregi pozitive se reprezinta natural, memorând expresia lor în baza doi, într-un numar predeterminat de pozitii binare. Întrucât byte-ul este unitatea de adresare, se folosesc doar multipli de 8 biti pentru reprezentare, usurând operatiile de transfer între microprocesor si UM. De exemplu, daca se foloseste un byte, numarul întreg 36 va avea urmatoarea reprezentare :
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
întrucât 3610=1001002
Se observa ca pozitiile suplimentare au fost completat cu zerouri.
Acelasi numar s-ar reprezenta pe 16 de biti astfel :
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
adica pur si simplu se mai adauga opt de zero la început.
Reprezntarea numerelor fractionare fără semn. La fel ca si munerele întregi fără semn, numerele fractionare binare fără semn pot fi reprezentate printr-un cod binar. În această convenţie se operează numai cu numere pozitie.
Ex. Reprezentarea nr binar fractonar 1110,0112 = 30,37510 într-un registru de 8 biti
7 6 5 4 3 2 1 0 Rang
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
MSB LSB
Punctul zecimal nu se reprezintă fizic în registru sau locaie de memorie, el fiind fixat implicit, de unde şi determinarea de reprezntare în virgulă fixă.
7 |
Reprezentarea numerelor cu virgule flotantă. Reprezentarea numerelor în simplă precizie. Reprezentarea numerelor în dublă precizie. Reprezentarea numerelor în quadruplă precizie. Standard populare de reprezentare a numerelor. |
Acest mod de reprezentare a numerelor este utilizat în tehnica de calcul cu scopul înlăturării neajunsurilor legate de depăşirile aritmetice şi nearitmetice. Sarcina gestiunii virgulei zecimale p-t modul de reprezentare a numerelor în virgulă flotantă revine sistemului de calcul.
Se stie că orice număr real N, daca N≠0, se paote scrie în sistemul binar de numeraţie astfel
N=1,M*2E, (1)
Unde M poarta numele de mantisă, E exponent , M şi E fiind scrise în baza 2. Acestui mod de scriere ii spune scriere cu mantisă supraunitară.
Numerele reprezentate sub forma (1) se spune că st reprezentate în virgulă flotantă sau virgulă mbilă.
Fie reprezentarea unui număr în virgulă flotantă pe 4 octeţi:
31 30 (e) 24 23 22 (m) 0 Rang
SE |
E |
SM |
M |
Conform figurii în locatia de memorie st 4 zone:
Zona SE de 1 bit reine bitul de semn al exponentului
Zona E pe e biti reţine cifrele exponentului
Zona SM de 1 bit reţine bitul de semn al mantisei
Zona M pe m bii reţine cifrele mantisei.
Dacă n este dimentsiunea locaţiei de reprezntare, atunci p-u n obinem n=2+m+e.
Regulile de convertire a unuinumăr zecimal într-un număr binar în virgulă flotantă st:
Se converteşte nr zecimal în nr binar, conform regulii de convertire a unui nr mixt şi se reprezintă nr în cod complementa;
Se aduce mantisa la forma normalizată, adică mantisa trebuie să aparţină intervalului [1/2,1); pt ac4easta daca nr este supraunitar se vor executa deplasări la dreapta şi se4 adunăm cîte un unu şa exponent, reprezentat şi el sub forma binară, dacvă este subunitar se execută deplasări la stînga şi se scade cîte un unu din exponent;
Se determină caacteristica numărului.
Astfel, (ex.)nr 33,510 se converteşte în virgulă flotantă in modul următor:
Se converteşte în binar şi ffind pozitiv coincide cu codul complementar, adică 100001,12;
Se normalizează obţinînd: M=0,10000112 şi E=1102;
Considerînd Q= 12810= 10000002, se obţine C=Q+E=1000110.
Se poate observa, ca regulile de conversie inversă, din binar virgulă flotantă în zecimal, st următoarele:
Se converteşte mantisa în nr binar corespunzător (fiind considerată în cod complementar) şi se pune eventual semnul în faţă;
Se converteşte caacteristica în exponent;âse consideră virgula zecimală între semn şi prima cifră;
Se mută virgula zecimală la dreapta cu atîtea pozitii cît este valoarea exponentului, dacă acesta este pozitiv şi respetiv la stînga dacă este negativ;
Nr astfel obţinut se converteşte în baza 10.
8 |
Principiile clasificării calculatoarelor electronice. Clasificarea calculatoarelor după L.N. Koroliov. |
După destinaţie:
Calculatoare universale - destnate p-ru reyolvarea unui cerc larg de problem din diferite domenii
Calculatoare special – destinate p-ru reyolvareaunui cerc îngust de probleme sau numai a uneia.
După principiu de lucru:
Calculatoare analogice – operează cu informaţia prezentată în mod continuu. Fiecărei valori momentane aunei mărimi matematice îi corespunde o valoare momentană a mărimii fizice.
Calculatoare discrete (numerice) prelucrează informaţia în mod discret în formă de şir de numere codificate
Calculatoare combinate (numerico-analoage) prelucrează informaţia în mod discret şi în mod continuu
CLASIFICAREA CALCULATORELOR DUPĂ L. N. KOROLIOV
Calculatoare universale – primele au apărut calculatoarele universale denumte şi super calculatoare universale, baza elementală a căror a parcurs de la tuburi electronice pînă la circuite integrate. Un supercalculator universal (mainframe) reprezintă un sistem multiutilizator de calcul cu cele mai performanţe posibile, proiectat p-ru a satisface cerinţele de lucru pe calculator la organizaţii mari, ele lucrează în regim de partajare a timpului între mai mulţi utilizatori.
Minicalculatoare - Apariţia a fost cauzată de progresul obţinut în dezvoltarea bazei elemntare şi excedenţa resurselor supercalculatoarelor universale pt deservirea unui şir de aplicaţii. Minicalculatoarele sunt utilizate în regim de partajare a timpului p-ru dirijarea cu procesele tehnologice, drept ssteme de prelucrare a datelor şi noduri în reţele de calculatoare, p-ru schimbul de informaţie pe liniile de comunicaţie. Minicalculatoarele au o productivitate joasă în comparaţie cu supercalculatoarele universale.
Microcalculatoarele se împart în: Microcalculatoare multiutilizator care lucrează în regim de partajare a timpului
Staţii automatizate de lucru reprezintă microcalculatoare completate cu toate mijloacele necesare pentru îndeplinirea unor lucrări specifice. Termenul de staţie automatizată (workstation) este des utilizat de reţelele de calculatoare
Microcalculatoare încorporate mijloace de calcul utilizate p-ru dirijarea şi prelucrarea datelor în regim de timp real.
Calculatorul personal (PC)- microcalculator universal monoutilizator, sunt utilizate-ru rezolvarea unui set larg de probleme din diferite domenii.
Calculatoare aritmetice reprezintă o maşină electronică de calcul care după posibilităţile ei este aproximativ echivlentă cu rigla logaritmică. Se deosebesc: calc. aritmetice programabile care efectuează calcule conform programului introdus de la tastatură şi calc. aritmetice neprogramabile care efectuează calcule conform indicaţiilor utilizatorului prin apăsarea tastelor de comandă.
GENERAŢII DE CALCULATOARE:
Prima generaţie (1946-1956) cuprinde calculatoarele cu tuburi electronice;
A doua generaţie (1957-1963) include calculatoarele realizate în principal pe tranzistori;
A treia generaţie de calculatoare(1964-1981) include calculatoarele care au la bază circuite integrat;
A patra generaţie de calculatoare au început să se producă începînd cu 1982, odată cu dezvoltarea microprocesorelor (Apple).
În anul 1981 la Tokio a fost propusă organizarea calculatoarelor de generaţia a cincea care aveau o structurăradical modificată. O nouă organizare a memoriei interne, noi limbaje de programare.
9 |
Operatii logice. Familii de f.l. fundamentale echivalente |
Pt descrierea principiului de lucru a DN se utiliz argument, functii logice.
Var/arg–semnale aplicate la DN. Marime care poate avea 2 valori: DA/NU; 1/0; a,b,c,d…z; xn-1,xn-2…x1,x0
Functii – semnale obtinute la ies din DN. Poate avea numai 2 valori. Daca functia obtinuta se aplica la alte DN, atunci ea e argument pt urm DN. Se noteaza: f(a,b,c…z); f(xn-1,xn-2…x1,x0).
Pt descrierea principiului de lucru a DN, se utiliz 3 functii logice elimentare: NU, SI, SAU.
NU – f cu 1 argum, prez oper de negare:
SI – f de 2..n argum, 1 – toti1; 0 – macar 1 = 0:
Ca circuit electric, poate fi reprez prin comutoare legate consecutiv:
![]()
SAU – f de 2..n arg, 1-macar1=1, 0-toti=0. Poate fi prez ca conexiune paralela a comutoarelor:
![]()
AXIOMELE ŞI TEOREMELE DE BAZĂ A ALGEBREI LOGICE
AXIOME
NU → x=x=;
SI →x*0=0; x*1=x; x*x-=0; x*x…x=x;
SAU →x+0=x; x+1=1; x+x–=1; x+x=x.
TEOREME
Comutativa: a+b=b+a;
Asociativa – argum pot fi grupati: a+b+c=(a+b)+c=a+(b+c);
Distributiva – pot fi deschise parantezele intr-o prezentare algebric a f: a(b+c)=ab+ac;
Asimilarii/alipirii - in prezentari alg.logic, nr de argum pot fi micsorat: a+ab=a(1+b)=a;
De Morgan – valabila pt f cu 2..n argum:
∑ inversa al arg e egala cu ∏ arg negate;
∏ inversat al arg e egal cu ∑ arg negate.
FAMILII DE F.L. FUNDAMENTALE
Posibilitatea de a inlocuit familia de functii fundamentale prin: SI-NU; SAU-NU.
Familia de f.l. reprez f.l. fundamentale echivalente. Orice DN poate fi construit in baza unei familii de f.l. A.L.≈80 familii de f.l.
SI-NU – f.l. de 2..n arg, 0:toti=1, 1:1=0;
SI-NU, prin asa conex inteplineste f NU:
SI-NU, prin asa conex inteplineste f SI:
SI-NU, prin asa conex inteplineste f SAU:
SAU-NU - f.l. de 2..n arg, 1:toti=0, 0:1=1;
10 |
Metodele de prezentare ale funcțiilor logice. Minimizarea funcțiilor logice. Definirea mintermenilor, maxtermenilor. |
METODE DE PREZENTARE A F.L.:
Scriptica – depunerea sarcinii pt proiectarea DN
Tabele de adevar - se elab in baza formei scriptice, care arata toate starile posib a DN. Reprez un table in care sunt toate combinatiile posibile ale argum si valorile functiei.
Met. algebrica – in baza tabelului starilor poate fi obtinuta relatia matematica. Poate fi prez in 2 forme:
FCND – exp logica prezinta suma minterm - produs logic al argum, luati cite 1 in stare directa/inversa. Din ea se obtine FCNC.
FCNC – expresie logicacare prezinta produsul maxtermenilor – suma logica a argum luati cite 1 in stare directa/inversa
Numerica – se utiliz pt a prescurta scrierea F.L.
FCND: f(a,b,c)=∑(minterm(1));
FCNC: f(a,b,c)=∏(maxterm(1)).
Schema electrica
Etapele procesului de proiect a dn:
Determin sarcinilor, functiilor;
Completarea tabelelor starilor;
Scrierea FCND/FCNC;
Minimizarea f.l.;
Desenarea schemelor electrice.
PROCESUL DE MINIMIZE A F.L. duce la simplificarea prezentarilor acestor functii.
Avantaje:
Se micsoreaza nr de elem a D;
Se mareste viteza de lucru;
Se micsoreaza consumul de energie;
Se micsoreaza gabariturile;
Se micsoreaza costul.
Procedura de minimize e obligatorie in procesul proiectarii DN.
Metode de efectuare a minimiz:
Algebrica – se aplica teoreme, axiomele;
Cuburilor
Karnaugh – utiliz tabelelor de minterm
Proprietatile tabelelor de minterm:
Minterm plasati pe celulele vecine pe coloane/rinduri, se deosebesc cu o stare;
Minterm plasati la frontier tabelului se deosebesc printr-o singura stare;
M.Vecini – se deosebesc cu o sing stare;
M.Vecini pot fi grupati cite 1,2,4… (2n);
In grupul form nu trebuie sa fie minterm cu valoarea 0.
Exe procesului de minimiz:
Se introduce minterm = 1 in T.Karnaugh;
Se form grupuri de minterm;
Nr. minterm intr-un grup sa fie cit mai >;
Minterm dintr-un grup pot fi utilize si in alte grupuri;
Pt fiecare grup se scrie relatia simplific in modul urm:
Daca argum respectiv, in grupul dat isi schimba valoarea, el nu se scrie;
Daca nu-si schimba valoarea, se scrie cu valoarea sa.
Minimiz funct nedefinite complet – f.l. pt care unele stari la ies DN pot fi 0/1 si nu afecteaza lucrul DN.
ex: f(a,b,c,d)=∑(0,1,2,4,5,6,8,9~,10~,12~)
daca in table sunt mai multe unitati, atunci adaugam 1 in loc de minterm cu ~.
11 |
Definirea bistabilului. Bistabili cu o treaptă RS-asincron, RS-sincron și de tip D. |
Bistabil – dispoz electronic logic, care se poate afla in 2 stari stabile. Se utiliz pt inscrierea, pastrarea, prezentarea inf.
Clasificare:
cu 1 treapta: RS-sincron, RS-asincron, D – pot inscrie, pastra, prezenta un bit de inf;
cu 2 trepte: MS, DV, T, JK – pot opera cu 2 biti de inf.
RS-asincron – Nu se utilizeaza in practica, dar sta la baza tuturor bistabilelor.
B construit din elem:
SAU-NU

S – set (inscrierea, instalarea, introducerea);
R – reset (instalarea in starea initiala);
Q, Q – ies cu stare directa / inversa a inf.
Q=R+Q , Q=S+Q

S=0, R=0, Q=0+Q=Q=Q, Q=0+Q=Q;
S=0, R=1, Q=1+Q=1=0, Q=0+0=1;
S=1, R=0, Q=1+Q=1=0, Q=0+0=1;
S=1, R=1, Q=1+Q=1=0, Q=1+Q=1=0.
SI-NU

Q=S*Q, Q=R*Q

S=0, R=0, Q=Q, Q=Q;
S=0, R=1, Q=1, Q=0;
S=1, R=0, Q=1, Q=1;
S=1, R=1, Q=1, Q=1.
Neajunsuri:
Starea RS=11 interzisa
Dupa inscrierea inf noi – veche se pierde;
Nu are canal de dirijare, nu poate fi sincronizat cu procesul de lucru a prog.
RS-sincon construit din SI-NU:
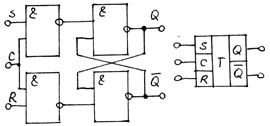
Q=C*S*Q, Q=C*R*Q

C=0, S=1, R=1, Q=Q, Q=Q;
C=1, S=0, R=0, Q=Q, Q=Q;
C=1, S=0, R=1, Q=1, Q=0;
C=1, S=1, R=0, Q=1, Q=0;
C=1, S=1, R=1, Q=1, Q=1;
Dezavantaje:
Starea RS=11 e interzisa;
Dupa inscrierea inf noi – veche se pierde.
Avantaj: are canal de dirijare.
D - fizic inlatura starea RS=11.

Q=C*D*Q, Q=C*C*D=Q
C=0 – deconect, C=1 – conect.

12 |
Definirea bistabilului. Bistabili cu două trepre MS, DV, T și JK. |
Bistabil – dispoz electronic logic, care se poate afla in 2 stari stabile. Se utiliz pt inscrierea, pastrarea, prezentarea inf.
Clasificare:
cu 1 treapta: RS-sincron, RS-asincron, D – pot inscrie, pastra, prezenta un bit de inf;
cu 2 trepte: MS, DV, T, JK – pot opera cu 2 biti de inf.
MS – construit pe baza RS-sincron.
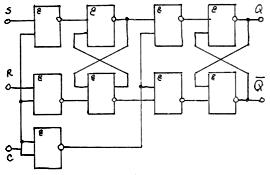
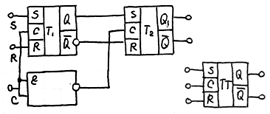
Prima treapta isi schimba starea dupa aplicarea semnal C, iar 2 – semnal C.
C–consecutivit impulsurilor dreptunghiulare
1–front anterior,
2 – front posterior.
Starea bistab se schimba dupa aplicarea 1.
Diagrama Temporala – grafic care arata cum se schimba semnalul in timp.
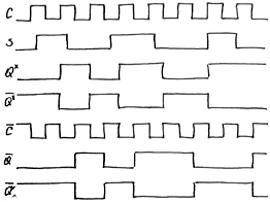
Din DT se observa:
Starea treptei 2 se schimba cu intirziere de jum de perioada, in comparative cu 1.
In bistab exista interval de timp cind se pastreaza si inf noua si veche (Q*=0, Q=1).
Neajuns: RS=11 – interzis.
DV – se utilize pt a evitat starea RS=11. DV exclude fizic aplicarea starii 11.
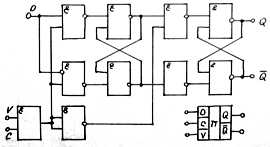
Regimuri de lucru:
Daca V=0 – semnalul de tactare nu trece. In acest caz, indifferent de D, starea bistab nu se schimba. Reprezinta regimul de pastrare a inf, pe orice timp.
V=1 – trece semnalul de tactare. Starea bistab depinde de D.
T – se utilize ca divisor de fregventa, dar nu pt crearea memoriei.
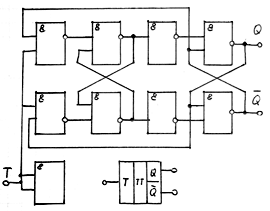
S – e connect cu circuitul de reactive Q, R-Q
JK – construiti pe baza bistab MS/Univers

Tab de adevar pt toate starile posibile:
![]()
B se utiliz pt construirea RG, Contoare.
13 |
Registru. Definiția. Registru paralel. Registru de deplasare direct. |
REGISTRU – dispoz electronic logic, construit din bistabili. Utiliz pt inscrierea, pastrarea, prezentarea unui cuv de inform.
Parametrii principali:
Ordenul – din citi bistabili e construit, arata de ce ordin poate fi inscris cuv;
Viteza de lucru (nr.oper/s) – depinde de fregventa de tactare maxim posibila;
Timpul de acces – interval de timp din momentul elaborarii cererii de catre microprocesor pe a primi inf, pina in mom afisarii inf de registru pe magistrala de date;
Energia consumata
Clasificarea R:
A: 1. Monofazati – la ies sunt numai stari dircte / numai stari inverse;
2. Bifazati – si stari directe si inverse.
B: Dupa modul de inscriere a inform:
Paralel
Consecutiv
Combinati
C: Dupa modul de prelucrare a inform:
De transformare a codului – pot transforma inf din cod consecutive in cod parallel si invers;
De deplasare a inform – permite deplasarea inf in interiorul registrului;
De inversare a codului – transforma din cod direct in cod incers.
REGISTRU PARALEL – inscrie, pastreaza, prezinta inf in cod paralel. Au cea mai mare viteza de lucru.
Cuv: A=an-1, an-2,…, a1, a0