1. Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця), він допускає операції (додавання, віднімання, множення тамноження на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В цій статті вони розглядатися не будуть.

Додавання[ред.]

Якщо дано дві матриці m-на-n A і B, можемо означити їх суму A + B як матрицю m-на-n, що утворюється додаванням відповідних елементів, себто, (A + B)[i, j] = A[i, j] + B[i, j]. Наприклад,

Множення на скаляр[ред.]

Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[i, j] = cA[i, j]. Наприклад,

З цими двома операціями множина M(m, n, R) усіх матриць m-на-n з дійсними елементами є дійсним векторним простором розмірності mn.

Множення матриць[ред.]

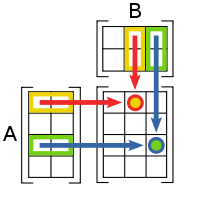
Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, n стовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, pстовпчиків), що розраховується за формулою:

(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.

Наприклад,

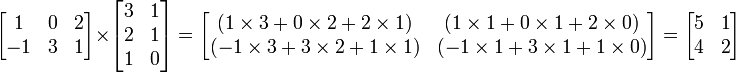
Це множення має такі властивості:

• (AB)C = A(BC) для всіх матриць A розмірності k-на-m, B розмірності m-на-n і C розмірності n-на-p (асоціативність).

• (A + B)C = AC + BC для всіх матриць A і B розмірності m-на-n і матриць C розмірності n-на-k (дистрибутивність).

• C(A + B) = CA + CB для всіх матриць A і B розмірності m-на-n і матриць C розмірності k-на-m (дистрибутивність).

Зауваження: комутативність має місце не завжди: для добутку певних матриць A і B може бути AB ≠ BA.

Матриці називають антикомутативними, якщо AB = −BA. Такі матриці є дуже важливими в представленнях алгебр Лі та в представленнях алгебр Кліффорда.

2. Ко́мпле́ксні чи́сла, — розширення поля дійсних чисел, зазвичай позначається  . Будь-яке комплексне число може бути представлене, як формальна сума  , де  і   — дійсні числа,   — уявна одиниця^[1].

Арифметичні дії виконуються аналогічно до дій з многочленами, але з урахуванням рівності  . Нехай   та   — комплексні числа. Тоді:

1. 

2. 

3. 

4. 

Для комплексних чисел певним чином визначають також інші операції, наприклад, піднесення до довільного комплексного степеня, логарифмування, знаходженнясинуса, косинуса тощо. Деякі з цих операцій не є однозначними і ведуть до розгляду багатозначних функцій, які взагалі часто виникають при вивченні функцій комплексної змінної. Теорію про функції комплексної змінної часто називають комплексним аналізом. Одним зі способів означення елементарних функцій комплексної змінної є задання такої функції як суми степеневого ряду, в який можна розкласти аналогічну функцію дійсної змінної (див. Ряд Тейлора).

Зв'язані визначення[ред.]

Нехай   і   — дійсні числа, такі, що комплексне число   (звичайні позначення). Тоді

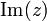• Числа   і   називаються відповідно дійсною (Real) і уявною (Imaginary) частинами  .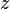

  • Якщо 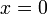 , то   називається уявним або чисто уявним.

• Число 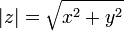  називається модулем числа  . Для дійсного числа модуль збігається з його абсолютною величиною. Деякі властивості модуля:

, причому   тоді і тільки тоді, коли 

 (нерівність трикутника)

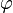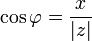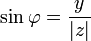• Кут   такий, що:   і  , називається аргументом  . Для комплексного нуля значення аргумента не визначене, для ненульового числа  аргумент визначається з точністю до 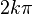 , де 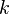  — будь-яке ціле число.

Спряжені числа[ред.]

Докладніше: Спряжені числа

Якщо комплексне число  , то число   називається спряженим (або комплексно спряженим) до  .

Перехід до спряженого числа можна розглядати як одномісну операцію; перерахуємо її властивості.

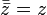•  (спряжене до спряженого є початкове)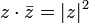

• 

• 

• 

• 

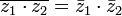
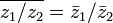
Узагальнення:  , де   — довільний комплексний многочлен.

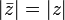•  (модуль спряженого числа такий же, як у вихідного)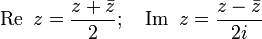

• 

3. Похідна́ — основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границявідношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційовною.

Похідна складеної функції

Нехай задано функції y=f(t) і t=g(x). Тепер підставимо другу функцію у першу.

Означення. Функція y=h(x)=f(g(x)) називається складеною функцією (суперпозицією або композицією) функцій відносно функцій f і g.

Наприклад, y=Sin²x – складена функція, бо вона є суперпозицією функцій y=u²; та u=Sin x.

Формула для знаходження похідної складеної функції записується так: (f(g(x)))'=f '(g(x))·g'(x).

4. Система рівнянь — набір двох і більше рівнянь, заданих функціями багатьох змінних, які повинні задовольнятися одночасно. Систему рівнянь можна записати в загальному вигляді:

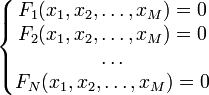
У загальному випадку система m лінійних рівнянь з n невідомими x1 x2 xn має слідуючий вигляд:

 

Числа aij називають  коефіцієнтами системи, а числа bi --  вільними членами системи.

Означення 1.  Розв'язком системи лінійних рівнянь називається упорядкована сукупність чисел  1 2 n (тобто, вектор), яка при підстановці замість невідомих перетворює кожне рівняння системи в тотожність.

Означення 2.  Система лінійних рівнянь, яка має хоч один розв'язок, називається сумісною. Якщо система не має розв'язків, то вона називається несумісною.

Означення 3.  Якщо сумісна система має лише один розв'язок, то її називають визначеною; в іншому випадку сумісну систему називають невизначеною.

Означення 4.  Дві системи називаються рівносильними або еквівалентними, якщо вони мають одну і ту ж множину розв'язків.

Означення 5.  Матрицю коефіцієнтів системи лінійних рівнянь називають основною матрицею або, просто, матрицею системи.

Систему лінійних рівнянь перепишемо у вигляді: або скорочено: AX=B. У такому випадку кажуть, що систему лінійних рівнянь записано у матричному вигляді.

Означення 6.  Матрицю складену з усіх коефіцієнтів при невідомих і вільних членах називають розширеною матрицею системи і позначають:

Означення 7.  Елементарними перетвореннями системи лінійних рівнянь назвемо такі перетворення, які не змінюють її розв'язку.

Легко бачити, що слідуючі перетворення системи є елементарними: (1) переставлення рівнянь місцями;

(2) множення рівняння на довільне число, відмінного від нуля;

(3) додавання до якогось рівняння іншого рівняння системи, помноженого на деяке число, відмінного від нуля.

Для розв'язку систем лінійних рівнянь застосовується метод Гаусса. Опишемо цей метод. Спочатку зведемо розширену матрицю системи до східчастого виду. Нехай у матриці східчастого виду r ненульових рядків. Якщо в останньому ненульовому рядку всі елементи дорівнюють нулю, крім елемента з стовпця вільних членів, то система несумісна. Інакше, нехай перші ненульові коефіцієнти ненульових рядків матриці східчастого виду розташовані в стовпцях з номерами k1 kr. Тоді невідомі xk1 xkr називатимемо  головними, а усі інші -  вільними. Очевидно, кількість вільних невідомих дорівнює n−r. З матриці східчастого виду одержимо систему r рівняннь з n невідомими. Дістанемо вирази головних невўіомих через вільні. Ці вирази називаються загальним розв'язком системи.

Надаючи вільним невідомим довільних числових значень, будемо одержувати  частинні розв'язки системи.

Теорема 8.  (Критерій сумісності Кронекера - Капеллі).Для сумісності системи лінійних рівняннь необхідно і достатньо, щоб ранг основної матриці системи дорівнював рангу розширеної матриці.

Означення 9.  Спільне значення рангів основної і розширенної матриць називають рангом сумісної системи лінійних рівняннь.

Наслідок 10.  (Критерій визначенності). Якщо ранг системи дорівнює кількості невідомих, то система визначена, якщо меньше - невизначена.    Розглянемо випадок, коли кількість рівнянь сумісної системи AX=B дорівнює кількості невідомих і дорівнює рангу системи. У цьому випадкуdetA =0. Тоді

AX=B X=A−1B

.

Означення 11.  Система лінійних рівнянь назив ається однорідною, якщо стовпець вільних членів складається з нулів (в іншому випадку -неоднорідною).

Легко бачити, що однорідна система завжди сумісна. Зауважимо, що нульовий вектор задовільняє рівняння усякої однорідної системи. Такий розв'язок однорідної системи називається  тривіальним.

Означення 12.  Фундаментальною системою розв'язків невизначенної однорідної системи лінійних рівнянь називається сукупність таких вектор-розв'язків, коли будь-який розв'язок однозначно зображається у вигляді лінійної комбінації вектор-розв'язків цієї сукупності.

Теорема 13.  Кількість вектор-розв'язків фундаментальною системою розв'язків однорідної системи лінійних рівнянь з n невідомими дорівнює n−r, де r - ранг системи.

Теорема 14.  Загальний розв'язок неоднорідної системи рівнянь дорівнює сумі частинного вектор-розв'язку цієї системи та загального вектор-розв'язку однорідної системи з тією ж матрицею коефіцієнтів.

5. Визначник або детермінант — вираз складений за певним законом з n² елементів квадратної матриці. Одна з найважливіших характеристик квадратних матриць.

Для квадратної матриці розміру   визначник є многочленом степеня   від елементів матриці, і є сумою добутків елементів матриці зі всіма можливими комбінаціями різних номерів рядків і стовпців (в кожному із добутків є рівно по одному елементу з кожного рядка і кожного стовпця). Кожному добутку приписується знак плюс чи мінус, в залежності від парності перестановкиномерів.

Якщо елементами матриці є числа, то визначник — також число. Взагалі, визначник може бути функціональним або належати якомусь комутативному кільцю, залежно від походження матриці.

З точністю до знака, визначник матриці виражає коефіціент, на який множаться  -мірні об'єми під дією цієї матриці.

Визначник матриці   задається формулою:

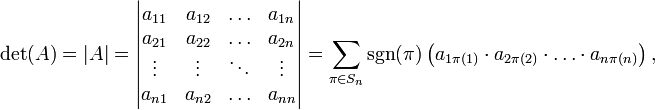
де   — перестановка множини   і   це знак (або парність) перестановки, тобто дорівнює 1 чи -1 залежно від парності числа інверсій 

Кількість доданків у сумі дорівнює   і номери рядка та стовпця елементів матриці, що входять у один добуток, не повторюються.

Матриця називається виродженою, якщо її визначник дорівнює нулю, а в іншому випадку невиродженою.

Визначник 2×2 матриці[ред.]

Щоб знайти визначник   матриці, множимо елементи головної діагоналі та віднімаємо добуток елементів побічної діагоналі:

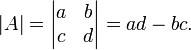
Визначник 3×3 матриці[ред.]

Щоб знайти визначник   матриці, будуємо шість добутків таким чином:

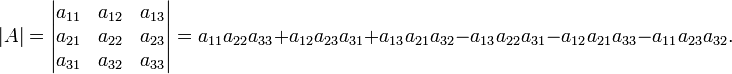
Для знаходження визначників високого порядку застосовуються принципово інші методи (насамперед, метод Гауса), що вимагають значно меншої кількості арифметичних операцій (  замість  ).

Властивості[ред.]

1. Якщо помножити якийсь рядок на константу 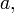  то визначник також помножиться на 

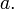
2. Якщо у матриці поміняти місцями будь-які два рядки, то знак визначника зміниться на протилежний.

3. При додаванні до будь-якого рядка лінійної комбінації кількох інших рядків визначник не зміниться.

4. У матриці з двома однаковими/пропорційними рядками або з нульовим рядком, визначник дорівнює нулю.

5. Всі властивості визначників, що стосуються рядків, так само справедливі і для стовпців.

6. Визначник трикутної матриці дорівнює добутку елементів на діагоналі.

7. Теорема Лапласа: визначник квадратної матриці дорівнює сумі добутків елементів деякого рядка на відповідні їм алгебраїчні доповнення.

8. Лема про фальшивий розклад: сума добутків елементів деякого рядка на алгебраїчні доповнення відповідних елементів паралельного рядка дорівнює нулю.

9. 

10. 

11. 

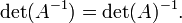
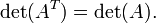
В лінійній алгебрі доводиться, що перші три властивості майже характеризують визначник матриць з елементами у полі. А саме, якщо функція елементів матриці задовільняє 1,2,3, то така функція пропорціональна  .

6. Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця), він допускає операції (додавання, віднімання, множення тамноження на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В цій статті вони розглядатися не будуть.

Мінор[ред.]

Визначник матриці, яка одержується з   викреслюванням всіх рядків та стовпців, окрім вибраних, називається мінором  -го порядку, розташованим в рядках з номерами   та стовпцях з номерами  .

Доповнювальний мінор[ред.]

Визначник матриці, яка одержується викреслюванням тільки вибраних рядків та стовпців з матриці   у випадку коли отримана матриця буде квадратною, називаєтьсядоповнювальним мінором до мінору 

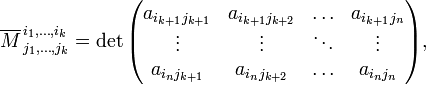
де   та   — номери не вибраних рядків і стовпців.

Мінор елемента[ред.]

Мінором   елемента   квадратної матриці   порядку   називається визначник (n-1) порядку, який одержуємо з визначника   n-го порядку шляхом викреслювання і-го рядка та j-го стовпця, на перетині яких знаходиться елемент 

Оточуючий мінор[ред.]

Нехай   — деякий мінор порядку   матриці  . Мінор порядку   матриці називається оточуючим для мінора  , якщо його матриця містить в собі матрицю мінору  . Таким чином, оточуючий мінор для мінора   можна одержати дописуючи нього один рядок і один стовпчик.

Базисний мінор[ред.]

Базисним мінором ненульової матриці   (існує ненульовий елемент) називається мінор, який не дорівнює нулю, а всі його оточуючі мінори дорівнюють нулю, або їх не існує.

Доведення існування базисного мінора: утворимо мінор з єдиного ненульового елемента і будемо рекурсивно шукати ненульові оточуючі мінори аж до найбільшого.

Зауваження. В загальному випадку в матриці може існувати багато базисних мінорів.

Розмір базисного мінора матриці називається рангом матриці.

Алгебраїчне доповнення мінора   визначається так:

де

 — доповнювальний мінор.

Алгебраїним доповненням елемента   називають мінор цього елемента, взятий зі знаком   тобто

Приклади[ред.]

• Мінор 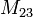  квадратної матриці   — визначник матриці, отриманий шляхом викреслювання рядка 2 та стовпчика 3:

   

• Знайти алгебраїчні доповнення елементів а₂₁ та а₃₃ визначника

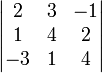
Розв'язок:

Алгебраїчні доповнення до елементів а₂₁ та а₃₃ позначимо А₂₁ та А₃₃, відповідно.

Знаходження мінорів:

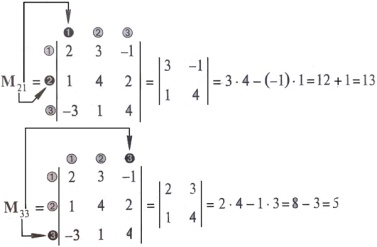
Підставимо ці значення мінорів у відповідні рівності (4), одержимо шукані алгебраїчні доповнення

А₂₁=(-1)²⁺¹ М₂₁= -13

А₃₃=(-1)³⁺³ М₃₃= 5