17) Чисельне інтегрування чисельне інтегрування Постановка задачі

Як відомо з курсу математичного аналізу, якщо на відрізку [a, b] функція 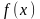неперервна та має первісну 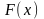, то визначений інтеграл від цієї функції в межах від a до b може бути обчислений за формулою Ньютона-Лейбніца:

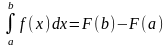, де

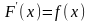
Але в багатьох випадках первісна функція не може бути знайдена за допомогою елементарних методів або є досить складною. Тому обчислення визначеного інтеграла за формулою Ньютона-Лейбніца може бути або занадто складним, або практично неможливим.

Крім того, в дослідженнях підінтегральна функція часто буває задана таблично, і тоді поняття первісної втрачає сенс. Аналогічні питання виникають і при обчисленні кратних інтегралів. Тому важливого значення набувають наближені чисельні методи обчислення визначених інтегралів.

Задача чисельного інтегрування функції полягає в обчисленні значення визначеного інтеграла на основі ряду значень підінтегральної функції.

Функцію , задану таблицею на відрізку [a, b], заміняють функцією більш простого вигляду (наприклад, поліномом), а потім наближено припускають

.

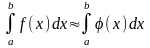Функція має бути такою, щоб інтеграл обчислювався безпосередньо простими засобами. Якщо функція задана аналітично, то додатково ставиться питання про оцінку похибки такого наближення.

Розглянемо більш детально застосування інтерполяційного полінома Лагранжа при наближеному інтегруванні.

Нехай для функці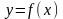ї в точках х₀, х₁, х₂, …. , х_п відрізка [a, b] відомі відповідні значення функції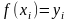 (і = 0, 1, 2, ... , п). Потрібно наближено знайти .

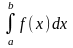За заданими значеннями у_і побудуємо поліном Лагранжа (див. роботу 4)

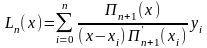, де .

Замінюючи функцію поліномом 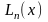, отримаємо рівність

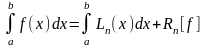(7.1)

де 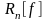– похибка квадратурної формули (залишковий член).

Звідси отримуємо наближену квадратурну формулу

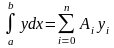, (7.2)

де

(і = 0, 1, 2, . . . , п).

Зазначимо, що коефіцієнти А_і при даному розміщенні вузлів не залежать від вигляду функції .

Якщо границі інтегрування a та b є вузлами інтерполяції, то квадратурна формула (7.2) називається формулою„замкнутого типу”, в протилежному випадку – „відкритого типу”.

Для полінома степеня п формула (7.2) точна, оскільки тоді 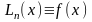; звідси слідує, що формула (7.2) точна при 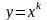(k = 0, 1, 2, . . . , п), тобто 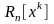= 0 при k = 0, 1, 2, . . . , п.

Зауважимо, що при застосуванні цього методу фактично побудова інтерполяційного полінома за методом Лагранжа не є потрібною. Цю побудову замінюють декількома спрощеними моделями, котрі разом з наочністю забезпечують потрібну точність обчислення.

13) Метод ітерацій та Зейделя

Застосування методу Гаусса для розв’язання системи лінійний рівнянь з великою кількістю невідомих досить громістке. В цих випадках краще використовувати ітераційні методи, тобто методи, які дозволяють будувати послідовність наближень, границя якої буде розв’язком системи лінійних рівнянь. Безумовно, що ця система повинна мати один, єдиний розв’язок.

Спочатку потрібно систему лінійних рівнянь подати у вигляді:

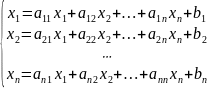(1)

Якщо виконується хоча б одна із умов 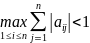, , 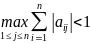, 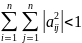то система рівнянь (1) має єдиний розв’язок, який є границею послідовності, що одержується методом простої ітерації або методом Зейделя.

Зауважимо, що систему n лінійних рівнянь з n невідомими, записану в традиційній звичній для нас формі, завжди можна подати у вигляді (1), причому так, щоб виконувалися умови збіжності. Наприклад, якщо модуль кожного діагонального елемента матриці системи більший від суми модулів інших елементів рядка, тобто

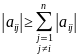, i=1,2,…,n (2)

то, розв’язавши перше рівняння відносно х₁, друге – відносно х₂ і т.д., дістанемо систему:

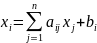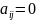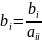, (i=1, 2, ..., n) , де , . При цьому буде виконуватися перша умова збіжності. Якщо ж система така, що умова (2) не виконується, то за допомогою елементарних перетворень системи можна домогтися її виконання.

Для розв’язання системи рівнянь методом простої ітерації за початкове наближення можна брати довільні значення коренів, наприклад, підставляти значення вільних членів (х1=b₁, х₂=b₂, ..., х_n=b_n). Підставляючи їх в праві частини системи (1), ми одержимо нові значення невідомих. Знову підставляємо одержані корені в праві частини системи (1), одержуючи нові значення невідомих і т.д. Цей процес продовжують до тих пір, поки не досягнуть бажаної точності.

Метод Зейделя відрізняється від методу простої ітерації тільки тим, що при обчисленні х_і на k-му кроці враховуються значення х₁, х₂, ..., х_k–1, обчислені не на попередньому а на цьому самому кроці. Завдяки тому, що значення цих коренів одержуються в якійсь мірі уточненими, метод Зейделя має кращу збіжність в порівнянні з методом простої ітерації.