30. Свойства вложений групп

Св-во: Пусть f:G₁→G₂ вложение. Тогда отображение f₁:G₁→Imf(Imf∙f(G₁)∙{f(g₁),g₁ G₁}. g₁ G₁ f₁(g₁)=f(g₁)-изоморфизм(G₁ Imf)

Док-во: Знаем, что если G₁ подгруппа G₂, то f(G₁<G₂) Imf<G₂

g₁ => f(g₁) => f₁(g₁) инъекция

g₂ Imf, значит g₁ G₁ f(g₁)=g₂, т.е. f₁(g₁)=g₂ –сюрьекция

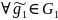g₁ , f₁( = f( = | f- гомоморфизм |= f(g₁)*f( )=f₁(g₁)* f₁( ) (по опред)

31, 32 Св-ва эпоморфизмов групп . Каноническое отображение группы на её фактор-группы. (Естественный гомоморфизм).

Св-во 12.10 <G₁, >— группа, N—нормальный делитель G. Тогда <G_/N, >— фактор-группа. Тогда отображение f:G→ G_/N; g → g N является эпиморфизмом и Kerf=N.

Док-во. f — задано. Докажем, что g₁ ,g₁~ f(g₁ g₁~)= f(g₁)  f(g₁~)=(g₁ g₁~) N.

f(g₁ g₁~)=(g₁ g₁~) N.

f(g₁)  f(g₁~)=(g₁ N)  (g₁~ N)= (g₁ g₁~) N.

Доказать Kerf=N

е N= N

е N={ е n/n N}={n/n N}=N

Доказать N Kerf

n N е^-1 n= n N е^—=n^— нейтральный в G_/N  е N= n  N f(n)= n N= n^—=е^— нейтральный в G_/N n Kerf

Докажем, что Kerf c N

Покажем, что x Kerff(x)=еNеN=xNе^—=x^—e~_Nxе^-1x Nx N Kerf c N.

Опр.12.11 f:G→ G_/N из св-ва 12.10 называется естественным гомоморфизмом группы G на фактор группе G_/N.

Св-во 12.12 Пусть дано <G₁,>; <G₂,*> и отображение

f: G₁G₂ —эпиморфизм у которого N= Kerf, то тогда G₁/N G_2.

Док-во. F: G₁/NG₂ : g₁ Nf(g₁). Покажем, что F это отображение. Т.е.результат действия F на смежные классы не зависит от того, через каких представителей записаны эти классы. Пусть g₁ N= g₁~ N. Тогда g₁^— = g₁~ g₁ ~_N g₁~ g₁^-1 g₁~ N  g₁^-1 g₁~= x Nf(g₁^-1 g₁~)=f(n) f(g₁)^-1 *f(g₁)=e₂ f(g₁~)=f(g₁). Покажем, что F — сюръективно. Возьмем g₂ G₂. Т.к.f— эпиморфизм g₁ G₁ , f(g₁)= g₂ , F(g₁ N)=g₂. Покажем, что F — инъекция. Пусть g₁ N g₁~ N, но F(g₁ N)= F(g₁~N)f(g₁)=f(g₁~) /* f(g₁^-1 )/  f(g₁^-1 )* f(g₁)= f(g₁^-1 )* f(g₁~) f(g₁^-1 g₁)= f(g₁^-1 g₁~)f(e₁)= f(g₁^-1 g₁~) e₂=f(g₁^-1 g₁~)g₁^-1 g₁~ Ker fg₁^-1 g₁~ g₁ ~_N g₁~ g₁^— =g₁^—~ g₁ N= g₁~ N — противоречие.

Докажем, что F — гомоморфизм. F((g₁ N)  (g₂ N))=F((g₁ g₂ ) N)=f(g₁)*f(g₂).

F(g₁ N)* F(g₂ N)= f(g₁)*f(g₂). Т.к.правые части равны, то левые тоже равны.

33.Теорема Лагранжа

Лемма: G-группа,Н-подгруппа ,тогда для любого g принадл. G отображение lg:H

является биекцией.Док-во: lg-отображение,инъекция; пусть h1 , lg(h1) (т.е не является инъекцией) g°h1= g°h2 тогда 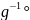g°h1=g^-1°g°h2 след-но h1= h2(противоречие);

lg-сюрьекция?для любого g°h принадлежит H, то lg(h)= g° h.

Опр. Если конечное множество и модуль G⁄H=k то число к –индекс подгруппы H в группе G.Обознач:[G:H]

Теорема Лагранжа: G-конечная группа, |G|=m, H⁄G, |H|= h, [G:H]=к,тогда |G|=|H|*[G:H] или m=n*k(порядок группы=произв. порядка подгруппы на ее индекс)

Док-во: т.к явл. отношением эквивалентности, при этом для любого g принадл. G, g с чертой= g°H, то левые смежные классы по подгруппе H задают разбиение множества G, т.е G= g1 °H

Модуль G=модуль g1 °H∪g2°H∪…∪gк°H отсюда |G|= |g1°H|+ |g2°H|+..+ |gк°H|,но по лемме gi°H = |H| след-но m=n+n+n+…+n(k-раз)

Следствие: m=n*k порядок подгруппы в конечной группе делит порядок подгруппы.