22. Нормальные делители группы. Операции со смежными классами по нормальному делителю. Корректность определения операции.

ОПРЕД.: Пусть <G;◦> - группа, x G, g G, тогда элемент g^-1◦x◦g называется элементом, сопряженным к элементу x (с пом. элемента x).

ОПРЕД.: Пусть <G;◦> - группа, подмножество N G называется нормальным делителем группы G или инвариантом подгруппы, если:

1. N<G

2. n N, g G g^-1◦n◦g N (обозначается N G)

СВОЙСТВО: <G;◦> - группа, N_i G, i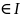 , тогда N= G

Д-во:1) N_i G (по условию) N_i G (из 1-го пункта определения)

2) (т.к. N_i G) , т.к. N G

ОПРЕД.: Пусть <G;◦> - группа, N G, g₁ G, g₂ G. Определим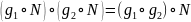 – правило умножения смежных классов по N.

Пример: / _͂4 ={0+4 , 1+4 , 2+4 , 3+4 }

4 , g^-1◦(4g₁)◦g=(-g)+4g₁+g=4g₁

ТЕОРЕМА: предыдущее определение корректно, т.е. результат операции над классами не зависит от того, через каких представителей записаны эти классы.

Д-во: 1 часть. Пусть .Доказать,

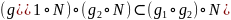
Причем слева – определение умножения класса или умножение двух множеств.

2 часть. Аналогично 1 части показываем

3 часть. _N

Однако, по условию

– истина.

23. Фактор-множество группы по нормальному делителю.

ТЕОРЕМА:Фактор-множество G/_N группы G по нормальному делителю N с введенной над ней операцией (правило умножения смежных классов по N) является группой.

Д-во: 1) ассоциативность

2)нейтральный в G/_N – это , т.е. нужно доказать, что

3)симметричный к - , т.е. нужно д-ть, что

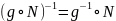
24. Гомоморфизмы групп. Определение, примеры, простейшие свойства.

ОПРЕД.: Пусть даны две группы <G₁;◦>, <G₂; >. Гомоморфизм из группы G₁ в G₂ – отображение f: , которое «сохраняет операцию», т.е.

ПРИМЕРЫ: 1) – мн-во невыраженных квадратных матриц размерности n x m, ;

, каждой матрице ставится в соответствие ее определитель.

Рассмотрим

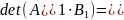– верно.

^{Умножение матриц умножение чисел}

2) Рассмотрим аддитивные группы и отображение

– истина.

3) , 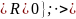зададим отображение

– истина.

СВОЙСТВО: При гомоморфизме образ нейтрального элемента является нейтральным. Т.е. (1)

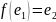
Д-во:

СВОЙСТВО: При гомоморфизме образ обратного элемента является обратным к образу данного. Т.е. если задан гомоморфизм (1), тогда

Д-во:

25. Гомоморфный образ подгруппы

ОПРЕД.: Пусть даны две группы <G₁;◦>, <G₂; >. Гомоморфизм из группы G₁ в G₂ – отображение f: , которое «сохраняет операцию», т.е.

Св-во. Гомоморфный образ подгруппы является подгруппой.

Док-во. Пусть дан гомоморфизм <G₁, >; <G₂,*> — группа. f: G₁ G₂ — гомоморфизм, то тогда

H₁<G₁f (H₁)<G₂. f (H₁)={f(h₁)/h₁ H₁}={h₂|h₂ H₂ сущ. h₁|h₁ H₁ и f(h₁)=h₂}. по критерию подгруппы f(H₁) содержит f(h₁) и f(H₁) f(h₁~)h₂^-1*h₂~ f(H₁)h₂^-1*h₂~ = =f(h₁)^-1*f(h₁~)=f(h₁^-1)*f(h₁~) =f(h₁^-1h₁~) f(H₁) По критерию подгруппы f(H₁)<G₂. Доказано.

26. Прообраз подгруппы при гомоморфизме

Св-во. Пусть дан гомоморфизм <G₁, >; <G₂,*> — группа. f: G₁ G₂ — гомоморфизм. H₂<G₂(f^-1(H₂)<G₁). При гомоморфизме полный прообраз подгруппы явл. подгруппой.

Док-во. f^-1(H₂)={h₁/h₁ G₁ и f(h₁) H₂} e₂ H₂ и f(e₁)=e₂ H₂e₁ f^-1(H₂)f^-1 (H₂)≠ø.

h₁ f^-1(H₂) и h₁~ f^-1(H₂)(h₁^-1h₁~) f^-1 (H₂)

f(h₁) H₂ и f(h₁) H₂(f(h₁)^-1)*f(h₁~) H₂f(h₁^-1)* f(h₁~) H₂f(h₁^-1  h₁~) H₂ (h₁^-1  h₁~) f^-1 (H₂) По критерию получим, что f^-1 (H₂)<G₁. Доказано.