8. Исключение ирр. В знаменателе(через минимальный многочлен)
Пусть
а – неприводимое иррациональное число.
,
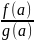где f(x)
Q[x],
g(x)
Q[x],
) g(x)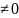
f-
алгебраический над Q.
p(x) Q[x] – минимальный многочлен а. Т.к. g(a) ) , то . Т.к. р(х) – неприводим, то р(х) и g(x)- взаимнопросты, НОД(р(х);g(x))=1. По критерию взаимной простоты u(x) Q[x], v(x) Q[x] такие,что u(x)g(x)+v(x)p(x)=1. Мы имеем алгебраическое равенство многочленов.
Подставим а.
u(а)g(а)+v(а)p(а)=1
0
g(a)u(a)=1
=>
=
=
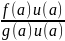=h(a)
;
h(x)=f(x)u(x) Q[x]
h(x) – не содержит иррациональных знаменателей, следовательно, мы решили задачу.
а/а-1=f(a)/g(a) p(x)= x3+x-3
найдем НОД(p(а) и g(a)). a3+а-3=(а-1) ∙ (а2+a+2)+1
x3+x-3=(x-1) ∙ (x2+x+2)+1
-1=(x-1) ∙ (x2+x+2)+(- x3-x+3), где последняя скобка = p(x)=0
т.к. имеет место алгебраическое равенство, то имеет равенство и функциональное
-1=(а-1) ∙ (а2+а+2) значит (а/(а-1)) ∙ (а-1) ∙ (а2+а+2)= а3+а+2=3-а+ а2+2а=3+ а+а2
9. Конечно порождённые расширения. Определения и строение.
Опр.5.1 Пусть заданы вложения полей Р с Т с F (1)’. Тогда (1) наз. цепочкой расширения.
P=P1 c P2 c…c Pz=F (1). Включения могут оказаться равенствами.
5.2 Пусть Р с F, z1, z2 F. Рассм. P1=P(z1)- простое расширение Р. Р1 с F, P1(z2)=P(z1)(z2).
Т 5.3 Пусть Р – подполе поля F. Z1, z2 F.
Р(z1)(z2)=
Док-во:
M
c
P(z1;z2)
;
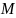; f(x;y)
f(x;y)
=
(x)
,
(z1)
g(x;y)
x=z1
f(z1;y)=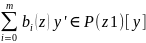
f(z1;z2)=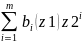
g(z1;z2)=
Возьмём
произвольный эл-т из P(z1)(z2)
t=
(*)
t
, все
Домножим
числитель и знаменатель на общий
знаменатель дробей, который получается
в результате сложения
Получим, что в числителе и знаменателе
из Р1=Р(z1)
на степени элементов z2
F2
По определению P[x;y]=P(x)(y)
Р(z1)
Св-во 5.4 Пусть Р – подполе F. Z1, z2 .
Тогда P(z1;z2)=P(z2;z1)
Док-во:
Р(z2;z1)=
Поэтому М=М1. Отсюда P(z1)(z2)=P(z2;z1). Это расширение обозначим P(z1;z2) и назавём расширением Р,с порождающими z1, z2.
Опр.
5.5.
Аналогично предыдущему, если дано
включение полей P
c
F,
z1,
z2
Рассм. P(z1,z2,….,zk),
кот. наз. Расширением поля P
c
конечным числом (сk)
пораждающих.
10. Алгебраические расширения.
Опр.6.1
Пусть Р с F
. Расширение F
наз. Алгебраическим расширением Р, если
Пр 6.2.1 R с C, z= a+bi; a, b R.
f(x)
=(x-(a+bi))(x-(a-bi))=((x-a)-bi)((x-a)+bi)=(x-a)2-(bi)2
=
x2-2ax+(a2+b2)
f(a+bi)=0
комплексное число явл. корнем многочлена с комплексными коэффициентами, значит
C является алгебраическим расширением R.
Пр.6.2.2 Q c Q[ ]
a+b
(x-(a+b
))(x+(a-b
))=((x-a)-b
)((x+a)+b
)=
(x-a)2-2b2=x2-2ax+(a2-2b2)
Т 6.3. конечное расширение явл. алгебраическим.
Д-во: Пусть дано P c F. [F:P]=n.
Возьмём
z
F,
(n+1)
эл-тов dim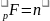
.
Значит 1,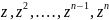
-
линейно зависим. над Р. Это значит
Т.е. произвольный эл-т из F является алгебраическим над Р, значит F- алгебраическое расширение Р.
Следствие6.4. Пусть дано расширение P c F, z F, z – алгебр. эл-т над P. => Р(z) - алгебраическое расширение Р.
Следствие6.5.
Р(z)
- алгебраическое расширение Р. Пусть z
– алгебр. эл-т над P
=>
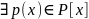такой, что р(х) – min
z.
В таком случае [P(z):P]=
deg
p(x)
Тогда по 6.4. расширение P(z) поля Р – конечно.
Св-во
6.6.
Пусть дано расширение P
c
F,
z1,z2
F,
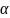– алгебр. эл-т над P,
a
z2
- алгебр. эл-т над P1=P1(z1).
Тогда z2-
алгебраичен над Р.
Док-во: P c P(z1) c P(z1)(z2) c F. z1 – алгебр. эл-т над P=> deg [P(z1):P] =m = deg p(x)
z2 – алгебр. эл-т над P1=> deg [P1(z2):P1] =k deg p1(x)
где р(х) – min эл-т z2 над Р1.
[P(z1)(z2):P]=
[P(z1)(z2):P(z1)]
P c P(z1)(z2) – его степень над Р =mk, т.е. она конечна, зн. она алгебр. над P. z2 этому расширению => z2- алгебр. над Р эл-т.