
- •1.1.Простое расширение поля.
- •4. Конечное расширение поля.
- •5. Минимальные алг. Элементов и их свойства
- •6. Степень и базис простого алгебраического расширения.
- •7. Исключение ирр. В знаменателе(через векторные пространства)
- •8. Исключение ирр. В знаменателе(через минимальный многочлен)
- •9. Конечно порождённые расширения. Определения и строение.
- •10. Алгебраические расширения.
- •11. Алгебраичность алгебраического расширения алгебраического расширения.
- •12. Поле алгебраических чисел.
- •13. Алгебраически замкнутые поля. Алгеброич. Замык. Поля рац.Чисел
- •14. Группы. Определение, прим., с-ва.
- •17. Подгруппы. Первый критерий подгруппы.
- •18. Подгруппы. Второй критерий подгруппы.
- •19. Подгруппы. Третий критерий подгруппы.
- •20. Отношение эквивалентности, задаваемое подгруппой на группе. Фактор-множество группы по подгруппе
- •21. Левые смежные классы элементов группы по подгруппе и классы эквивалентности.
- •22. Нормальные делители группы. Операции со смежными классами по нормальному делителю. Корректность определения операции.
- •23. Фактор-множество группы по нормальному делителю.
- •24. Гомоморфизмы групп. Определение, примеры, простейшие свойства.
- •25. Гомоморфный образ подгруппы
- •26. Прообраз подгруппы при гомоморфизме
- •27.Прообраз нормального делителя при гомоморфизме
- •28. Композиция гомоморфизмов
- •29.Изоморфизм групп. Определения, примеры, простейшие свойства.
- •30. Свойства вложений групп
- •33.Теорема Лагранжа
- •34.Группа подстановок
- •38. Циклические подгруппы и группы.
- •39. Кольца
- •40. Подкольца. Определение, примеры, простейшие свойства. Критерий подкольца.
- •41.Идеалы колец .Определение. Корректность определения.
- •42.Критерий идеала.
- •43.Операции с идеалом .Определение. Корректность определения.
- •45. Главные идеалы. Кольца главных идеалов. Определение и примеры.
- •46. Естесственный гомоморфизм кольца на его фактор-кольцо.
- •47. Максимальные идеалы. Фактор-кольцо по максимальному идеалу.
- •48. Простые идеалы. Фактор-кольцо по простому идеалу.
- •52 Теорема о примитивном элементе
- •53. Квадратичные расширения полей
1.Поле
Опр.
1.1
Пусть Х-непустое мн-во,будем говорить,что
на Х задана бинарная алг. Операция,если
для
 х,у
х,у Х
задан элемент х
Х
задан элемент х у
у
Опр.
1.2
Бинарная операция
на
мн. Х наз ассоциативной если
 ,
если опер. Ассоц,то <X,
>
наз. подгруппой
,
если опер. Ассоц,то <X,
>
наз. подгруппой
Опр.
1.3
Пусть на непустом мн М задана ассоц.опер.
,эл-т
 наз нейтральным,если
наз нейтральным,если
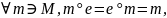 если
операция обозн. «+» и наз сложением,то
тогда эл-т е наз нулевым,если
операция обозн «
»
и на умнож. то нейтральный эл-т обычно
наз еденицей,если
в полугр. М есть нейтр. эл-т,то М наз
моноидом
если
операция обозн. «+» и наз сложением,то
тогда эл-т е наз нулевым,если
операция обозн «
»
и на умнож. то нейтральный эл-т обычно
наз еденицей,если
в полугр. М есть нейтр. эл-т,то М наз
моноидом
Опр.
1.4
если в моноиде <M,
>
для эл-та х ,то
эл-т у наз. симметричным
эл-ту х;если операция «+»,то эл-т у наз
противоположным
эл-ту х и обозн у=-х;если операция «
»и
наз умнож,то тогда у=х-1
наз обратным к х(х
,то
эл-т у наз. симметричным
эл-ту х;если операция «+»,то эл-т у наз
противоположным
эл-ту х и обозн у=-х;если операция «
»и
наз умнож,то тогда у=х-1
наз обратным к х(х )
)
Опр.1.5 Пусть <M, > монод и каждому эл-т из М-обратимый,т.e. к нему есть обратный,тогда М наз. группой
Опр.
1.6
Пусть на непустом мн К задана бинарная
алг.опер <K;+>-коммут.группа(аддитивная
тоже);<K;
>-полугруппа
и эти операц. связаны условием
дистрибутивности,т.е.
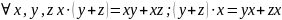 ,то
тогда К-наз кольцом
,то
тогда К-наз кольцом
Если операц. умнож в К-коммут,то кольцо К наз. коммут.Если в кольце К есть еденица,то кольцо К наз кольцом с еденицей
Опр.1.7 если в кольце К,кот комм.и с еденицей,у каждого ненулевого эл-та сущ обратный,то тогда К наз полем
Опр.
1.8
Пусть F-поле,PсF,кот
само явл полем относ операции слож и
умнож кот
 в F,тогда
говорят,что Р-подполе поля F
или,что F
явл расширением
поля Р
в F,тогда
говорят,что Р-подполе поля F
или,что F
явл расширением
поля Р
Опр.
1.9 Пусть
Р-некот.поле, V≠ зада бинарная опер слож на 0
зада бинарная опер слож на 0
 1)
слож
ассоц
1)
слож
ассоц

8)
 1
1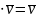
Слож коммут
 =
=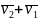 3)
3)
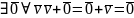 4)
4)
0)определено
умнож в скалярах(эл-тов из Р) на векторы
(эл-ты из Р) т.е.

5)
 6)
6)
7)

Тогда
говорят,что
 явл линейным(векторным)пространством
над Р
явл линейным(векторным)пространством
над Р
Опр. 1.10 Пусть F-поле,непустое подмножество Р наз подполем поля F,если само явл полем отномит тех операций которые сущ в F,в этом случае еще говорят,что F явл расширением поляР
2-3 Простое расширение поля.
Опр
2.1. Пусть Р-подполе в F,
РсА и z F.Будем
обозначать P(z)={
F.Будем
обозначать P(z)={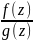 /
/
 }
}
Теор. 2.2 В условиях опр 2.1 Р(z) явл полем и это найм подполе а F,содержит Р и эл-т z
Опр 2.3 Р(z) наз простым расширением поля Р с помощью примитивного элемента z
Прим2.4
P=Q
F=К
z=
Q(
)={
/
 }
}
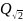 ={a+b
/a,b
Q}
Q
={a+b
/a,b
Q}
Q
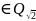 cQ
cQ f(x)=a+bx g(x)=1
f(x)=a+bx g(x)=1
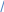
Ввиду
минимальности расширения
получаем
=Q
f(x)=x2-2
g(x)=1

Опр.
2.5 Пусть РсF,эл-т
z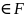 наз алгебраическим над Р,если сущ
многочлен f(x)
наз алгебраическим над Р,если сущ
многочлен f(x)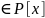 такой,что f(x)
такой,что f(x) 0
и при этом f(z)=0.Если
элемент z
не явл алгебраич над Р,то он наз
трансцендентным над Р
0
и при этом f(z)=0.Если
элемент z
не явл алгебраич над Р,то он наз
трансцендентным над Р
Опр.2.6 PcF. Расширение P(z) наз простым алг расширением,если эл-т z алгебр над Р и трансцинд,если z-трансцинд над Р
1.1.Простое расширение поля.
Пусть P[x] — кольцо полиномов от x над полем P, где P — подполе поля F. Напомним, что элемент a поля F называется алгебраическим над полем P, если a является корнем какого-нибудь полинома положительной степени из P [x].
Определение. Пусть P < F и a0F. Простым расширением поля P с помощью элемента a называется наименьшее подполе поля F, содержащее множество Р и элемент a. Простое расширение P с помощью a обозначается через P (a), основное множество поля P (a) обозначается через Р(a).
Пусть a0F, P [x] — кольцо полиномов от x и P[x]={f(a)*f0P[x]},т. е. P [a] есть множество всех выражений вида a0 + a1a+...+ anan, где а0, a1,...an0P и n — любое натуральное число.
Теорема 1.1. Пусть P [x]— кольцо полиномов от х над P и P (a)— простое расширение поля P. Пусть y — отображение P[x] на P[a] такое, что y(f)=f(a) для любого f из P[x]. Тогда:
(а) для любого а из Р y (а) = а; (b) y(x) = a; (с) y является гомоморфизмом кольца P [x] на кольцо P [a];
(d) Ker y ={f0P[x]*f(a)=0}; (е) фактор-кольцо P [x]/Кег y изоморфно кольцу P [a].
Доказательство. Утверждения (а) и (Ь) непосредственно следуют из определения y. Отображение y сохраняет главные операции кольца P [x], так как для любых f и g из P[x] y(f + g)=f(a)+g(a), y(fg)= f(a)g(a), y(1)=1.
Далее, по условию, y есть отображение Р[х] на Р[a]. Следовательно, y является гомоморфизмом кольца P [x] на кольцо P [a]. Утверждение (d) непосредственно следует из определения отображения y.Поскольку y — гомоморфизм кольца P [x] на P [a], то фактор-кольцо P[x]/Кег y изоморфно кольцу P [a].
Следствие 1.2. Пусть a — трансцендентный элемент над полем P. Тогда кольцо полиномов P [x] изоморфно кольцу P [a].
Доказательство. В силу трансцендентности a над P Kery={0}. Поэтому P[x]/{0}– P [a]. Кроме того, фактор-кольцо кольца P [x] по нулевому идеалу изоморфно P [x]. Следовательно, P [x]– P [a].
ТЕОРЕМА(о строении простого расширения с примитивным алгебраическим элементом):
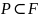 ,
z
– алгебраический над
,
z
– алгебраический над
 ,
p(x)
– min
полином z.
,
p(x)
– min
полином z.
Тогда
 ,
где
,
где

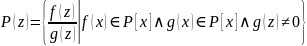
P(z) P(z),
f(x)=f(z)/1
P(z).
Тогда
P(z),
f(x)=f(z)/1
P(z).
Тогда
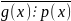 ,
но НОД(g(x),p(x))=1
,
но НОД(g(x),p(x))=1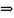 существуют
u(x),v(x)
существуют
u(x),v(x) ,g(x)u(x)+p(x)v(x)=1
,g(x)u(x)+p(x)v(x)=1
g(z)u(z)+p(z)v(z)=1, но p(z)=0 g(z)u(z)=1
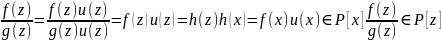
4. Конечное расширение поля.
Пусть
P
— подполе поля F.
Тогда мы можем рассматривать F
как векторное пространство над P,
т. е. рассматривать векторное пространство
F
+ { 0P},где
0P},где
 -
операция умножения элементов из F
на скаляр
-
операция умножения элементов из F
на скаляр
 0P.
0P.
Определение. Расширение F поля P называется конечным, если F, как векторное пространство над P, имеет конечную размерность. Эта размерность обозначается через [F : P].
Cв-во 2.1. Если a — алгебраический элемент степени n над P, то [P (a):P]=n.Это свойство непосредственно следует из теоремы (Пусть a — алгебраический над полем P элемент положительной степени n. Тогда любой элемент поля P(a) однозначно представим в виде линейной комбинации n элементов 1, a, ..., an-1 с коэффициентами из Р.).
Определение. Расширение F поля P называется алгебраическим, если каждый элемент из F является алгебраическим над P.
Теорема 2.2. Любое конечное расширение F поля P является алгебраическим над P.
Доказательство. Пусть n-размерность F над P. Теорема, очевидно, верна, если n = 0. Предположим, что n>0. Любые n+1 элементов из F линейно зависимы над P. В частности, линейно зависима система элементов 1, a, ..., an, т. е. существуют в P такие элементы с0, с1,…,cn не все равные нулю, что с01+ с1a+…+cn an = 0.
Следовательно, элемент a является алгебраическим над P.
Отметим, что существуют алгебраические расширения поля, не являющиеся конечными расширениями.
Теор.2.7 Конечное расширение конечного расширения явл конечным
Пусть F — конечное расширение поля L и L — конечное расширение поля P. Тогда F является конечным расширением поля P и [F : P] = [F : L][ L : P].
Доказательство.
Пусть(1) a1,…,am
— базис поля L
над P
(как векторного пространства) и (2)
 1,…,
n—
базис поля F
над L
. Любой элемент d
из F
можно линейно выразить через базис:(3)
d
= l1
1+...+ln
n
(lk
1,…,
n—
базис поля F
над L
. Любой элемент d
из F
можно линейно выразить через базис:(3)
d
= l1
1+...+ln
n
(lk
 L).
L).
Коэффициенты
1k
можно линейно выразить через базис
(1):(4) lk
= p1k
a
+…+ pmk
am
(pik
P).Подставляя
выражения для коэффициентов lk
в (3), получаем d
=
 pik
ai
k.
i
{1,…,m}k
{1,…,n}.Таким
образом, каждый элемент поля F
представим в виде линейной комбинации
элементов множества B,
где B
= { a
i
k
/{1,...,
m},
k
0 {l,...,
n}}.Отметим,
что множество B
состоит из nm
элементов.Покажем, что B
есть базис F
над полем P.
Нам надо показать, что система элементов
множества B
линейно независима. Пусть (5)
cikai
k
= 0, I,k
pik
ai
k.
i
{1,…,m}k
{1,…,n}.Таким
образом, каждый элемент поля F
представим в виде линейной комбинации
элементов множества B,
где B
= { a
i
k
/{1,...,
m},
k
0 {l,...,
n}}.Отметим,
что множество B
состоит из nm
элементов.Покажем, что B
есть базис F
над полем P.
Нам надо показать, что система элементов
множества B
линейно независима. Пусть (5)
cikai
k
= 0, I,k
где cik 0 P. Так как система (2) линейно независима над L , то из (5) следуют равенства (6) с1ka 1+...+сmka m = 0 (k = 1,..., n).
Поскольку элементы a1, ..., am линейно независимы над P, то из (6) следуют равенства c1k = 0,…,cmk = 0 (k = 1, ..., n),показывающие, что все коэффициенты в (5) равны нулю. Таким образом, система элементов B линейно независима и является базисом F над P.Итак установлено, что [F , P] = nm = [F: L][L: P]. Следовательно, F является конечным расширением поля P
