
- •Примерные вопросы к экзамену по дисциплине «Методы прикладной статистики» для студентов направления «Социология»
- •Понятие о статистических рядах динамики
- •10.Уравнение линейной множественной регрессии. Мнк - оценки параметров уравнения регрессии. Простая линейная регрессия.
- •Постулаты регрессионного анализа.
- •Мнк оценки параметров уравнения регрессии.
- •Свойства мнк оценки вектора
- •Уравнение регрессии со свободным членом.
- •Перспективы развития [править]
10.Уравнение линейной множественной регрессии. Мнк - оценки параметров уравнения регрессии. Простая линейная регрессия.
Уравнение линейной множественной регрессии
y=1x1+2x2+...+mxm+
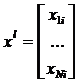 -
вектор независимых переменных,
-
вектор независимых переменных,
i =1,..., m, m p-1
- вектор неизвестных параметров.
- вектор, играющий роль случайной помехи.
(*)- векторное равенство.
yk=1xk1+2xk2+...+mxkm+k, k =1,..., n
 -
случайная компонента, комплексно
характеризующая наличие случайных
ошибок, неучтенных признаков и т.д.
-
случайная компонента, комплексно
характеризующая наличие случайных
ошибок, неучтенных признаков и т.д.Введем в рассмотрение матрицу X:
Тогда уравнение линейной множественной регрессии можно записать в матричном виде:
y=X+
Постулаты регрессионного анализа.
В уравнении регрессии фигурирует матрица X, вектор неизвестных параметров и вектор случайной помехи Поэтому предположения регрессионного анализа касаются этих трех элементов.
1. На нет ограничений, Rm.
2. Вектор - случайный, отсюда y- случайный.
3. Математическое ожидание всех компонент вектора равно 0, M(k)=0, k=1,...,N.
4. Ковариация cov(k,j)=
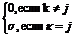 ,
k=1,...,N,
j=1,...,N,
,
k=1,...,N,
j=1,...,N,Замечание:
У различных объектов для различных наблюдений случайные помехи некоррелируемы, а дисперсия конечна и одинакова для всех наблюдений, т.е. условия проведения наблюдений одинаковы для всех объектов.
5. Матрица X - не случайна, т.е. значения независимых признаков известны точно.
6. Ранг матрицы X равен m, т.е. матрица Х имеет m линейных зависимых признаков матрицы X.
Мнк оценки параметров уравнения регрессии.
Суть МНК состоит в следующем: неизвестные параметры выбираются из условия минимума суммы квадратов отклонений фактических значений от расчетных. Сумму квадратов отклонений фактических значений обозначают Q().



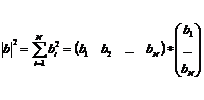
Свойства мнк оценки вектора
1. Оценка МНК линейная по y.
2. Оценка МНК несмещенная.
Определение: Оценка b параметра называется несмещенной, если М(b)=
Доказательство:
Надо доказать, что
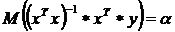 ,
где y=x
,
где y=xМ(у)=М(х+)=М(х)+МхТак как хконстанта
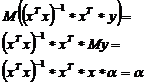
3. МНК-оценка единственная, если справедлив постулат № 6 (доказать самостоятельно)
4. В классе линейных по у несмещенных оценок МНК-оценка обладает минимальной дисперсией, т.е. оценка эффективная.
Уравнение регрессии со свободным членом.
В силу 3-го постулата регрессионного анализа, считается, что эффект неучтенных признаков в среднем равен 0. Это предположение на практике мало правдоподобно. Чаще эффект неучтенных факторов не 0 и вместо постулата 3 вводят постулат 3: M()=m+1=const, где m+1 R.
Тогда уравнение регрессии будет иметь вид:
y=1xk1+...+mxkm+m+1+
 , где
, где 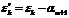 , k=1,...,N
, k=1,...,NТогда
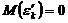
Мы оказались в условиях предыдущей системы постулатов, поэтому далее будем считать, что уравнение регрессии имеет вид:
y=1xk1+...+mxkm+m+1xk,m+1 +
 ,
где
,
где 
т.е. мы ввели фиктивный признак-вектор из единиц. Расширяем матрицу, чтобы остаться в системе постулатов, тогда
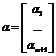 ,
а X(N
,
а X(N (m+1))
(m+1))
Перспективы развития методов прикладной статистики
