2.1. Понятие переходных и установившихся процессов системы, устойчивость и ос
После структуризации системы и установления структур целей и функций элементов системы можно обратиться к процессу функционирования каждого элемента системы.
Выше было определено понятие «состояние» объекта управления как некоторый «срез» поведения его во времени, это внутренние перемены ОУ, некоторый вектор Х, который и будем рассматривать как вектор переменных состояния. Выходной вектор переменных Y в общем случае является функцией вектора Х: G(X, t); t означает, что на объект действуют внешние или внутренние возмущения или параметры функции G(X, t) зависят от времени. На вход объекта поступают управляющие воздействия – вектор U(t) и возмущения (t). В результате структура ОУ примет вид:
Управление – это процесс воздействия на ОУ для выполнения поставленной цели.
Error: Reference source not found
Рис. 2.1
Рассмотрим
i-й
элемент вектора состояния xi(t).
Пусть он находился в некотором начальном
состоянии
(рис. 2.2).
Рис. 2.2
В
момент времени t0
на систему подействовало управляющее
или возмущающее воздействие. В результате
ОУ перешел из состояния
в состояние
.
Этот переход объекта из одного состояния
в другое и называется переходным
процессом, это динамика ОУ. После
завершения в ОУ переходного процесса
в нем устанавливается новое состояние
равновесия
.
Это состояние называется установившимся
процессом или статикой объекта.
Переходный процесс, показанный на рис. 2.2, является устойчивым. Под устойчивостью будем понимать способность ОУ возвращаться в состояние равновесия (может быть, не первоначальное) после действия на него управляющего или возмущающего воздействия. Обычно в результате действия на систему управления U(t) состояние равновесия будет новым, как показано на рис. 2.2. Если же на объект действует возмущение (вредное воздействие (t)), то требуется с помощью правильных управленческих решений вернуть объект в исходное состояние равновесия (рис. 2.3).
Основополагающим принципом управления является принцип обратной связи (ОС), который показан на рис. 2.4.
Желаемое поведение ОУ Y* формируется вышестоящей системой управления (СУ). Задачей управляющей системы данного уровня иерархии является определение Y*(t) и соответствующего ему U*(t).
Рис. 2.3
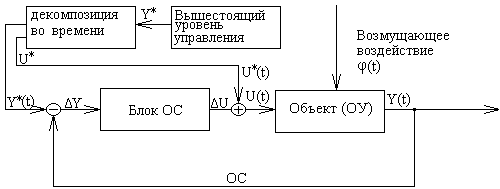
Y*(t) – задающее воздействие, желаемое поведение Y(t)
Рис. 2.4
в блоке ОС определяется ΔY(t) = Y*(t) – Y(t), и на основе этого рассогласования вырабатываются меры воздействия на процесс функционирования ОУ такие, чтобы ΔY(t) = 0. Для этого и служат ОС.
2.2. Управляемость, наблюдаемость, достижимость
Под управляемостью системы нижележащего уровня понимается ее способность выполнять цели и функции, устанавливаемые системой вышестоящего уровня, в противном случае система нижележащего уровня является неуправляемой по всем переменным состояниям или их части. Это требует пересмотра ее структуры или полагаемых целей и функций.
Если систему нижележащего уровня (объект управления) удается формализовать в виде системы линейных ОДУ, то факт управляемости (или неуправляемости) ОУ можно установить аналитически. Пусть имеем систему ОДУ вида
, (2.1)
где Х – вектор переменных состояний, dim X = n; U – вектор управляющих переменных, dim U = m; А и В – постоянные матрицы, dim А = n*n, dim B = n*m.
Критерии управляемости. Линейная стационарная система (2.1) управляема тогда и только тогда, когда
Rank U = rank [B, AB, …, An–1B] = n, (2.2)
где U – матрица управляемости.
Если условие (2.2) не выполняется, то управление U может влиять не на все переменные состояния ОУ. В этом случае возникает необходимость выделять управляемые и неуправляемые переменные. Приведем алгоритм решения задачи. Пусть rank U = r. Это означает, что матрица управляемости имеет только r линейно независимых столбцов e1, e2, …, er. Сформируем матрицу Т по правилу:
T = (T1, T2), dim T = n*n,
где T1 = (e1, …, er); T2 = (er+1, …, en).
Здесь er+1, …, en – любые (n – r) независимых столбцов. Их можно выбрать, например, в виде
.
Все
векторы ei,
i
= 1, n
должны составлять систему из n
линейно независимых векторов, т. е.
.
Сформулируем матрицу:
,
где
матрица Q1
имеет r
строк, а матрица Q2
имеет (n
– r)
строк. Вводя преобразование координат
,
из системы (2.1) получим
,
где
,
,
,
.
В развернутой форме:
(2.3а)
(2.3б)
(2.3а)
(2.3б)
где
;
.
Из
системы (2.3) видно, что подсистема (2.3б)
изменяется во времени в силу собственных
свойств матрицы
и не зависит от управления U.
Обсудим понятие наблюдаемости. Если система нижележащего уровня является «прозрачной» для системы вышестоящего уровня, т.е. эта система может «видеть» значения переменных состояния Х, то нижележащая система является наблюдаемой.
Аналитически наблюдаемость можно установить, если известна модель объекта управления (ОУ) в виде
(2.4)
где
;
.
Критерий наблюдаемости. Объект управления (2.4) является наблюдаемым тогда и только тогда, когда
.
Если rank S < n, то часть переменных Х является ненаблюдаемой. Имеется процедура, позволяющая выявить наблюдаемые и ненаблюдаемые переменные Х.
Достижимость. Состояние системы Х1 называется достижимым из состояния Х0, если существует такое состояние U(t), которое способно перевести систему из состояния Х0 в состояние Х1.
Критерий достижимости тот же, что и критерий управляемости. Эти понятия эквивалентны.