9.4 Ваговий стабілізуючий момент

9.4.1 Ваговий стабілізуючий момент при поперечному нахилі шворня.

Поворот керованих коліс автомобілів здійснюється навколо вісей, які називають осями шворнів. У загальному випадку ці вісі мають нахил у двох взаємно перпендикулярних площинах – поперечній (бічний нахил) і поздовжній. Такий нахил називають комбінованим нахилом шворня. Через нахили шворнів, конструктивні параметри керованого моста і коліс виникає момент, викликаний вагою, що припадає на кероване колесо. Оскільки він залежить від ваги, то його називають ваговим. Величину і напрямок цього моменту необхідно знати під час проектування механізмів кермових керувань автомобілів, оскільки він є складовою частиною моменту опору повороту коліс як на місці, так і під час руху, а також при дослідженні коливань керованих коліс, оскільки під час коливання колеса повертаються навколо вісей шворнів.

Для визначення вагового стабілізуючого моменту були прийняті наступні допущення:

- змінами кутів нахилів шворня і навантаження на кероване колесо, зумовленими перекосом керованого моста під час повороту коліс нехтуємо і вважаємо їх сталими;

- рівнодіюча нормальних реакцій опорної поверхні R_z прикладена в точці перетину площини симетрії ободу з малою віссю контактного відбитка і не залежить від поточного кута розвалу;

- ваговий стабілізуючий момент вважаємо додатним, якщо при фіксованому положенні керованого колеса він напрямлений так, що повертає його в положення прямолінійного руху. Інакше вважаємо момент від'ємним. Прийняте допущення у формулах дозволяє в подальшому врахувати напрямок дії вагового стабілізуючого моменту.

Спочатку розглянемо визначення вагового стабілізуючого моменту тільки від поперечного нахилу шворня. У загальному випадку для отримання аналітичних залежностей для його визначення існують три способи: класичної механіки (добуток сили на плече), аналітичної геометрії (векторний добуток двох векторів) і закон збереження енергії. Як приклад, розглянемо визначення вагового моменту відповідно до способу класичної механіки.

Згідно класичної механіки ваговий стабілізуючий момент М_ст запишемо як добуток сили на плече її дії відносно осі шворня:

М_ст = F  l , (9.9)

де F – сила, перпендикулярна до вісі шворня;

l – плече дії сили F.

Схема для визначення вагового стабілізуючого моменту способом класичної механіки наведена на рис.9.6. Згідно із рис.9.6 прийняті наступні позначення: r_к – радіус колеса; l_ц – довжина цапфи; _ш – кут поперечного нахилу шворня; _ш0 – кут розвалу колеса в положенні прямолінійного руху; R_z – рівнодіюча нормальних реакцій опорної поверхні, викликана вагою, що припадає на колесо.

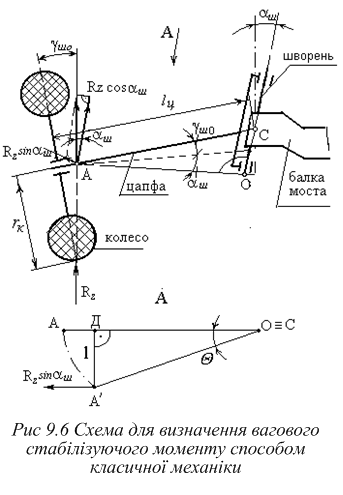Аналіз конструкцій керованих мостів автомобілів засвідчив, що між керованим колесом і віссю шворня існує проміжна ланка – цапфа (див. рис.9.6). Цапфа є важелем відносно осі шворня, і на цьому важелі рівнодіюча нормальних реакцій опорної поверхні створює ваговий стабілізуючий момент. Тому рівнодіючу перенесемо по лінії її дії до перетину з віссю цапфи в точку А.

Оскільки момент створюється складовою, перпендикулярною до вісі шкворня, то розкладемо рівнодіючу на дві складові: R_zsin_ш – перпендикулярну до вісі шворня і R_zcos_ш – паралельну вісі шворня. Отже, силою F у рівнянні (9.9) буде складова R_zsin_ш, прикладена в точці А, оскільки вона перпендикулярна вісі шворня.

Задача зводиться до знаходження плеча l дії сили R_zsin_ш відносно осі шворня.

З аналізу рис. 9.6 випливає, що під час повороту керованого колеса навколо вісі шворня точка А рухатиметься по дузі кола з центром у точці О і радіусом ОА.

Під час повороту цапфи колеса на кут  точка А займе положення А', а плече l у цьому випадку визначиться відстанню l=А'Д.

З аналізу ОА^/Д маємо: А'Д = l = А'Оsin=АОsin ,

де – кут повороту цапфи.

З ОАС запишемо: ОА=АС cos САО==АСсоs .

З аналізу рис.9.6 випливає, що AC = ,

де – поточний кут розвалу, тобто кут розвалу колеса при куті повороту цапфи .

Тоді: l = (l_ц - r_кtg_ш) cos (_ш+_ш0) sin . (9.10)

Після підставлення (9.10) до виразу (9.9), а замість сили F її значення R_zsin_ш отримаємо остаточно значення вагового стабілізуючого моменту від поперечного нахилу шворня при куті поворота цапфи:

Мст( ) = R_zsin _ш(l_ц – r_кtg _ш) cos (_ш+_ш0) sin . (9.11)

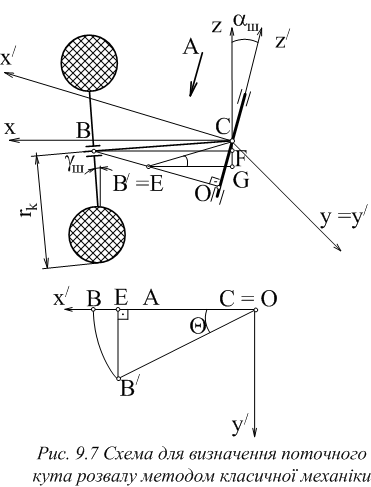
Невідомою величиною у формулі (9.11) є поточний кут розвалу . Розрахункова схема для визначення поточного кута розвалу лівого керованого колеса наведена на рис.9.7. З аналізу рис.9.7 випливає, що під час повороту колеса навколо вісі шворня його центр (точка В) буде переміщатися по дузі кола з центром у точці О і радіусом ОВ. Якщо цапфа обернеться на кут , тоді точка В опуститься на величину FG і займе положення В^'=Е. При такому куті повороту поточний кут розвалу _ш = CВ^'G.

З аналізу СВ^/G маємо:

sin _ш = CG/CB^' = CG/lц.

З аналізу рис.9.7 запишемо:

CG = CF + FG,

де CF = lц • sin _ш0 ; FG = ВЕ • sin _ш.

З рис.9.7 випликає, що:

BE = BO-EO = lц •cos (_ш+_ш0)•(1-cos ).

Підставивши отримані значення до рівняння синуса поточного кута розвалу, після елементарних перетворень отримаємо:

sin _ш = sin _ш0 + cos (_ш+_ш0)•(1-cos ) •sin _ш . (9.12)

Таким чином, використовуючи залежності класичної механіки, отримано залежності (9.11) і (9.12) для визначення вагового стабілізуючого моменту і поточного кута розвалу.

Якщо врахувати, що при малих кутах , , , , тоді вираз (9.12) набуде вигляду:

_ш( )=_ш0+_ш (1-cos ) . (9.13)

Таким чином, ваговий стабілізуючий момент від поперечного нахилу шворня направлений у сторону, що повертає кероване колесо до положення прямолінійного руху автомобіля, а тому буде додатним і його величину будемо визначати за формулами (9.11). (9.13).