Метод Лагранжа (метод виділення повних квадратів)

Метод Лагранжа є методом зведення квадратичної функції до канонічного вигляду. Він полягає в послідовних виділеннях повних квадратів та замінах змінних. Кожна заміна змінних означає перехід до нового базису.

Нехай квадратична функція на скінченновимірному просторі у базисі задається квадратичною формою:

,

і припустимо, що . В дужках збираємо всі доданки, що містять змінну

,

де - деяка квадратична форма від змінних . У дужках виділяємо повний квадрат:

,

де - сума всіх доданків, які не містять змінну . Тоді

,

де - квадратична форма від змінних . Зробимо заміну змінних:

.

Або, в матричному вигляді,

Позначимо

Матриця невироджена, оскільки .

З’ясуємо зміст цієї заміни. Заміна змінних означає перехід до нового базису , причому, якщо вектор у базисі задається координатами , а в базисі - координатами , то

,

або

.

Таким чином, - матриця переходу від базису до базису .

У новому базисі квадратична функція задається квадратичною формою:

.

Далі застосовуємо аналогічні міркування для квадратичної форми .

Припустимо, що в початковій квадратичній формі , але для деякого .Тоді використовуємо аналогічні міркування для змінної .

Окремо розглянемо випадок, коли в початковій квадратичній формі немає квадратів змінних, тобто,

.

Тоді форма складається лише з мішаних добутків змінних і для деякої пари індексів . Припустимо для визначеності, що , і зробимо заміну змінних:

.

У матричному вигляді:

.

Позначимо

Заміна змінних означає перехід від початкового базису до нового базису , причому, якщо вектор у базисі задається координатами: , а в базисі координатами: , то

Тобто, - матриця переходу від базису до базису .

У новому базисі квадратична функція задається квадратичною формою:

,

де квадратична форма складається лише з мішаних добутків змінних.

Продовжуючи цей процес далі, через кроків приходимо до базису простору , у якому квадратична функція задається канонічною квадратичною формою:

Кожний крок алгоритму означає перехід до нового базису. Нехай

- відповідні матриці переходу. Тоді для початкових та заключних змінних виконується рівність:

Це означає, що матриця є матрицею переходу від початкового базису

до заключного базису .

Метод Якобі

Нехай - квадратна матриця порядку . Кутовим мінором порядку матриці називається мінор , побудований на перших рядках та стовпчиках матриці .

Наприклад,

,

тоді

, , .

Будемо казати, що матриця задовольняє умову Якобі, якщо всі її кутові мінори не дорівнюють нулю.

Теорема Якобі (критерій Якобі). Нехай квадратична функція на скінченновимірному векторному просторі у деякому базисі задається матрицею , яка задовольняє умову Якобі. Тоді в просторі існує базис, у якому функції відповідає квадратична форма:

,

де - всі кутові мінори матриці .

Доведення. Припустимо, що в базисі простору квадратичній

функції відповідає матриця

,

яка задовольняє умову Якобі . Через позначимо полярну симетричну білінійну функцію, яка породжує квадратичну функцію . Новий базис простору будемо шукати у вигляді

.

Для знаходження коефіцієнтів припустимо, що вектори задовольняють умови

Знайдемо спочатку вектор

Оскільки , то а тому

.

Припустимо тепер, що вже знайдено вектори , і знайдемо вектор скориставшись умовами

.

Це означає, що

Оскільки то ці рівності можна переписати так:

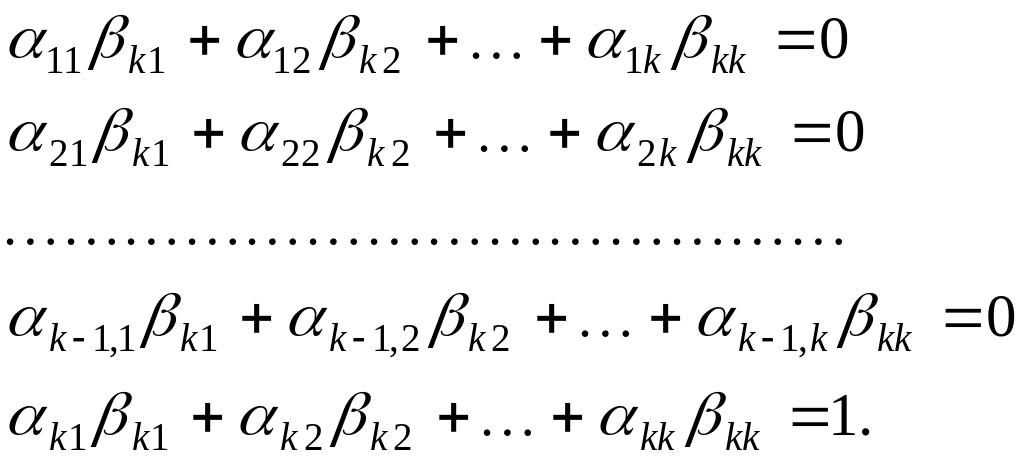
Ми одержали систему лінійних рівнянь відносно невідомих . Система квадратна, її головний визначник співпадає з кутовим мінором матриці . Тобто, , за умовою теореми. Система має єдиний розв’язок, за теоремою Крамера, - , ці значення визначають вектор . Знайдемо за формулою Крамера:

,

де - визначник, який одержується з визначника заміною -го стовпчика на

стовпчик вільних членів. Але

,

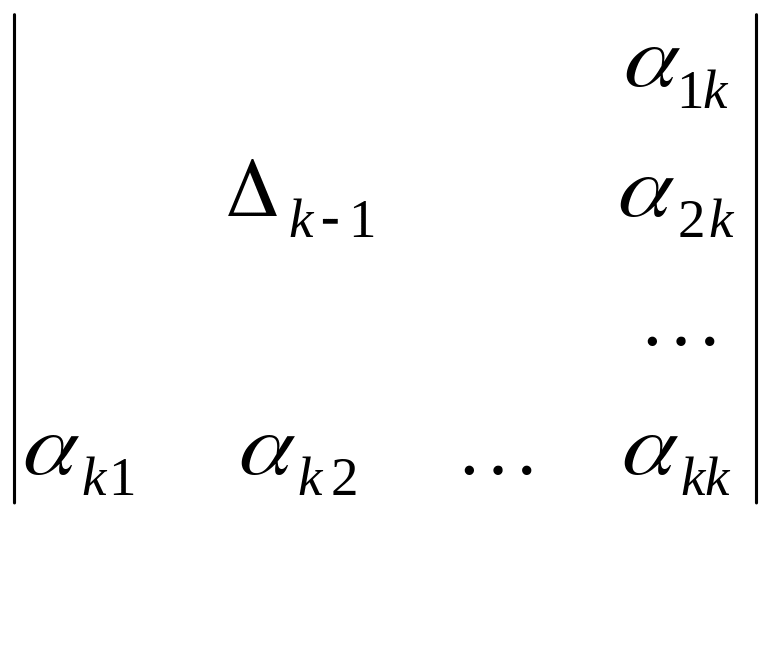тоді

Тому

.

Доведемо тепер, що вектори утворюють базис простору. Оскільки кількість векторів у цій системі співпадає з розмірністю простору, то достатньо довести лінійну незалежність цієї системи. Припустимо супротивне. Тобто, нехай ці вектори лінійно залежні. Оскільки

,

це означає, що деякий вектор лінійно виражається через попередні вектори системи , тобто,

.

Але для кожного індексу вектор лінійно виражається лише через вектори , тоді вектор можна лінійно виразити через вектори :

для деяких . Отже,

Тоді

Оскільки

,

то з останньої рівності вектор можна лінійно виразити через вектори . Цього бути не може, оскільки вектори утворюють базис простору. Таким чином, припущення було не вірним, а тому вектори лінійно незалежні і також утворюють базис простору.

Знайдемо матрицю квадратичної функції у базисі . Припустимо спочатку, що , і, враховуючи принцип побудови векторів , одержуємо:

.

Оскільки матриця симетрична, звідси випливає, що всі її елементи, що стоять поза головною діагоналлю, дорівнюють нулю. Тобто, матриця діагональна.

Знайдемо тепер діагональні елементи:

Таким чином,

.

Тобто, матриця має такий вигляд:

.

Якщо довільний вектор у базисі задається такими координатами: , то

.

Тобто, в базисі квадратична функція задається такою канонічною квадратичною формою: