1.2. Экспериментальная установка и методика исследования, применяемые в нии пмм в рамках изучения этой проблемы.

Исследование проводилось на установке, состоящей из прозрачной кюветы с плоскопараллельными стенками, наполненной рабочей жидкостью, устройства для генерации пузырьков и системы визуализации процесса всплытия одиночного пузырька. Блок-схема экспериментальной установки представлена на рисунке 1. Кювета призматической формы размером 150 150 600 мм изготовлена из оптического стекла толщиной 5 мм. В кювету, установленную строго вертикально, заливался раствор из касторового масла и спирта (в различных процентных соотношениях) объемом 13.5 л. Пузырьки воздуха получали с помощью механизма, позволяющего дозировать объем воздуха (и, следовательно, исходный диаметр пузырька), впрыскиваемого в кювету с жидкостью. Для получения пузырьков фиксированного объема электромотор постоянного тока монтируется с поршнем шприца объемом 100 мл, соединенным посредством полой алюминиевой трубки диаметром 3 мм с выходным отверстием, расположенным в основании кюветы. Питание электромотора осуществляется от источника постоянного тока GPS-4303. Регулируя величину напряжения (в диапазоне 10÷30 В), подаваемого от источника постоянного тока, электромотор приводил в движение поршень. При этом образовывались практически одинакового диаметра пузырьки с начальной скоростью, близкой к нулевой. Отрыв пузырька от поверхности происходил не за счет большого давления (большой скорости потока воздуха), а «естественным» образом, когда равнодействующая всех сил превышала нуль. Также для варьирования размера пузырька использовались сменные иглы диаметром (0.63) мм, расположенные в нижней части кюветы. Система визуализации включала источники света (люминесцентные лампы мощностью 18Вт), установленные на задней панели по всей высоте кюветы, цифровую видеокамеру типа «Panasonic HDC-SD60» и две высокоскоростные видеокамеры Citius C100. Многоракурсная видеосъемка исследуемого процесса позволила повысить точность и обеспечить контроль за изменением параметров всплытия пузырька на различных стадиях его движения. Первая камера фиксировала динамику пузырька на начальном нестационарном этапе движения, вторая – на всей траектории пузырька. Видеосъемка проводилась с разрешением 1280 670 со скоростью свыше 700 кадр/сек и временем экспозиции 1/500÷1/2000 с. Третья камера использовалась для определения размера пузырька; область съемки составляла 5 5 см с увеличением в 2 раза.

Для измерения расстояния, пройденного пузырьком, использовалась масштабная линейка с ценой деления 1мм, изначально отградуированная с учетом оптического искажения регистрационной видеоаппаратуры.

Рисунок 1 – Схема экспериментальной установки по исследованию скорости всплытия одиночного сферического пузырька: 1 – кювета; 2 – жидкость;

3 – пузырек; 4 – генератор пузырьков; 5 – видеокамеры; 6 – компьютер;

7 – оптическая скамья

В большинстве работ, посвященных исследованию динамики движения частицы дисперсной фазы (капли, пузырька или твердой частицы), в качестве рабочей жидкости используется водно-глицериновый раствор []. Однако физико-химические свойства (вязкость, плотность) данного раствора в сильной степени зависят от внешних условий (температуры, влажности) и существенно изменяются при изменении температуры даже на 1 []. Поэтому для обеспечения прецизионных измерений необходимо использовать жидкость со стабильными во все время эксперимента к изменениям условий окружающей среды свойствами. В данной работе использовалось касторовое масло и его растворы со спиртом. В диапазоне рабочих температур (17÷22 ) выбранный раствор сохраняет значения физико-химических свойств неизменными.

Определение параметров экспериментов. Перед началом и в конце каждого эксперимента проводились измерения вязкости и плотности раствора касторовое масло – спирт.

Вязкость раствора измерялась путем решения обратной задачи о гравитационном осаждении твердой сферической частицы в Стоксовском режиме. В качестве частиц использовались стальные шарики диаметром 2.005 мм. Диаметр частиц измерялся микрометром с погрешностью ±0.001 мм. Плотность стальных частиц измерялась следующим образом. На аналитических весах определялся вес N=100 частиц с погрешностью ±0.01 г. Плотность частиц рассчитывалась по формуле

,

где – вес 100 частиц, в граммах. Плотность стальных шариков составляла ±0.001 кг/м³. Экспериментальная плотность близко совпадает с табличным значением плотности материала выбранных частиц [].

Суть измерения вязкости данным способом состоит в следующем. Времяпролетным методом определялась скорость осаждения шарика на стационарном участке движения. Время осаждения шарика определялось секундомером с погрешностью ±0.1 с. В проведенных экспериментах значение варьировалось в диапазоне (0.013÷0.065)±0.001 м/с. Используя формулу для скорости гравитационного осаждения частиц в Стоксовском режиме, находим вязкость раствора

где – плотность частицы; – плотность раствора; – диаметр частицы; g=9.80665м/с² – ускорение свободного падения; – скорость стационарного осаждения частицы.

Плотность раствора определялась ареометром с погрешностью ±1 кг/м³ и варьировалась в диапазоне (935÷960) кг/м³.

Абсолютная погрешность определения вязкости раствора (границы доверительного интервала) оценивалась по формуле

и составляла ±0.1 Па·с. В проведенных экспериментах величина изменялась в пределах 0.2÷1.1 Па·с.

Время и длина участка установления стационарной скорости шарика оценивались формулами

(9)

Согласно данным формулам отклонение скорости от стационарной не превышает 1%.

Зависимости и , рассчитанные для условий проведенных экспериментов, представлены на рисунке 2.

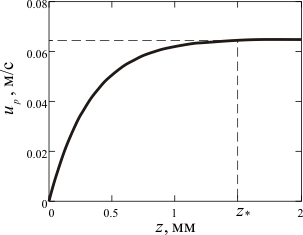
Рисунок 2 – Зависимость скорости гравитационного осаждения стального шарика от времени и пройденного расстояния ( =0.2 Пас)

Время и длина участка стабилизации, рассчитанные по формулам (9), при осаждении шарика в наименее вязкой жидкости ( =0.2 Пас) составляют =31 мс, 1.5 мм. Для более вязкой жидкости значения и будут меньше. Следовательно, квазистационарный режим движения шарика устанавливается практически сразу же после помещения его в раствор.

С целью контроля режима осаждения стальной частицы рассчитывалось число Рейнольдса Re_p= . Во всех экспериментах значение числа Рейнольдса составляло Re_p<1.

С учетом заданной разрешающей способности видеокамеры, геометрические размеры пузырьков определялись с относительной погрешностью менее 3%.

Пройденный пузырьком путь и скорость определялись путем покадровой обработки результатов скоростной видеосъемки. Скорость всплытия пузырька на некоторой высоте (где – номер кадра) вычислялась по формуле

,

где , – пройденное пузырьком расстояние на и кадрах, соответственно; – интервал времени между и кадрами; N – количество кадров.

Пройденное пузырьком расстояние измерялось при помощи компьютерной программы CorelDRAW с погрешностью ±0.5 мм. Погрешность в измерениях возникает из-за искажения изображения и зависит от разрешающей способности видео системы. Измерения скорости всплытия пузырька на начальном (нестационарном) участке проводились для значения 5 мм; погрешность определения не превышала 10%.

Погрешность определения скорости всплытия на стационарном участке, обусловленная разбросом результатов 3 5 дублирующих опытов, не превышала 0.1% при значении доверительной вероятности =0.95.