Паралельність (наслідки з аксіом)

Т₄: Плоскость разбивает пространство на два полупространства.

Если т. Х и У одному полупространству, то отрезок ХУ не пересекает плоскость. Если же т. Х и У  разным полупространствам, то отрезок ХУ пересекает плоскость разбиения.

Аналог разбиения пл-ти на

І две полуплоскости

У ІІ a

У K

Х Х

 Х Z

Вопросы:

1. Какие аксиомы используются при доказательстве этой теоремы?

2. Какие теоремы используются при доказательстве этой теоремы?

Закріплення вивченого матеріалу. Розв'язання задач.

№ 2. Можно ли через точку пересечения двух данных прямых провести третью прямую, не лежащую с ними в одной плоскости? Объясните ответ.

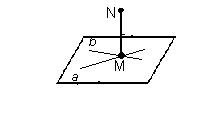
Пусть прямые а и в пересекаются в

точке М. Тогда, согласно аксиомы С_3,

через них можно провести плоскость α.

По аксиоме С₁, всегда существуют точки,

которые не принадлежат плоскости α. Возьмем точку N  плоскости α. Через

две точки можно провести прямую.

Соединим М и N. Прямая МN плоскости α, но проходит через точку пересечения прямых а и в. Следовательно через точку пересечения двух прямых можно провести третью прямую, которая не лежит сними в одной плоскости.

№ 3. Точки А, В, С, лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.

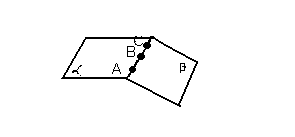
Пусть точки А,В,С  одновременно плоскости α и плоскости β. Тогда по

аксиоме С₂, плоскости β и α пересекаются

по прямой а, которая содержит все три

точки А, В и С. Следовательно, точки

А, В, С лежат на одной прямой а, которая

Является линией пересечения плоскостей α и β.

№ 4. Даны три различные попарно пересекающиеся плоскости. Докажите, что если две из прямых пересечения этих плоскостей пересекаются, то третья прямая проходит через точку их пересечения.

Плоскость γ пересекается с плоскостью α с

по прямой в. Плоскость α пересекается с

плоскостью β по прямой с. Плоскость β α β

пересекается с плоскостью γ по прямой а.

Пусть прямые а и в пересекаются в точке О.

Т огда точка О  β (поскольку а β), плоскости γ, О а

(поскольку в γ) и плоскости α (поскольку в α). в γ

Следовательно, плоскости α и β имеют общую

точку О. По аксиоме С₂ точка О лежит на прямой

пересечения плоскостей α и β, то есть на прямой с. Таким образом, прямая с проходит через точку пересечения прямых а и в, что и требовалось доказать.

№ 6. Четыре точки не лежат в одной плоскости. Могут ли какие-нибудь три из них лежать на одной прямой? Объясните ответ.

А

Предположим, что из четырех точек, которые не лежат

в одной плоскости, три точки лежат на одной прямой. С

Тогда через эту прямую и оставшуюся точку можно

п ровести плоскость. Но это противоречит условию В

задачи. Следовательно, наше предположение неверно,

то есть не могут три точки из четырех данных а

лежать на одной прямой. Д

№ 10. Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Пусть даны точка А и прямая а. Через данные в

прямые и точку можно провести плоскость α. Пусть В α

через точку А проходят прямые в, в₁ и в₂, которые в₁ В₁

п ересекают прямую а в точках В, В₁, В₂. Но все

точки прямой а принадлежат плоскости α. А

Получили, что каждая из данных прямых имеет в₂ В₃

С плоскостью α две общие точки. Следовательно а

Прямые в, в₁, в₂ лежат в плоскости α. Очевидно,

Что любая прямая, проходящая через точку А и пересекающая прямую а, лежит в плоскости α.