19.4.2. Цилиндрический конденсатор

Цилиндрический конденсатор представляет собой устройство из двух цилиндрических обкладок, имеющих общую ось ( коаксиальных ), разделенных слоем диэлектрика цилиндрической формы.

Электрическое поле такого конденсатора представляет собой суперпозицию двух полей цилиндрических поверхностей, имеющих равные по величине, но противоположные по знаку заряды.

Напряженность такого электрического поля

Разность потенциалов между обкладкам

где R₁ и R₂ - соответственно радиусы внутренней и внешней обкладок.

Таким образом

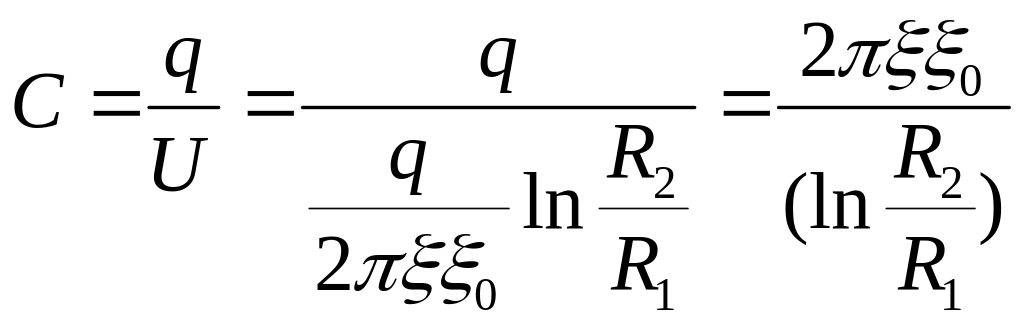
При d = R₂ - R₁ << R₁

, 2.29

где d = R₂ - R₁ - расстояние между обкладками.

Тогда

2.30

Следовательно, при указанных условиях, емкость цилиндрического конденсатора с определенной степенью точности можно рассчитывать по формуле емкости плоского конденсатора.

Сферический конденсатор

Сферический конденсатор представляет собой устройство, состоящее из двух сферических поверхностей, которые имеют общий центр, различных радиусов, разделенных сферическим слоем диэлектрика.

Напряженность электрического поля между обкладками такого конденсатора

Разность потенциалов между обкладками

2

Таким образом

2.33

При R₂ - R₁ = d << R₁ R₂

,

т.е. емкость сферического конденсатора можно с определенной степенью точности рассчитывать по формуле емкости плоского конденсатора.

Соединения конденсаторов

Существует два вида соединения конденсаторов: последовательное и параллельное.

Последовательное соединение конденсаторов

При последовательном соединении каждая из обкладок какого-ли­бо конденсатора соединяется только с одной обкладкой другого кон­денсатора, образуется цепочка конденсаторов. К крайним обкладкам такой цепочки прикладывается соответствующее напряжение, под дейс­твием которого происходит перераспределение электрических зарядов, при этом заряды на всех промежуточных обкладках равны по величине, но чередуются по знаку.

В результате перераспределения зарядов, заряд батареи ( це­почки ) равен заряду одного конденсатора. Напряжение между обкладками отдельно взятого конденсатора обратно пропорционально его емкости, а напряжение батареи равно сумме напряжений каждого из входящих в её конденсаторов.

Следовательно такое соединение конденсаторов применяется в тех случаях, когда необходимо получить емкость, работающую при высоких напряжениях.

Так как в рассматриваемом случае

q₁ = q₂ = … = q = const, a U = U₁ + U₂ + … +U_n=U_i 2.35 2.36

, 2.37

или

2.38

Таким образом, при последовательном соединении, величина об­ратная емкости батареи равна сумме величин обратных емкости от­дельных конденсаторов.

Если емкости отдельных конденсаторов равны

C₁ = C₂ = C₃ = ..... , 2.39

то

, 2.40

а

, 2.41

т.е. при последовательном соединении n одинаковых конденсаторов,

емкость батареи в n раз меньше емкости одного конденсатора.