8.1. Классическая электронная теория электропроводности металлов и ее опытные обоснования

Металлы - проводники электрического тока . Строение металлов - кристаллическая решетка и свободные электроны . Атомы объединяясь в кристаллическую решетку обезличили большое количество электронов , тогда уместно применение ранее разработанной теории идеального газа .

Итак физическая модель электропроводимости — “ идеальный электронный газ “ .

Электрический ток - направленное движение свободных электронов в металле это “электронный идеальный газ “. Для молекулы идеального газа справедливо соотношение :

на электрон находящийся в электрическом поле действует сила :

:

Таким образом применяя для электронного газа в металлах модель идеального газа мы получили сугубо теоретически формулу экспериментального закона Ома, что является убедительным подтверждением правильности выбранной нами модели .

Аналогично

Закон Джоуля-Ленца:

предположим , что в момент удара вся кинетическая энергия электрона переходит в тепло , тогда при ударе n- электронов за время t количество выделившегося тепла определяется :

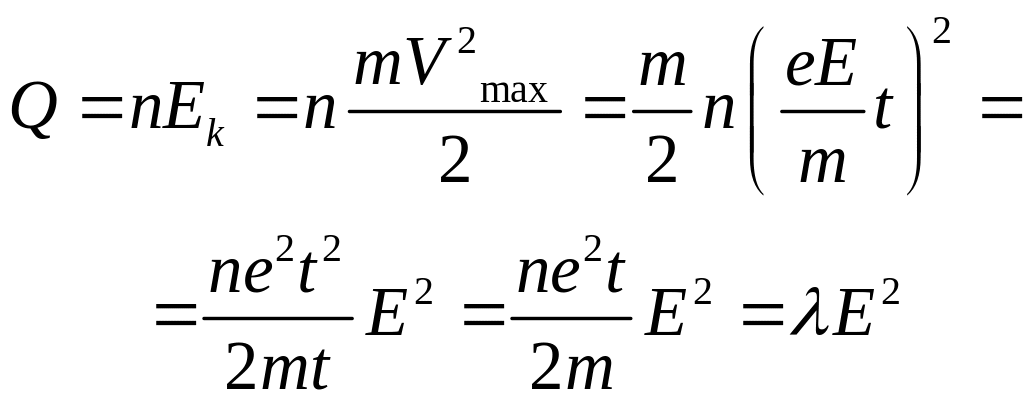
Совершенно просто такое представление об электронах как об “электронном газе” объясняет электросопротивление металлов:

электроны сталкиваясь с узлами электронной кристаллической решетки теряют свою скорость, а значит способность перемещаться и нагревают металл.

Проанализируем формулу:

e - заряд электрона

13. Масса электрона

14. Количество электронов (у всех металлов примерно одинакова)

t - время от столкновения до столкновения (так как размеры кристаллической решетки мало различаются у разных металлов, то t у всех металлов примерно одинаково

8.3. Закон Джоуля-Ленца в дифференциальной и интегральной формах.

Двигаясь под действием силы F = eE, электрон проводимости приобретает некоторую энергию

. (6.53)

Провзаимодействовав с ионом кристаллической решетки, он отдает ему эту энергию, которая выделяется в проводнике в виде тепла.

Если взаимодействие электрона проводимости с ионом кристаллической решетки происходило в течение времени t, то за это время в проводнике выделится в виде тепла энергия

, (6.54)

где – число взаимодействий электрона проводимости с ионом кристаллической решетки.

Так как

то

, (6.55)

где

– время свободного пробега электрона проводимости.

Если в объеме проводника содержится n электронов проводимости, то энергия, переданная единице объема проводника в единицу времени всеми электронами,

. (6.56)

Выражение (6.56) является математической формой записи закона Джоуля-Ленца в дифференциальной форме.

Из формулы (6.56) можно получить формулу закона Джоуля Ленца в интегральной форме. Имеем

,

где  = 1/;

E = U/dl,

dV = S dl.

Следовательно,

или

, (6.57)

где

- сопротивление проводника;

U = IR – напряжение.

Количество тепла, выделившееся в проводнике за время t,

. (6.58)

Выражение (6.58) является математической формой записи закона Джоуля-Ленца в интегральной форме.

В случае постоянного тока

. (6.59)

Классическая электронная теория проводимости металлов смогла объяснить не только электропроводность металлов и сплавов, но и их теплопроводность, некоторые оптические свойства вещества, что является её крупным достижением. Однако с её помощью невозможно объяснить такие экспериментальные факты, как независимость теплоемкости металлов от наличия электронов проводимости и сверхпроводимости. Это связано с тем, что в ней электроны проводимости подчиняются законам идеального газа, законам статистики Максвелла-Больцмана. В действительности же для электронов проводимости справедлива квантовая статистика, и они подчиняются закону статистики Ферми-Дирака.