Билет № 9.

3. Найдите длину окружности, если известно, что площадь круга равна 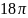см².

Решение. Площадь круга 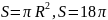см2. Тогда R = см.. Длина окружности вычисляется по формуле: . С = 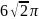см. Ответ. см.

3. Найдите радиус окружности, вписанной в треугольник ВСЕ, если она касается стороны ВС в точке Р и известно, что ВЕ = ВС = 15 см, СР = 12 см.

Решение. Пусть К – точка касания окружности с основанием ЕС . Тогда по теореме об отрезках касательных СК = СР = 12 см, ЕС = 24 см. ВК – медиана, высота (по свойствам равнобедренного треугольника). Из прямоугольного треугольника ВКС по теореме Пифагора: . Площадь треугольника АВС S = 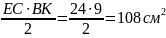. С другой стороны, S= Pr:2. Откуда r =108: (54:2) = 4 см. Ответ. 4см.

Билет № 10.

3. Найдите число сторон выпуклого многоугольника, сумма внутренних углов которого равна 4320⁰.

Решение. Сумма внутренних углов выпуклого многоугольника вычисляется по формуле 1800(n – 2) = 43200. Решив уравнение, получим, n = 26. Ответ. 26.

3. В остроугольном треугольнике АВС угол А равен 60⁰, ВС = 10 см, отрезки ВМ и СК – высоты. Найдите длину отрезка КМ.

Решение. Треугольники АВМ и АКС подобны по 2-м углам (угол А – общий, 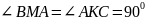) 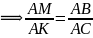(1) Из пропорции (1) получим: 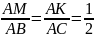, 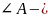общий для треугольников АКМ и АВС.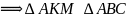 по двум сторонам и углу между ними 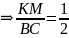, откуда КМ = 5 см. Ответ.5 см .

Билет № 11.

3. Найдите медиану, проведенную к гипотенузе прямоугольного треугольника, если известно, что его катеты равны 8 см и 6 см.

Решение. Пусть a и b – катеты, m – медиана, а c – гипотенуза прямоугольного треугольника. Медиана прямоугольного треугольника равна половине гипотенузы. По теореме Пифагора 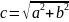, с = 10 см, m = 5 см. Ответ. 5см.

3. Найдите радиус окружности, описанной около трапеции, если известно, что средняя линия трапеции равна 14см, боковая сторона равна 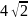см, а одно из оснований трапеции является диаметром описанной окружности.

Решение. Обозначим R = AD:2 – радиус окружности, х = BC – меньшее основание трапеции, СН – высота. Так как средняя линия трапеции равна 14 см, то 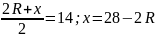. 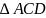– прямоугольный, т.к. угол ACD опирается на диаметр.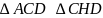 по двум углам ( 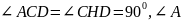– общий) 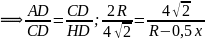. 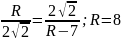см Ответ. 8 см.

Билет № 12.

3. В прямоугольный треугольник вписана окружность радиуса 4 см. Найдите периметр этого треугольника, если известно, что его гипотенуза равна 26 см.

Решение. Рассмотрим прямоугольный треугольник АВС : 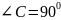, АВ = 26 см, К, Т, М – точки касания окружэности соответственно со сторонами АС, АВ, ВС. КОМС – квадрат, ОК = ОМ = КС = СМ = 4см. По свойству отрезков касательных: АТ = АК = х, ВТ = ВМ = у, х + у = АВ = 26см. Найдем периметр треугольника АВС: Р = АВ+АС+ВС = АВ+АК+КС+СМ+МВ = 26+х+4+4+у = 60 см. Ответ. 60 см.

3. Две стороны параллелограмма равны 13 см и 14 см, а одна из диагоналей равна 15 см. Найдите площадь треугольника, отсекаемого от параллелограмма биссектрисой его угла.

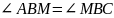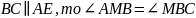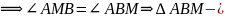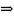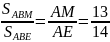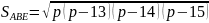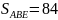Решение. Рассмотрим параллелограмм АВСЕ: АВ = 13см, АЕ = 14см, ВЕ = 15см, ВМ – биссектриса. Т.к. ВМ – биссектриса, то ; т.к. как накрест лежащие. равнобедренный АВ=АМ=13 см По теореме об отношении площадей треугольников, имеющих равные высоты, . По формуле Герона , где p = Р/2=21см см2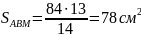 . Ответ. 78 см2.