Билеты по геометрии для 9 класса. Практическая часть. Решения и ответы.

Билет №1.

3. Найдите диагонали равнобедренной трапеции, основания которой равны 4см и 6см, а боковая сторона равна 5см.

   Решение. Рассмотрим равнобедренную трапецию АВСЕ. Проведем высоту АН и диагональ ВЕ. АН = (АЕ – ВС):2 = 1 см Из треугольника АВН по теореме Пифагора: 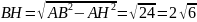см. НЕ = АЕ – АН = 5 см Из треугольника ВЕН по теореме Пифагора: 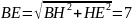см. Ответ. 7см

4. В окружности радиуса 6см проведена хорда АВ. Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е. Известно, что СМ = 9см, угол АСВ = 30⁰. Найдите длину отрезка СЕ.

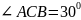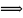
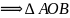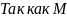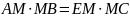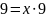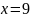
Решение. –вписанный. – центральный. – равносторонний и АВ = АО = ВО = 6 см. − середина отрезка АВ, то АМ = АВ = 3 см. Пусть ЕМ = х. По теореме об отрезках пересекающихся хорд: , , Тогда ЕС = ЕМ + МС = 1 + 9 = 10 см. Ответ. 10 см.

Билет №2.

3. Углы ADC и АВC вписаны в окружность. Какой может быть величина угла ADC, если известно, что 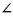АВС = 56⁰?

   Решение. 1 случай: точки В и D лежат по одну сторону от хорды АС. Тогда 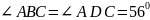как вписанные, опирающиеся на одну дугу. 2 случай: точки В и D лежат по разные стороны от хорды АС. Тогда 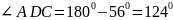. Ответ. 560 или 1240.

4. Дана прямоугольная трапеция ABCD ( AD – большее основание , AB 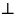AD). Площадь трапеции равна 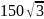см², 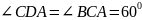. Найдите диагональ АС.

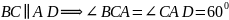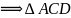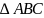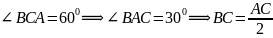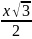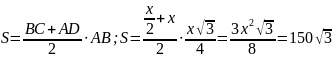
Решение. (как накрест лежащие при секущей АС) – равносторонний. – прямоугольный, . Пусть АС = х. Тогда ВС = х/2, АD = х, АВ = . Площадь трапеции выразим по формуле: Решая уравнение, получим, х = 20. Ответ. 20 см.

Билет №3.

3. Найдите площадь круга, если длина окружности равна 8 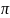см.

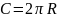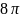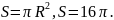
Решение. Длина окружности вычисляется по формуле: . Так как С = см, то R = 4 см. Тогда площадь круга Ответ.

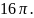
3. Площадь параллелограмма равна 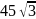см2, 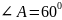, AB : AD = 10 : 3. Биссектриса угла А пересекает сторону параллелограмма в точке М. Найдите длину отрезка АМ.

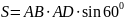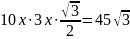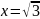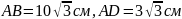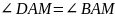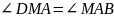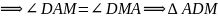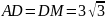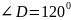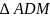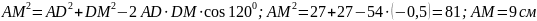
Решение. Пусть АВ = 10х см, AD = 3х см. Так как площадь параллелограмма , то , . Значит, . , так как АМ – биссектриса, как накрест лежащие – равнобедренный , , . Из по теореме косинусов: Ответ. 9 см.

Билет №4.

3. Величины углов АВС и КВС относятся как 7 : 3, а их разность равна 72⁰. Могут ли эти углы быть смежными?

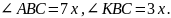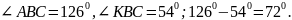
Решение. Пусть Если эти углы смежные, то 7х + 3х = 1800, х = 180 Тогда Ответ. Да, могут.

3. Найдите радиус окружности, вписанной в параллелограмм, если его диагонали равны 12см и 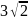см.

Решение. Рассмотрим параллелограмм АВСЕ, АС = 12, ВЕ = . Так как АВСЕ – описанный 4-угольник, то ВС + АЕ = АВ + ЕС. Так как АВСЕ – параллелограмм, то АВ = СЕ, АЕ = ВС. Значит, АВ = ВС = СЕ = АЕ и, следовательно, АВСЕ – ромб и по свойству диагоналей ромба, АС ВЕ. Рассмотрим прямоугольный треугольник АВО: АО = АС:2 = 6 см, ВО = ВЕ:2 = 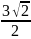см. По теореме Пифагора: 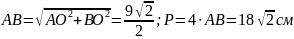. Так как окружность вписана в ромб, то 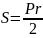. . 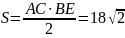Откуда получаем: r = 2 см. Ответ. 2 см.

Билет № 5.

3. В равностороннем треугольнике АВС проведена высота ВР. Найдите углы треугольника АВР.

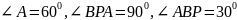
Решение. Высота в равностороннем треугольнике является медианой и биссектрисой, поэтому, Ответ. 300, 600, 900.

3. Найдите диагональ А₁А₃ правильного восьмиугольника А₁А₂ …А₈, если площадь треугольника А₁А₂А₅ равна 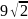м².

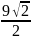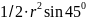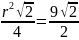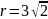Решение. В правильном восьмиугольнике диагональ А1А5 – диаметр описанной окружности, тогда отрезок А2О – медиана прямоугольного треугольника А1А2А5. Значит, площадь треугольника А1А2О S1 = . Центральный угол А1ОА2 = 3600 : 8 = 450. Так как ОА1 = ОА2 = r , то площадь треугольника А1А2О S1 = . Получим уравнение: ; . В А1А3О угол А1ОА3 – прямой. Тогда по теореме Пифагора: А1А32 = ОА12 + ОА32 = 2r2, А1А32 = 36; А1А3 = 6. Ответ. 6 м.