4.7Звено чистого запаздывания

Под звеном чистого запаздывания понимается устройство, в котором выходной сигнал повторяет закон изменения входного после выдержки времени, называемого временем запаздывания.

Примером звена чистого запаздывания может являться тиристорный преобразователь переменного напряжения в постоянное. Силовые вентили преобразователя открываются с помощью импульсов управления, положение которых относительно питающего напряжения зависит от напряжения задания. При этом, так как тиристоры закрываются под действием сетевого напряжения, изменение угла отпирания произойдет только в следующий момент подачи импульса отпирания, то есть с задержкой по времени. Запаздыванием характеризуется также работа импульсных устройств, например аналого-цифрового преобразователя. Механизмы, работающие в транспортных устройствах (транспортеры, конвейеры и т.д.), также представляются звеном чистого запаздывания.

Зависимость выходного сигнала от сигнала на входе звена записывается следующим выражением:

(4.103)

где τ – время запаздывания.

Уравнение в операторной форме записи принимает следующий вид:

. (4.104)

4.7.1 Передаточная функция

. (4.105)

Условно-графическое обозначение звена чистого запаздывания представлено на рисунке 4.13.

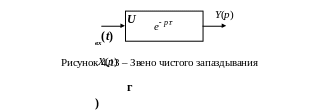
Если время запаздывания значительно меньше постоянных времени заданной САУ, передаточную функцию звена чистового запаздывания посредством разложения в ряд Тейлора заменяют следующим выражением:

. (4.106)

4.7.2 Переходная функция

(4.107)

График переходной функции представлен в таблице 4.11.

4.7.3 Амплитудно-фазочастотная характеристика

4.7.3.1Амплитудно-фазочастотная характеристика

. (4.108)

4.7.3.2Амплитудночастотная характеристика

. (4.109)

4.7.3.3Фазочастотная характеристика

. (4.99)

4.7.3.4Вещественная частотная характеристика

. (4.1100)

4.7.3.5Мнимая частотная характеристика

. (4.111)

Графики амплитудно-фазочастотных характеристик представлены в таблице 4.11.

4.7.4 Логарифмическая амплитудно-фазочастотная характеристика (ЛАФЧХ)

4.7.4.1Логарифмическая амплитудночастотная характеристика (ЛАЧХ)

. (4.112)

4.7.4.2Логарифмическая фазочастотная характеристика (ЛФЧХ)

. (4.113)

Графики логарифмических амплитудно-фазочастотных характеристик представлены в таблице 4.11.

На рисунке 4.14 представлены временные характеристики входного и выходного синусоидальных напряжений при разных частотах. Из графиков видно, что амплитуда выходного сигнала не изменяется при увеличении частоты входного синусоидального сигнала, однако фазовый сдвиг постепенно увеличивается до бесконечности (рисунок 4.14).

Таблица 4.11 – Звено чистого запаздывания

Дифференциальное уравнение	Передаточная функция	Переходная характеристика
		Уравнение	График
АФЧХ		ЛАФЧХ
Уравнение	График	Уравнение	График