12 .Зависимость между непрервностью функции и дифференцир-ю. Правила дифференцирования. Таблица производных.

Если функция дифференцируема в точке x, то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то то ее приращение представимо в виде  y =A x + ( x)  x,, из которого следует, что lim_ x 0 y = 0, что означает непрерывность функции в данной точке.

Правила дифференцирования.

f(x), функция для которой  нужно найти производную	f´(x), преобразованная функция
(u + v)'	u' + v'
(u - v)'	u' - v'
(uv)'	u'v + v'u
(u/v)'	( u'v - v'u ) / v2
(cf)'	c*f '

Пояснения к таблице.  u, v - произвольные функции  c - константа 

1. Дифференциал суммы функций равен сумме дифференциалов каждого из слагаемых

2. Дифференциал разности равен разности дифференциалов

3. Дифференциал произведения функций равен произведению дифференциала первого слагаемого на второе слагаемое плюс дифференциал второго слагаемого умноженный на первое слагаемое

4. Дифференциал частного двух функций равен дроби, числитель которой равен производной делимого, умноженной на делитель, минус производная делителя, умноженная на делимое, а знаменатель - квадрату делителя

5. Дифференциал произведения константы на функцию равен произведению этой константы на дифференциал данной функции

Производные простых функций

1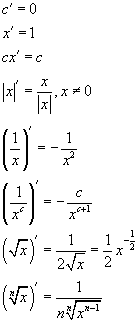 . Производная от числа равна нулю  с´ = 0  Пример:  5´ = 0  2. Производная переменной равна единице  x´ = 1  3. Производная переменной и множителя равна этому множителю  сx´ = с  Пример:  (3x)´ = 3

Откуда следует, что  (cx + b)' = c  то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k). 

4. Производная переменной по модулю равна частному этой переменной к ее модулю  |x|' = x / |x| при условии, что х ≠ 0  5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу  ( x^c )'= cx^c-1, при условии, что x^c и сx^c-1,определены а с ≠ 0  Пример:  (x² )' = 2x  (x³)'  = 3x²  Простыми словами, снесите степень переменной "вниз" как множитель, а потом уменьшите саму степень на единицу. Например, для x²  - двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам х. То же самое произошло для x³ - тройку "спускаем вниз", уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x² . Немного "не научно", но очень просто запомнить.  6. Производная дроби 1/х  (1/х)' = - 1 / x²  Пример:  (1/x)' = (x^-1 )' , тогда можно применить формулу из правила 5  (x^-1 )' = -1x^-2 = - 1 / х²  7. Производная дроби с переменной произвольной степени в знаменателе  ( 1 / x^c )' = - c / x^c+1  Пример:  ( 1 / x² )' = - 2 / x³  8. Производная переменной под квадратным корнем  ( √x )' = 1 / ( 2√x )   или 1/2 х^-1/2  Пример:  ( √x )' = ( х^1/2 )'   значит можно применить формулу из правила 5  ( х^1/2 )' = 1/2 х^-1/2 = 1 / (2√х)  9. Производная переменной под корнем произвольной степени  ( ⁿ√x )' = 1 / ( n ⁿ√x^n-1 )