7. Бесконечно большие функции. Второй замечательный предел. Некоторые замечательные пределы.

Функция   называется бесконечно большой при  , если для любого положительного числа   существует такое число  , что для всех  , удовлетворяющих неравенству  , выполняется неравенство  . Записывается:  .

Данный факт носит название второго замечательного предела.

Справка:   – это иррациональное число.

В качестве параметра   может выступать не только переменная  , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.

Пример

Найти предел 

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение   , по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.

Нетрудно заметить, что при   основание степени  , а показатель –  , то есть имеется, неопределенность вида  :

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр  , значит, в показателе нам тоже нужно организовать   . Для этого возводим основание в степень  , и, чтобы выражение не изменилось – возводим в степень  :

Когда задание оформляется от руки, карандашом помечаем:

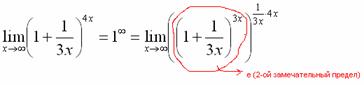Практически всё готово, страшная степень превратилась в симпатичную букву  :

При этом сам значок предела перемещаем в показатель:

Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

8. Непрерывность и точки разрыва функции

Функция f (х) называется непрерывной в точке х₀, если при х—> х₀ предел функции существует и равен ее частному значе­нию в этой точке, т. е. если lim f(х) = f(x₀).

 x->х₀ 

Для непрерывности функции f(х) в точке х₀ необходимо и достаточно выполнение следующих условий:

1)функция должна быть определена в некотором интервале, содержащем точку х_0.(т. е. в самой точке х₀ и вблизи этой точки);

2) функция должна иметь одинаковые односторонние пределы

 lim f (х) = lim f (x);

 x->х₀ -0  x->х₀ +0   

3) эти односторонние пределы должны быть равны f (x₀).

Функция f (x) называется разрывной в точке х₀, если она опре­делена в сколь угодно близких точках, но в самой точке х₀ не удовлетворяет хотя бы одному из условий непрерывности.

Разрыв функции f(х) в точке х₀ называется конечным, или 1-го рода, если существуют конечные односторонние пределы

 lim f(x) и lim f(х).

 x-> х₀ -0 x-> х₀ +0

 Все другие случаи разрыва функции называются разрывами- 2-го-рода; в частности, если хотя бы один из указанных односторонних пределов окажется бесконечным, то и разрыв функции называется бесконечным.

9. Свойства функций, непрерывных на отрезке

Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.

Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.

Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О[a, b] рис2

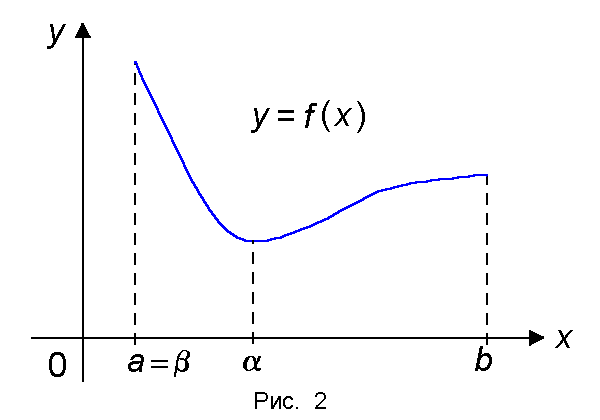
Наибольшее значение M обозначается символом maxx О [a, b] f(x), а наименьшее значение m — символом minx О [a, b] f(x).

Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.

Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).

10. Задачи,приводящие к понятию производной

Задача о скорости движущейся точки.  

Пусть s = s (t) представляет закон  прямолинейного движения материальной точки.  

Это уравнение выражает путь s, пройденный  точкой, как функцию времени t.  

Обозначим через Δs путь, пройденный за промежуток времени Δt от момента t до t + Δt , т. е.  Δs  = s(t + Δt ) - s (t). Отношение    называется средней скоростью точки за время от t до t + Δt.  

Чем меньше Δt, т. е. чем короче промежуток времени от t до t + Δt, тем лучше средняя скорость характеризует  движение точки в момент времени t. Поэтому  естественно ввести понятиескорости v в данный  момент t, определив ее как предел средней  скорости за промежуток отt до t + Δt, когда Δt→ 0:   

Величина v называется мгновенной  скоростью точки в данный момент t.  

Задача о касательной к данной кривой.  

Пусть на плоскости хОу дана кривая уравнением у = f (х). Требуется провести  касательную к данной кривой в данной точке  . 

Так как точка касания   дана, то для решения задачи потребуется найти только угловой коэффициент искомой касательной, т. е. tg φ — тангенс угла наклона касательной к  положительному направлению оси Ох (рис.). 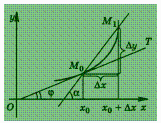 Через точки   и   проведем секущую    

Из рис. видно, что угловой коэффициент tg α секущей   равен отношению   — , где  Угловой коэффициент касательной   к  данной кривой в точке   можно найти на  основании следующего определения:  касательной к кривой в точке   называется прямая  ,  угловой коэффициент которой равен пределу углового коэффициента секущей  , когда   .  Отсюда следует, что   

11. Производная функции.Геометрич смысл,механич смысл…

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Геометрический и физический смысл производной 

Тангенс угла наклона касательной прямой 

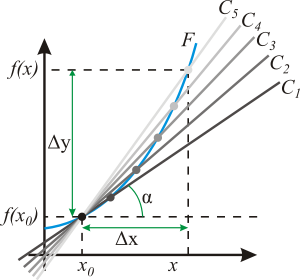
Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точкиx₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Основная статья: Касательная прямая

Если функция   имеет конечную производную в точке   то в окрестности   её можно приблизить линейной функцией

Функция   называется касательной к   в точке   Число   является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции 

Материальная точка движется по координатной прямой, причем задан закон движения, т. е. координата х этой точки есть известная функция х(t) времени t. За промежуток времени от t₀) до t₀) + Δt перемещение точки равно х (t₀) + Δt) — х (t₀)) = Δх, а ее средняя скорость такова:  При Δt<0 формула (1) также верна: перемещение равно х (t₀))—x (t₀)+Δt) = —Δх, а продолжительность промежутка времени равна -Δt. Обычно характер движения бывает таким, что при малых Δt средняя скорость практически не меняется, т. е. движение с большой степенью точности можно считать равномерным (см. пример п. 13). Другими словами, значение средней скорости при Δt→0 стремится к некоторому вполне определенному значению, которое и называют мгновенной скоростью v (t₀) материальной точки в момент времени to. Итак,

 при 

Но по определению производной

 при 

Поэтому считают, что мгновенная скорость v (t) определена (только) для любой дифференцируемой функции x(t), при этом

 (2)

Коротко говорят: производная от координаты по времени есть скорость. В этом состоит механический смысл производной.

 Скорость движения точки есть функция от времени t. А производная этой функции называется ускорением движения:

Коротко говорят: производная от скорости по времени есть ускорение.